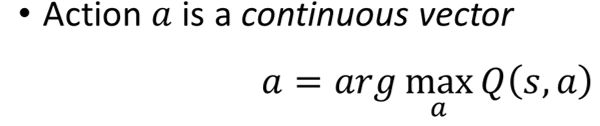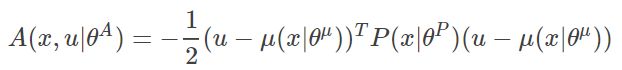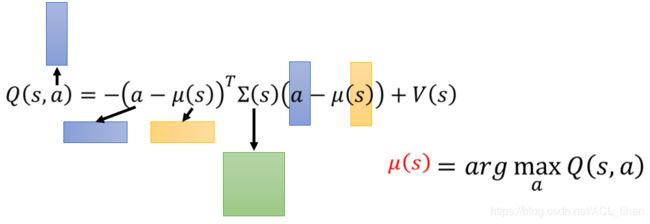【李宏毅深度强化学习笔记】5、Q-learning用于连续动作 (NAF算法)
【李宏毅深度强化学习笔记】1、策略梯度方法（Policy Gradient）
【李宏毅深度强化学习笔记】2、Proximal Policy Optimization (PPO) 算法
【李宏毅深度强化学习笔记】3、Q-learning（Basic Idea）
【李宏毅深度强化学习笔记】4、Q-learning更高阶的算法
【李宏毅深度强化学习笔记】5、Q-learning用于连续动作 (NAF算法)（本文）
【李宏毅深度强化学习笔记】6、Actor-Critic、A2C、A3C、Pathwise Derivative Policy Gradient
【李宏毅深度强化学习笔记】7、Sparse Reward
【李宏毅深度强化学习笔记】8、Imitation Learning
-------------------------------------------------------------------------------------------------------
【李宏毅深度强化学习】视频地址：https://www.bilibili.com/video/av63546968?p=5
课件地址：http://speech.ee.ntu.edu.tw/~tlkagk/courses_MLDS18.html
-------------------------------------------------------------------------------------------------------
普通的Q-learning比policy gradient比较容易实现，但是在处理连续动作（比如方向盘要转动多少度）的时候就会显得比较吃力。
因为如果action是离散的几个动作，那就可以把这几个动作都代到Q-function去算Q-value。但是如果action是连续的，此时action就是一个vector，vector里面又都有对应的value，那就没办法穷举所有的action去算Q-value。
先介绍2种容易想到但效果不一定好的方法
1、 穷举action
这个方法sample N个action，一个一个代到Q function里，看哪个a得到的Q value最大。
缺点：即便sample 很多很多个action，还是没办法把所有的action都穷举出来（因为它是连续动作）。这样就会导致结果不那么精确。
2、使用梯度上升求Q value
使用gradient ascent来求解，看采取什么action能让Q-function得到最大的Q value。
缺点：
- 由于使用gradient ascent，可能得到的结果只是局部的最优解。
- 每次考虑采取哪个a前，都要做一次类似于train network的工作，这个运算量太大
以上两种方法是比较容易想到，但是效果不好的方法，下面介绍一个比较好的方法
3、Normalized Advantage Functions（NAF）
设计一个新的网络来解连续动作的最优化问题。
论文地址：https://arxiv.org/pdf/1603.00748.pdf
先给出概念如下，后面再讲具体的。
（公式3-1）
此时Q value 由状态值函数V与动作价值函数 A 相加而得。
（公式3-2）
其中 x 表示状态State，u表示动作Action，θ 是对应的网络参数，A函数可以看成动作 u 在状态 x 下的优势。我们的目的就是要使网络输出的动作 u 所对应的Q值最大。
具体来说，如下：
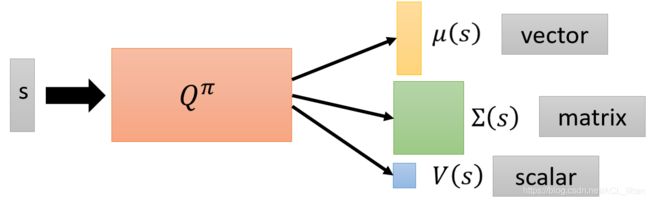
从buffer里sample一个batch的transition（
），新的Q function以状态
，动作
作为输入，依据输入的得到输出
（vector），
（matrix），
（scalar）
其中，在输出这个矩阵前，其实先输出了矩阵L，矩阵L是对角线都是正数的下三角矩阵。然后根据乔列斯基（Cholesky）分解，构造出最终的这个矩阵（对应公式3-2的P矩阵）。
输入的动作a再与上面三个结果进行组合形成Q function，如下图：
a和
转置后，变成1行N列；与矩阵相乘；与a和（N行1列）相乘，最终变成一个普通的数值，即标量（scalar），再加上
就是最后的Q value。另外，在状态s下要做出的action由给出。这样，NAF就实现既输出动作action，也输出这个action对应的Q value。
（这时候再看一下，上图的前三项其实就是类似于文章前面的公式3-1和公式3-2的A函数（优势函数）。）
接下来看如何使Q function输出的Q value达到最大值：
这是NAF的Q function：
优势函数（advantage function）可以看成
，又因为P矩阵在论文中有设定为是正定的矩阵,那么A就是一个小于等于0的值。
所以，理想的情况就是当 = a，那么此时A函数达到最大值0，那么Q function也得到最大的Q value。
可能有人疑惑：
既然是通过输出action，那输入的action是干什么的？
（这里是我参考（https://blog.csdn.net/lipengcn/article/details/81840756）后的理解，不一定准确，如果有误请提出！）
输入的action 是从transition中sample的动作，是起到训练网络中的label的作用。目的是让网络输出的不偏离 a 太多并且希望最后逐点收敛于a，从而得到最大的Q value。
下图为NAF执行过程（图参考自https://blog.csdn.net/u013236946/article/details/73243310）
NAF伪代码如下：
Normalized Advantage Functions（NAF）更多内容可参考以下博文
https://blog.csdn.net/lipengcn/article/details/81840756
https://blog.csdn.net/u013236946/article/details/73243310
https://zhuanlan.zhihu.com/p/21609472
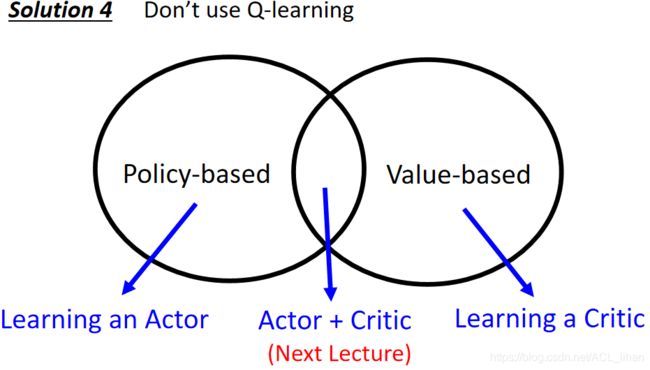
4、不使用Q-learning而使用actor-critic
具体内容可以看下篇笔记（https://blog.csdn.net/ACL_lihan/article/details/104087569）