商业数据分析实战（酒卷隆志/里洋平）——第六章案例 D—多元回归分析 如何通过各种广告的组合获得更多的用户

商业数据分析实战（酒卷隆志/里洋平）——第六章案例 D—多元回归分析如何通过各种广告的组合获得更多的用户

投放广告最优化问题
到目前为止我们已经在互联网上投放了《黑猫拼图》游戏的广告。但是为了获得更多的用户，我们决定也在传统媒体上（电视、杂志）上投放广告。基于过去其他游戏广告的数据，我们希望能够获得效果最好的广告投放方式，那么我们应该怎么做呢？

# 加载python所需模块
import pandas as pd
from scipy.stats import chi2_contingency
import pandasql
import numpy as np #之后需要用到
import seaborn as sns
import matplotlib as mpl #设置环境变量
import matplotlib.pyplot as plt #绘图专用
import statsmodels.api as sm 
from statsmodels.stats.outliers_influence import summary_table
from mpl_toolkits.mplot3d import Axes3D #绘制3D图
mpl.rcParams['font.sans-serif'] = ['FangSong']
mpl.rcParams['axes.unicode_minus']=False

现状和预期

互联网广告和传统媒体广告

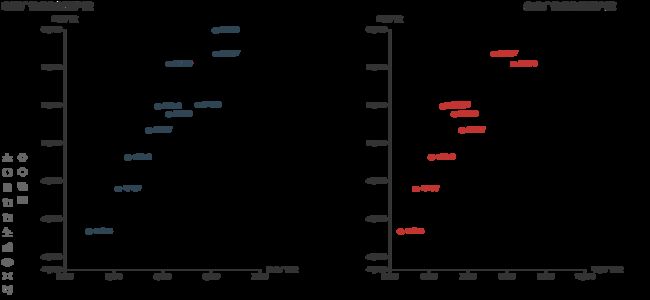
在互联网上投放广告，单价比较便宜，并且能够吸引到稳定的新注册用户。虽然互联网广告可以根据投入的成本预估效果，但相对于电视、杂志等传统媒体来说，它的受众数量是有限的，因此要想使用户达到一定数量，一般还是要在传统媒体上投放广告。然而，和互联网广告相比，传统媒体的广告成本要高得多。另外，如下图所示，根据广告投放媒体的属性不同，广告效果 CPI（Cost Per Install，获得一个新用户所需的成本）的变动也很大。

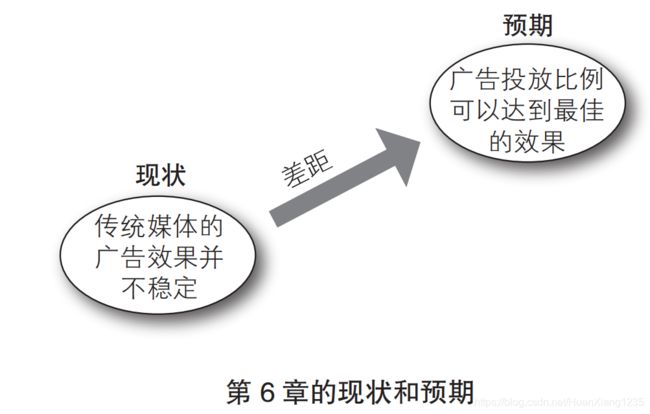
整理现状和预期

下面我们来整理一下现状和预期。首先，我们所面临的现状是广告效果 CPI 参差不齐。针对这种现状，在互联网广告方面，我们和 3 家公司保持着合作，而在传统媒体的电视和杂志上投放广告时，我们选择了一家广告公司进行合作。该广告公司建议我们，对于目前已合作的 10家左右的媒体，为了维持良好的合作关系，应避免连续 3 个月不投放广告的情况。根据这个建议，我们在各大传统媒体上都投放了广告。
　　这其中我们需要确定在电视和杂志上投放广告的合适比例（当然也可以让广告公司来替我们完成这项工作）。
　　总之，在本例中我们需要在已有合作关系的媒体中决定如何分配广告投放的比例，以达到“用较少的费用获得更多的用户”的目的。那么，基于现有的数据，我们需要弄清广告和获得用户数量之间的因果关系，并找出最合适的广告投放分配比例。下面我们先找出问题。

发现问题

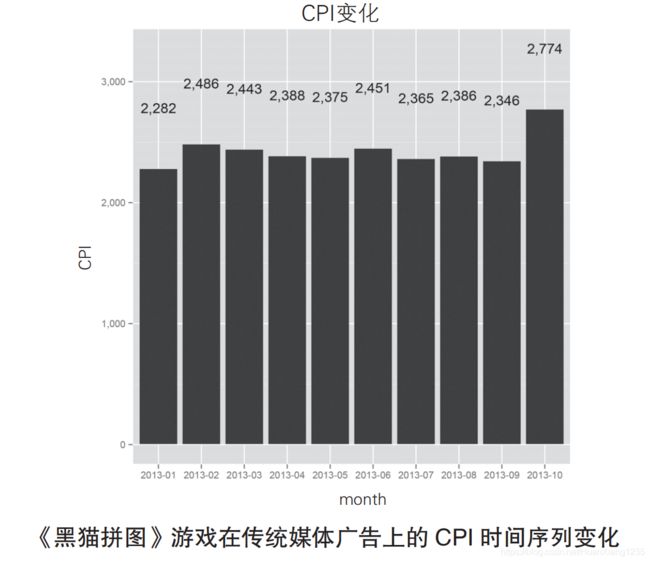
根据下图所示的广告 CPI 的变化可知，本例中的问题是每月广告CPI 的波动较大。另一方面，互联网广告每获得一个用户的成本大约在100 日元。但是，互联网广告的覆盖范围比较有限，那些不怎么接触互联网的用户，平时可能只是偶尔使用一下 Facebook 或者 LINE，对于这些用户，可以借助电视或者杂志等传统媒体提高他们对产品的认知度。
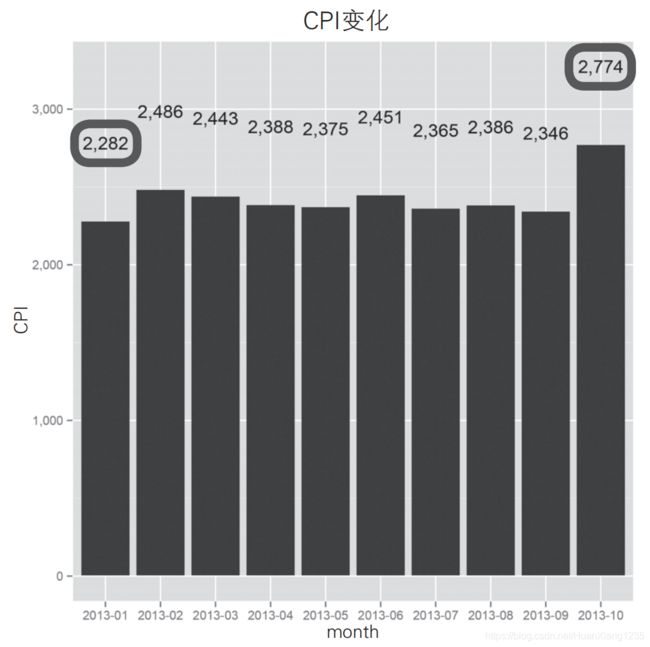
　　然而，和互联网广告不同，电视和杂志属于间接型媒体，从某个用户通过电视广告了解某个产品并产生兴趣，一直到该用户尝试购买这个产品，中间存在着一定的时间间隔。可能是受此影响，电视或者杂志广告的 CPI 高达几千日元。例如，如下图所示，传统媒体广告的月平均CPI 在 2282 日元到 2774 日元之间波动。
　　如果仅仅是看数值，读者可能会觉得月平均 CPI 的差距并不大。但由于每获得一个用户的成本都很高，因此我们要尽可能地缩小这 500 日元的差距，如果可能的话，应尽量确保 CPI 保持在 2282 日元左右。我们将本例中的问题细化如下。
　　在传统媒体上的广告投放分配比例存在问题
　　→ 每月在电视和杂志上投放广告的比例有所不同
　　通过和广告部确认，我们了解到，虽然我们无法指定投放广告的电视或杂志媒体数量，但我们可以告诉广告公司分别投放在电视和杂志上的比率，因此
　　1. 基于过去的数据，明确在电视和杂志上投放广告的广告费和各自所获得的用户数之间的关系
　　2. 基于上述关系，确定以何种比例在电视和杂志上投放广告
　　至此，我们细化了问题，并确定了分析的步骤。那么，如何对电视和杂志的广告费与各自所获得的用户数之间的关系进行建模呢？

多元回归模型的分析方法

在前面的章节中，我们介绍了“交叉列表统计”“统计学假设检验”两种用于数据间关联性分析的方法。

原因	结果
大降价	销量大
派发的传单多	来店的顾客多
来店的顾客多	销售额大

如上表所述，通过明确各自的因果关系，可以判断诸如降价和销量之间是否存在关系。但是目前的分析仍然不能回答一些更具体的问题，例如“价格下降多少能够带来多大的销量增加”。在商业领域，通常的做法是在充分考虑成本的前提下预估一个结果，再采取相应的对策。也就是说，通常我们会先确定结果，再反过来考虑相应对策的成本。放在本次案例中，我们需要先构筑一个可以预估各广告媒体能带来的用户量的模型，再决定广告的投放方式。
　　此时就需要用到“回归分析 / 多元回归分析”。回归分析的思路非常简单，可以说是交叉列表统计的扩展。我们将数据描绘在图上，每个点表示一个数据，其中横坐标表示的变量称为自变量，纵坐标表示的变量称为因变量。然后我们在图上画出一条与这些数据点最为拟合的直线，根据这条直线上任何一点的横坐标（自变量）的值就可以得到纵坐标（因变量）的值，这就是线性回归分析。
　　例如，通过交叉列表统计，可以得知广告费花得越多，相应的新增用户就会越多。接下来我们就需要考虑能否对这种关系进行建模。具体来说，就是当我们知道了广告费用的预算之后，是否能够预估出由此可能带来的新用户数量。我们以下面左边的图为例来说明，图中的横轴表示广告费，纵轴表示新用户数。

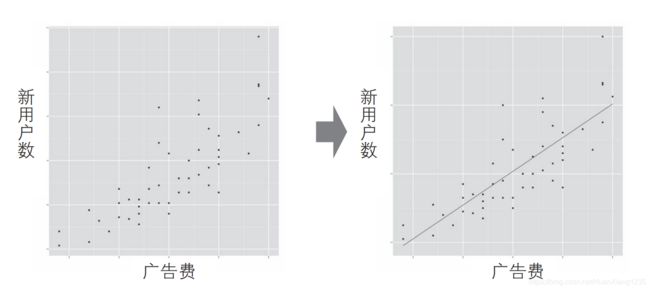
如图所示，通过观察图中的所有数据，可以发现广告费和新用户数之间果然存在一定的关系。于是我们对此进行回归分析，并对这种关系建模，如右图所示。
　　图中的这条直线就是最简单的一种模型，该直线可以用下面的公式来表述。
　　新用户数 = β× 广告费 + α
　　回归分析就是根据现有的数据来估计 α 和 β 的值。根据从回归分析的结果得出的公式和各项指标，我们进行如下分析。
　　● 原因数据真的会对结果数据产生影响吗广告费（自变量）的变化真的会对新用户数（因变量）产生影响吗
　　● 如果确实有影响，那么这是一种怎样的关系呢

数据的收集

探讨和收集分析所需的数据

到目前为止，我们在互联网、电视和杂志 3 个广告媒体上开展了商业推广活动。使用过去实际的成果数据，我们就能够对各个广告媒体的效果进行分析。
　　在这 3 个广告媒体中，由于互联网广告的效果可以直接测定，因此哪个网站的广告有什么样的效果，其 CPI 很明确。然而，关于电视和杂志广告，我们只能获取总体的用户数增加了这类粗略的信息。因此，我们排除了互联网广告所带来的新用户，将剩余的新用户数和花费在电视以及杂志上的广告费作为分析用的数据。
　　经和市场部确认得知，这些数据一直都在用 Excel 管理，因此我们只需将必要的数据存入 CSV 文件，再将其读入到分析软件中即可。

《黑猫拼图》游戏在电视和杂志上投入的广告费和所获得的新用户数

data = pd.read_csv('../../data/ad_result.csv')
data = data.rename(columns={'month':'月份',
                           'tvcm':'电视广告费',
                           'magazine':'杂志广告费',
                           'install':'新用户数',})
data.head(10)

	月份	电视广告费	杂志广告费	新用户数
0	2013-01	6358	5955	53948
1	2013-02	8176	6069	57300
2	2013-03	6853	5862	52057
3	2013-04	5271	5247	44044
4	2013-05	6473	6365	54063
5	2013-06	7682	6555	58097
6	2013-07	5666	5546	47407
7	2013-08	6659	6066	53333
8	2013-09	6066	5646	49918
9	2013-10	10090	6545	59963

数据分析

首先，我们需要确认广告和新用户数之间是否存在关系。如果二者之间的关系不那么强，就不能断言用户数量的增加是由广告带来的。我们将数据之间的关系的强弱称为“相关性”。为了确认这种相关性，一般来说首先需要观察数据的散点图。

电视、杂志的广告费和新用户数的散点图

# pip install pyecharts   pip install pyecharts_snapshot
from pyecharts import options as opts
from pyecharts.charts import Scatter, Grid

scatter1 = (
    Scatter()
    .add_xaxis(data['电视广告费'])
    .add_yaxis("", data['新用户数'])
    .set_global_opts(title_opts=opts.TitleOpts(title="电视广告费和新用户数"),
                     toolbox_opts=opts.ToolboxOpts(orient='vertical',pos_left=0,pos_top='50%'),
                     xaxis_opts=opts.AxisOpts(
                         name='电视广告费', min_=5000, max_=10000),
                     yaxis_opts=opts.AxisOpts(
                         name='新用户数', min_=41000, max_=60000))
)
scatter2 = (
    Scatter()
    .add_xaxis(data['杂志广告费'])
    .add_yaxis("", data['新用户数'])
    .set_global_opts(title_opts=opts.TitleOpts(title="杂志广告费和新用户数",pos_right='5%'),
                     xaxis_opts=opts.AxisOpts(
                         name='杂志广告费', min_=5000, max_=7000),
                     yaxis_opts=opts.AxisOpts(
                         name='新用户数', min_=41000, max_=60000))
)
grid = (
    Grid(init_opts=opts.InitOpts(width='1300px', height='600px'))
    .add(scatter1, grid_opts=opts.GridOpts(pos_left="60%"))
    .add(scatter2, grid_opts=opts.GridOpts(pos_right="60%"))
)
grid.render_notebook()

无论是电视广告还是杂志广告，从散点图来看，随着投入的广告费用的增加，新获得的用户数也会增加，反应在图上就是数据点不断地向右上方延伸。既然明确了广告费和新用户数之间存在关系，下面我们就来着手进行回归分析。

进行多元回归分析

x = data.loc[:,['电视广告费','杂志广告费']]
y = data['新用户数']
x2 = sm.add_constant(x)
est = sm.OLS(y,x2)
est2 = est.fit()
est2.summary()

D:\programs\Anaconda3\envs\python3.6.5\lib\site-packages\scipy\stats\stats.py:1604: UserWarning: kurtosistest only valid for n>=20 ... continuing anyway, n=10
  "anyway, n=%i" % int(n))

OLS Regression Results

Dep. Variable:	新用户数	R-squared:	0.938
Model:	OLS	Adj. R-squared:	0.920
Method:	Least Squares	F-statistic:	52.86
Date:	Mon, 22 Jun 2020	Prob (F-statistic):	5.97e-05
Time:	22:31:50	Log-Likelihood:	-84.758
No. Observations:	10	AIC:	175.5
Df Residuals:	7	BIC:	176.4
Df Model:	2
Covariance Type:	nonrobust

	coef	std err	t	P>|t|	[0.025	0.975]
const	188.1743	7719.131	0.024	0.981	-1.81e+04	1.84e+04
电视广告费	1.3609	0.517	2.630	0.034	0.137	2.584
杂志广告费	7.2498	1.693	4.283	0.004	3.247	11.252

Omnibus:	0.992	Durbin-Watson:	0.881
Prob(Omnibus):	0.609	Jarque-Bera (JB):	0.795
Skew:	0.534	Prob(JB):	0.672
Kurtosis:	2.124	Cond. No.	1.63e+05

Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 1.63e+05. This might indicate that there are
strong multicollinearity or other numerical problems.

● 多元回归模型的系数

params = pd.DataFrame(est2.params).rename(columns={0:'系数'})
params

	系数
const	188.174275
电视广告费	1.360921
杂志广告费	7.249809

根据上表的输出结果，我们可以得到下述关系。
　　新用户数 = 1.361 × 电视广告费 + 7.250 × 杂志广告费 + 188.174
　　从上式可以看出，如果不投放广告，则每月新增的用户数为大约188 人。如果在电视广告上投入 1 日元，就能够获得 1 名新用户。在杂志广告上投入 1 日元，则可获得 7 名新用户。也就是说，通过杂志广告来获得新用户的效率要远远高于电视广告。

对多元回归模型的详细探讨

对于上面的模型公式，我们再做进一步探讨。

① 残差的分布

#获取各个y值的残差
data_dict = {}
yt, data1, ss2 = summary_table(est2, alpha=0.05) # 置信水平alpha=5%，st数据汇总，data1数据详情，ss2数据列名
Residual = data1[:,8]
data_dict['最小值'] = np.min(Residual)
data_dict['第 1 四分位数'] = np.quantile(Residual,0.25)
data_dict['中值'] = np.quantile(Residual,0.5)
data_dict['第 3 四分位数'] = np.quantile(Residual,0.75)
data_dict['最大值'] = np.max(Residual)
data_dict = pd.DataFrame([data_dict])
data_dict

	最小值	第 1 四分位数	中值	第 3 四分位数	最大值
0	-1406.871108	-984.488813	-12.109952	432.818096	1985.841421

残差（预测值和实际值之差）的分布用四分位数的方式来表示，据此可以判断数据是否存在异常偏差。

② 多元回归模型的系数

df = pd.DataFrame({'预估值':est2.params
                  ,'标准误差': est2.tvalues
                  ,'t值': est2.pvalues
                  ,'p值': est2.bse}
                 )

df

	预估值	标准误差	t值	p值
const	188.174275	0.024378	0.981232	7719.130841
电视广告费	1.360921	2.630156	0.033905	0.517430
杂志广告费	7.249809	4.283126	0.003641	1.692644

上表总结了预估得到的常数项和斜率等数据。每一行的数据分别是预估值、标准误差、t 值、p 值，据此可以得知每个属性相应的斜率是多少，以及是否具有统计学意义。

③ 判定系数和自由度校正判定系数

判定系数：0.938，自由度校正判定系数：0.92
　　判定系数越接近于 1，表示这个模型拟合得越好。
　　观察①中的残差分布，我们发现，第 1 四分位数的绝对值要大于第3 四分位数的绝对值，这说明某些数据点的分布存在偏差，但由于③中自由度校正判定系数的值较高，因此现在的广告投放策略应该是没有问题的。

解决对策

本例中我们围绕如下问题进行了分析。
　　1. 通过各种传统媒体广告所获得的新用户数不尽相同 （事实）
　　2. 每月获得的新用户数与在电视和杂志上的广告投放比例相关（假设）
　　3. 把握电视广告费和杂志广告费各自与获得的新用户数之间的关系
　　4. 基于这种关系，确定一个最佳的广告分配比例
　　基于上述问题设定，我们使用多元回归分析推导出了传统媒体广告和新用户数之间的关系，如下所示。
　　新用户数 = 1.361× 电视广告费 + 7.250× 杂志广告费 + 188.174
　　从上式可以看出，相比于电视广告，杂志广告的效果要更好一些。即便采取只投放杂志广告而不投放电视广告的极端行为，效果也不会太差。但是上述公式毕竟只是基于本例中的数据计算得出的，对于超出本 例数据范围的值则不适用。
　　另外，如前所述，为了维持和广告公司的合作关系，我们不会对任何一家广告媒体连续 3 个月不投放任何广告。
　　因此，这回我们将按照下述比例来分配广告费用。
　　电视广告：4200 万日元
　　杂志广告：7500 万日元
　　根据上面的计算公式，我们可以得到如下结果。
　　60279 人 = 1.361×（4200 万日元） + 7.250 ×（7500 万日元）+ 188.174
　　也就是说，我们预期可以获得大约 6 万的新用户。

小结

本章介绍了数据分析中的多元回归分析。
　　对于那些成本较高的问题，该方法可用于最优化其效益成本比。尤其在商业领域，大家一般都更关注成本较高的事情，哪怕只提升了少许的效果，对于整体来说也可能起到很大的作用。这种情况下最适合使用多元回归分析，该方法能够预测出每种策略应该占多大比重。
　　在事前能预测大部分结果，且在实施阶段需要耗费高成本的情况下，多元回归分析是不二的选择。

分析流程	第6章中数据分析的成本
现状和预期	低
发现问题	低
数据的收集和加工	低
数据分析	中
解决对策	低

注：

   本文文字内容主要来源于书籍：《数据分析实战》 [日] 酒卷隆志 里洋平/著 肖峰/译
   本文代码是自己手打的
   本文github地址：https://github.com/qq1044645270/data_analysis