Astar A*算法 最短路径算法

通常情况下，迷宫寻路算法可以使用深度优先或者广度优先算法，但是由于效率的原因，不会直接使用这些算法，在路径搜索算法中最常见的就是A*寻路算法。使用A*算法的魅力之处在于它不仅能找到地图中从A到B的一条路径，还能保证找到的是一条最短路径，它是一种常见的启发式搜索算法，类似于Dijkstra算法一样的最短路径查找算法，很多游戏应用中的路径搜索基本都是采用这种算法或者是A*算法的变种。

下面我们来了解一下A*算法相关的理论知识：

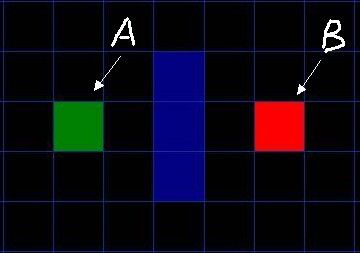
如图，我们需要在迷宫中找到A点到B点的一条最短的可以通过的路径，A和B直接被一面墙堵住了。在上一篇博客中我们说到了，地图是有二维数组组成的，墙表示不能通过的地方，用1表示，A*算法所要做的就是从A找到一条最短的通向B的路径。当然，不能从墙上飞过去，也不能瞬移到B。只能每次移动一个格子，一步一步地移动到B目标位置。问题在于，每次移动一格的时候，有上下左右四个方向，这里我们限制物体斜向移动，如何选择下一个移动方向呢？按照我们的想法，不就是找一条离目标最近的路吗？那我们可以在这四个方向中，找一个最接近目标点的位置，当然，还要考虑障碍因素，基于这个思想，A*算法采用了以下的搜索步骤来实现：

　　1.首先把起始位置点加入到一个称为“open List”的列表，在寻路的过程中，目前，我们可以认为open List这个列表会存放许多待测试的点，这些点是通往目标点的关键，以后会逐渐往里面添加更多的测试点，同时，为了效率考虑，通常这个列表是个已经排序的列表。

　　2.如果open List列表不为空，则重复以下工作：

　　（1）找出open List中通往目标点代价最小的点作为当前点；

　　（2）把当前点放入一个称为close List的列表；

　　（3）对当前点周围的4个点每个进行处理（这里是限制了斜向的移动），如果该点是可以通过并且该点不在close List列表中，则处理如下；

　　（4）如果该点正好是目标点，则把当前点作为该点的父节点，并退出循环，设置已经找到路径标记；

　　（5）如果该点也不在open List中，则计算该节点到目标节点的代价，把当前点作为该点的父节点，并把该节点添加到open List中；

　　（6）如果该点已经在open List中了，则比较该点和当前点通往目标点的代价，如果当前点的代价更小，则把当前点作为该点的父节点，同时，重新计算该点通往目标点的代价，并把open List重新排序；

　　3.完成以上循环后，如果已经找到路径，则从目标点开始，依次查找每个节点的父节点，直到找到开始点，这样就形成了一条路径。 

 

　　以上，就是A*算法的全部步骤，按照这个步骤，就可以得到一条正确的路径。这里有一个关键的地方，就是如何计算每个点通往目标点的代价，之所以称为A*算法为启发式搜索，就是因为通过评估这个代价值来搜索最近的路径，对于任意一个点的代价值，在A*算法中通常使用下列的公式计算：

代价F=G+H

　　在这里，F表示通往目标点的代价，G表示从起始点移动到该点的距离，H则表示从该点到目标点的距离，比如图中，可以看到小狗的附近格子的代价值，其中左上角的数字代表F值，左下角的数字代表G值，右下角的数字代表H值。拿小狗上方的格子来举例，G=1，表示从小狗的位置到该点的距离为1个格子，H=6，表示从小狗到骨头的距离是6个格子，则F=G+H=7。在此处，距离的算法是采用曼哈顿距离，它计算从当前格子到目的格子之间水平和垂直的方格的数量总和，例如在平面上，坐标（x1,y1）的点和坐标（x2,y2）的点的曼哈顿距离为：

|x1-x2|+|y1-y2|

当然，距离的算法也可以采用其他的方法，实际在游戏中，这个移动的代价除了要考虑距离因素外，还要考虑当前格子的游戏属性。比如有的格子表示水路、草地、陆地，这些有可能影响人物移动的速度，实际计算的时候还要把这些考虑在内。

　　另一个需要注意的就是，在计算这个距离的时候是毋须考虑障碍因素的，因为在以上A*算法步骤中会剔除掉障碍。

　　这样，按照前面所说的A*算法的步骤，第一次循环open List的时候，把A点作为当前点，同时把A周围的四个点放入到open List中。第二次循环的时候把A右边的点作为当前点，该点的父节点就是A，这是处理当前点的时候，只需要把当前点的上下两个点放入open List中，因为左边的A已经在close List中，而右边的是墙，所以直接被忽略。

伪代码：

 

具体例子：

 

代码：

astar.h

#ifndef ASTAR_H
#define ASTAR_H

#include 
#include 
#include 

namespace AStar
{
    struct Vec2i
    {
        int x, y;
        bool operator == (const Vec2i& coordinates_);
    };

    using uint = unsigned int;
    using HeuristicFunction = std::function;
    using CoordinateList = std::vector;

    struct Node
    {
        uint G, H;
        Vec2i coordinates;
        Node *parent;

        Node(Vec2i coord_, Node *parent = nullptr);
        uint getScore();
    };

    using NodeSet = std::set;

    class Generator
    {
        // default private
        bool detectCollision(Vec2i coordinates_);
        Node* findNodeOnList(NodeSet &nodes_, Vec2i coordinates_);
        void releaseNodes(NodeSet &nodes_);

    public:
        Generator();
        void setWorldSize(Vec2i worldSize_);
        void setDiagonalMovement(bool enable_);
        void setHeuristic(HeuristicFunction heuristic_);
        CoordinateList findPath(Vec2i source_, Vec2i target_);
        void addCollision(Vec2i coordinates_);
        void removeCollision(Vec2i coordinates_);
        void clearCollision();

    private:
        HeuristicFunction heuristic;
        CoordinateList direction, walls;
        Vec2i worldSize;
        uint directions;
    };

    class Heuristic
    {
    private:
        static Vec2i getDelta(Vec2i source_, Vec2i target_);

    public:
        static uint manhattan(Vec2i source_, Vec2i target_);
        static uint euclidean(Vec2i source_, Vec2i target_);
        static uint octagonal(Vec2i source_, Vec2i target_);
    };
}

#endif // ASTAR_H

 

astar.cpp

#include "astar.h"
#include 

using namespace std::placeholders;

bool AStar::Vec2i::operator == (const Vec2i &coordinates_)
{
    return (x == coordinates_.x && y == coordinates_.y);
}

AStar::Vec2i operator + (const AStar::Vec2i& left_, const AStar::Vec2i& right_)
{
    return { left_.x + right_.x, left_.y + right_.y };
}

AStar::Node::Node(Vec2i coordinates_, Node *parent_)
{
    parent = parent_;
    coordinates = coordinates_;
    G = H = 0;
}

AStar::uint AStar::Node::getScore()
{
    return G + H;
}

AStar::Generator::Generator()
{
    setDiagonalMovement(false);
    setHeuristic(&Heuristic::manhattan);
    direction = {
        { 0, 1 }, { 1, 0 }, { 0, -1 }, { -1, 0 },
        { -1, -1 }, { 1, 1 }, { -1, 1 }, { 1, -1 }
    };
}

void AStar::Generator::setWorldSize(Vec2i worldSize_)
{
    worldSize = worldSize_;
}

void AStar::Generator::setDiagonalMovement(bool enable_)
{
    directions = (enable_ ? 8 : 4);
}

void AStar::Generator::setHeuristic(HeuristicFunction heuristic_)
{
    heuristic = std::bind(heuristic_, _1, _2);
}

void AStar::Generator::addCollision(Vec2i coordinates_)
{
    walls.push_back(coordinates_);
}

void AStar::Generator::removeCollision(Vec2i coordinates_)
{
    auto it = std::find(walls.begin(), walls.end(), coordinates_);
    if (it != walls.end()) {
        walls.erase(it);
    }
}

void AStar::Generator::clearCollision()
{
    walls.clear();
}

/* key function */
AStar::CoordinateList AStar::Generator::findPath(Vec2i source_, Vec2i target_)
{
    Node *current = nullptr;
    NodeSet openSet, closedSet;
    openSet.insert(new Node(source_));

    while (!openSet.empty())
    {
        current = *openSet.begin();
        for (auto node : openSet) {
            if (node->getScore() <= current->getScore()) {
                current = node;
            }
        }
        if (current->coordinates == target_) {
            break;
        }

        closedSet.insert(current);
        openSet.erase(std::find(openSet.begin(), openSet.end(), current));

        for (uint i = 0; i < directions; ++i) {
            Vec2i newCoordinates(current->coordinates + direction[i]);
            if (detectCollision(newCoordinates) ||
                findNodeOnList(closedSet, newCoordinates)) {
                continue;
            }

            uint totalCost = current->G + ((i < 4) ? 10 : 14);

            Node *successor = findNodeOnList(openSet, newCoordinates);
            if (successor == nullptr) {
                successor = new Node(newCoordinates, current);
                successor->G = totalCost;
                successor->H = heuristic(successor->coordinates, target_);
                openSet.insert(successor);
            }
            else if (totalCost < successor->G) {
                successor->parent = current;
                successor->G = totalCost;
            }
        }
    }
    CoordinateList path;
    while (current != nullptr) {
        path.push_back(current->coordinates);
        current = current->parent;
    }

    releaseNodes(openSet);
    releaseNodes(closedSet);

    return path;
}

AStar::Node* AStar::Generator::findNodeOnList(NodeSet& nodes_, Vec2i coordinates_)
{
    for (auto node : nodes_) {
        if (node->coordinates == coordinates_) {
            return node;
        }
    }
    return nullptr;
}

void AStar::Generator::releaseNodes(NodeSet& nodes_)
{
    for (auto it = nodes_.begin(); it != nodes_.end();) {
        delete *it;
        it = nodes_.erase(it);
    }
}

bool AStar::Generator::detectCollision(Vec2i coordinates_)
{
    if (coordinates_.x < 0 || coordinates_.x >= worldSize.x ||
        coordinates_.y < 0 || coordinates_.y >= worldSize.y ||
        std::find(walls.begin(), walls.end(), coordinates_) != walls.end()) {
        return true;
    }
    return false;
}

AStar::Vec2i AStar::Heuristic::getDelta(Vec2i source_, Vec2i target_)
{
    return{ abs(source_.x - target_.x),  abs(source_.y - target_.y) };
}

AStar::uint AStar::Heuristic::manhattan(Vec2i source_, Vec2i target_)
{
    auto delta = std::move(getDelta(source_, target_));
    return static_cast(10 * (delta.x + delta.y));
}

AStar::uint AStar::Heuristic::euclidean(Vec2i source_, Vec2i target_)
{
    auto delta = std::move(getDelta(source_, target_));
    return static_cast(10 * sqrt(pow(delta.x, 2) + pow(delta.y, 2)));
}

AStar::uint AStar::Heuristic::octagonal(Vec2i source_, Vec2i target_)
{
    auto delta = std::move(getDelta(source_, target_));
    return 10 * (delta.x + delta.y) + (-6) * std::min(delta.x, delta.y);
}

 

main.cpp

#include 
#include "astar.h"
#include 
using namespace std;
int main()
{
    AStar::Generator generator;
    generator.setWorldSize({11, 6});
    generator.setHeuristic(AStar::Heuristic::euclidean);
    generator.setDiagonalMovement(true);

    std::cout << "Generate path ... \n";
    vector> arr = {{3, 1},
                               {3, 2},
                               {4, 2},
                               {5, 2},
                               {6, 2},
                               {7, 2}};
    AStar::Vec2i colli;
    for (size_t i = 0; i < arr.size(); ++i) {
        colli.x = arr[i][0];
        colli.y = arr[i][1];
        generator.addCollision(colli);
    }

    auto path = generator.findPath({7, 4}, {4, 1});

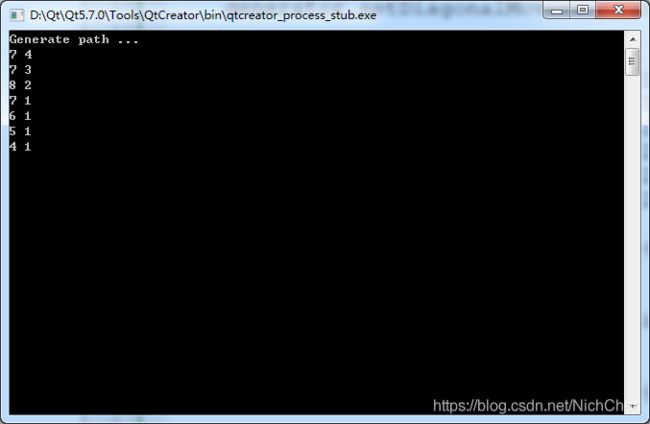
    for(int i = path.size() - 1; i >= 0; --i) {

        std::cout << path[i].x << " " << path[i].y << "\n";
    }
}

运行结果：

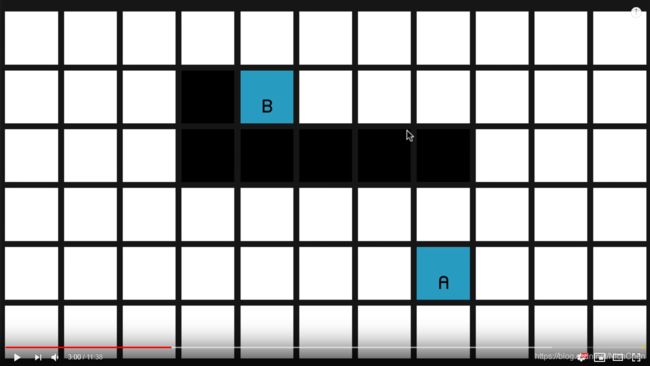
实际结果：（代码求解与实际结果一致）

 

注：

• A*算法是一种启发式算法，它的启发作用（在扩展路径时让路径点与start和target之间的距离之和最小）使得其性能比BFS和DFS来寻找最短路径更优
• A*算法由于保持了启发作用，相当于有一股外力在让start和target之间的路径趋向于最短化，因此，在这种启发下逐步搜寻处的路径，一定是最短路径（用曼哈顿距离作为启发距离则很容易理解，因为在后面从inList中选择点时，是选择的F值最小的点，若是曼哈顿距离，则在任意路径中，F都是一个非减函数，因此每次选择最小的F值比为最优值，即最短路径）

 

参考资料：

https://www.youtube.com/watch?v=-L-WgKMFuhE

https://github.com/daancode/a-star

http://www.cnblogs.com/msxh/p/5674417.html