遇到一个想做的功能,但是实现不了,核心原因是因为对U3D的3D数学概念没有灵活吃透。故再次系统学习之—第三次学习3D数学.
本次,希望实现的功能很简单:
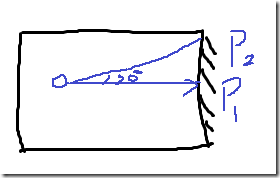
如在小地图中,希望可以动态画出Player当前的位置、z的朝向:用3条线、z轴正向、30°旋转、-30°旋转。
问题是:0点可以获得,P1点? P2点是未知的。
我尝试了2个小时,结果不竟如人意,少于沮丧。
不得不,再次花点时间系统的学习3D数学:
1 位移–向量和点:
点: 点和向量在数学上是一致的,实际生活中点的概念比较好理解,坐标点来定位–南二环、北二环。 【点用(3,4,5)圆括号来标示,简称P】
向量:“俗称增量”,有大小和方向,如”往前1步走。 左转90度”. 往前走,直到碰到墙,你才会停下来—在这之前,你无法准确获得碰到墙的点的坐标或者你和墙的距离。 【向量用<3,4,5>尖括号来标示,简称V】
在U3D中,统一用Vector3对象来表达向量和点,这个也是导致新手晕头转向的一个很重要的原因; 一个技巧,凡是在API中用position、Point的,V3肯定代表是点;凡是Vector、direction的是向量;多看官方的API手册,写得很明白。
做个游戏,列表出你用过的Vector3的API,分析分析用到的Vector3是向量(V)还是点(P)
需求 |
API |
向量(V) 点(P) |
备注 |
平滑位移 |
Vector3 MoveTowards(Vector3 current, Vector3 target, float maxDistanceDelta); |
P |
|
平滑位移 |
Vector3 Slerp(Vector3 from, Vector3 to, float t) |
P |
|
新的坐标点 |
this.m_transform.position = pos; |
P |
符合常规思维 |
变动一次坐标 |
m_transform.Translate(new Vector3(rx, 0, -m_Speed * Time.deltaTime)); |
V |
可认为是增量 |
求方向 |
Vector3 relativePos = this.m_transform.position – m_Player.position; |
V |
向量减法,较难理解 |
设置新坐标点 |
lineRenderer.SetPosition(0,this.gameObject.transform.position); m_NavAgent.SetDestination(this.m_Player.transform.position); |
P |
符合常规思维 |
新的位置 |
pointer.transform.position = hitInfo.point + (transform.position – hitInfo.point) * 0.01f; |
P、V |
力的叠加? |
求距离 |
float dis = Vector3.Distance(v1, v2); float f1 = (v1 – v2).sqrMagnitude; float f3 = (v1 – v2).magnitude; |
P、V |
Distance用点即可 向量减法也可以 |
缩放正向 |
Vector3 v3 = this.m_transform.forward * 200f; |
V |
V的数乘 |
射线检测 |
Ray r = new Ray(source, dest); Physics.Raycast(r, out hit, 1000, m_ShootMask) |
V、P |
Source:P Dest:V |
加一个力 |
rigidbody.AddForce (0, 10, 0); |
V |
依据这个游戏,可以整理出目前用到的有4个组件(含Vector 3)会发生位移:
位移常用的4个组件和Vector3:
组件 |
函数 |
Unity 圣典的API说明 |
是否 用过 |
transform组件 |
translate函数 |
向某方向移动物体多少距离【默认local坐标系】 或者相对某物体移动 |
yes |
Position属性 |
在世界空间坐标transform的位置 |
Yes |
|
RigidBody组件 [FixedUpdate函数] |
Velocity属性 |
刚体的速度向量 Unity 官方demo Done用的很酷 |
Yes |
AddForce函数 |
添加一个力到刚体。作为结果刚体将开始移动。 |
yes |
|
MovePosition函数 |
移动刚体到position |
||
NavMeshAgent组件 |
SetDestination函数 |
设置自动Path目标点 |
yes |
CharacterController 组件 |
Move函数 |
一个更加复杂的运动函数,每次都绝对运动 |
yes |
SimpleMove函数 |
以一定的速度移动角色 |
||
Vector3向量 |
Lerp函数 |
两个向量之间的线性插值。 “像弹簧一个跟随目标物体” |
|
Slerp函数 |
球形插值在两个向量之间 “在日出和日落之间动画弧线” |
||
MoveToward函数 |
当前的地点移向目标 和Vector3.Lerp相同,maxDistanceDelta限速 |
||
SmoothDamp 函数 |
随着时间的推移,逐渐改变一个向量朝向预期的目标。 |
我的几个向量相关的问题:
如何判断A向量和B向量是否同方向?
如何判断A向量和B向量前、后、左、右?
如何判断A向量和B向量的夹角?
向量的减法貌似比加法更有用一些?
Vector.Forward和this.transform.Forward都表达local坐标系,那么数值为什么不一样呢?
2 旋转–Quaternion、eulerAngles、Quaternion.Euler
旋转在3D中是比较复杂的,在Unity 3D中一般用Quaternion来进行旋转, 旋转仅涉及向量的概念(向量的方向),请思考对于坐标点或者零向量旋转有无意义?
而按照Unity 3D API官方的说法,仅有约7个方法或者操作符比较常用,且占99%的概率,我截止目前还没有用到这么多,我用到的Quaterniong约有4个函数。
旋转常用7个API:
Quaternion API |
Unity 圣典的API说明 |
是否 用过 |
Quaternion.LookRotation |
创建一个旋转,沿着forward(z轴)并且头部沿着upwards(y轴)的约束注视。也就是建立一个旋转,使z轴朝向y轴朝向up。 常用的是transform.LookAt |
yes |
Quaternion.Angle |
返回a和b两者之间的角度。 |
|
Quaternion.Euler |
返回一个旋转角度,绕z轴旋转z度,绕x轴旋转x度,绕y轴旋转y度(像这样的顺序)。 |
yes |
Quaternion.Slerp |
球形插值,通过t值from向to之间插值。 |
|
Quaternion.FromToRotation |
从fromDirection到toDirection创建一个旋转。 |
|
Quaternion.identity |
返回恒等式旋转(只读)。这个四元数对于“无旋转”:这个物体完全对齐于世界或父轴。 |
yes |
Quaternion.operator * |
由另一个四元数来旋转一个旋转角度,或由一个旋转角度来旋转一个向量 |
yes |
我的几个旋转相关的问题:
1 Quaternion.LookRotation和Vector3.RotateTowards的区别?
2 Quaternion.Angle和Vector3.Angle的区别?
3 Quaternion.LookRotation和transform.LookAt的区别?
[官方回答: 大多数时间你可以使用transform.LookAt代替
Quaternion.LookRotation]
4 如何实现2个GameObject face to face,即Z轴相对?
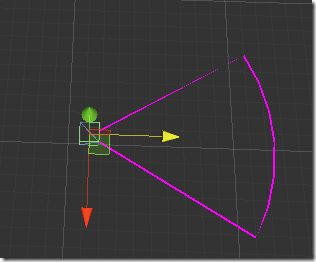
磨刀不误砍柴工: 经过一周的复习、反复验证,果然在系统学习3D 数学后,要实现的功能可以了,如下:
参考博客:
坐标系的简介:C#程序员整理的Unity 3D笔记(八):Unity 3D坐标系介绍
宣雨松的博客:http://www.xuanyusong.com/archives/1977
总结:
据说80%、90%Unity 3D程序员是自学的,大多数是看看书、实战视频、源码分析;而科班出生的同学会有3D数学这门核心课–估计占一个学期、会有作业等。为了赶上科班同学的水平,花点时间,补补数学知识,会使得自己少走一些弯路。一句话:”3D数学模型很关键。“