数据结构 栈、队列、链表与数组

1.1 数据结构中的一些概念

• 数据结构是什么
  • 简单来说，数据结果就是设计数据以何种方式存储在计算机中
  • 比如：列表，集合，与字典等都是一种数据结构
  • 程序 = 数据结构 + 算法
• 数据结构与数据类型
  • 数据类型

    • 说明：数据类型是一个值的集合和定义在此集合上一组操作（通常是增删改查或者操作读写的方法）的总称

    • 数据类型：int、str、boolean、byte

  • 数据结构

    • 说明：数据以什么方式构成，如何进行存储（数据结构是数据类型中的一种：结构类型）

    • 数据结构：数组、栈、队列、链表、树、图、堆、散列表等

    • python数据结构：列表、集合、字典、元祖

• 数据结构与数据类型比较

  • 数据类型的分类为：原子类型 和 结构类型；

  • 原子类型 = 一种值的集合 + 定义在值集合上的一组操作。（比如：python中的int，float，字符串）

  • 结构类型 = 一种数据结构 + 定义在这种数据结构上的一组操作。（比如：python中的列表，字典，元组）
    原子类型 + 结构类型 = 数据类型
    

1.2 栈（stack）

• 栈的定义
  • 栈是一种数据集合，可以理解为只能在一端进行插入或删除操作的列表
• 栈的特点
  • 后进先出（last-in, first-out）
• 栈的概念
  • 栈顶，栈底
• 栈的基本操作

  • 进栈（压栈）：push

  • 出栈：pop

  • 取栈顶：gettop

• python实现栈功能

#! /usr/bin/env python
# -*- coding: utf-8 -*-
class Stack(object):

    def __init__(self):
        self.stack = []              # 初始化一个栈

    def push(self,item):             # 入栈
        self.stack.append(item)

    def gettop(self):                # 获取栈顶元素
        return self.stack[-1]

    def pop(self):                   # 出栈
        return self.stack.pop()


if __name__ == '__main__':
    s = Stack()
    s.push(1)
    s.push(2)
    print(s.stack)

• 栈的使用：匹配括号是否成对出现

def check_kuohao(s):
   stack = []
   for char in s:
      if char in ['(','[','{']:
         stack.append(char)
      elif char == ')':
         if len(stack)>0 and stack[-1] == '(':
            stack.pop()
         else:
            return False
      elif char == ']':
         if len(stack) > 0 and stack[-1] == '[':
            stack.pop()
         else:
            return False
      elif char == '}':
         if len(stack) > 0 and stack[-1] == '{':
            stack.pop()
         else:
            return False
   if len(stack) == 0:
      return True
   else:
      return False
print(check_kuohao('(){}{}[]'))  #True

1.3 队列

• 队列定义
  • 队列是一个数据集合，仅允许在列表的一端进行插入，另一端进行删除
  • 插入的一端称为队尾（rear），插入动作叫进队或入队
  • 进行删除的一端称为对头（front），删除动作称为出队
  • 队列性质：先进先出（First-in, First-out）
  • 双向队列：队列的两端都允许进行进队和出队操作
• 对列使用方法
  • 导入： from collectios import deque
  • 创建队列：queue = deque(li)
  • 进队： append
  • 出队： popleft
  • 双向队列队首进队：appendleft
  • 双向队列队尾出队：pop
• python操作队列queue

from queue import Queue
#1. 基本FIFO队列  先进先出 FIFO即First in First Out,先进先出
#2. maxsize设置队列中，数据上限，小于或等于0则不限制，容器中大于这个数则阻塞，直到队列中的数据被消掉
q = Queue(maxsize=0)

#3. 写入队列数据
q.put(0)
q.put(1)
q.put(2)

#4. 输出当前队列所有数据
print(q.queue)

#5. 删除队列数据，并返回该数据
q.get()

#6. 输也所有队列数据
print(q.queue)

• 队列应用场景

  • 队列主要的功能是在多个进程间共享数据，实现业务解耦，提高效率

  • 生产者线程只需要把任务放入队列中，消费者线程只需要到队列中取数据进行处理

• 队列与列表区别
  • 列表中数据虽然是排列的，但数据被取走后还会保留，而队列中这个容器的数据被取后将不会保留

1.4 链表

• 单链表
  • 链表中每个元素都是一个对象，每个对象称为一个节点，包含有数据域key和指向下一节点的指针next，通过各个节点间的相互连接，最终串联成一个链表
    
  • python模拟链表数据类型

class Node(object):
    def __init__(self, item,next=None):
        self.item = item
        self.next = next
l = Node(1,Node(2,Node(3,Node(4))))
print(l.item)
print(l.next.item)

• 单链表增删改查

#! /usr/bin/env python
# -*- coding: utf-8 -*-
class Node(object):
    def __init__(self, item):
        self.item = item
        self.next = None


class DLinkList(object):
    def __init__(self):
        self._head = None

    def is_empty(self):
        return self._head == None

    def append(self, item):
        '''尾部追加元素'''
        node = Node(item)
        if self.is_empty():
            self._head = node
        else:
            cur = self._head
            while cur.next != None:
                cur = cur.next
            cur.next = node

    def add(self, item):
        """头部插入元素"""
        node = Node(item)
        if self.is_empty():
            self._head = node         # 如果是空链表，将_head指向node
        else:
            node.next = self._head      # 将node的next指向_head的头节点
            self._head = node        # 将_head 指向node

    def travel(self):
        cur = self._head
        while cur != None:
            print cur.item,
            cur = cur.next
        print ""

    def remove(self, item):
        """删除元素"""
        if self.is_empty():
            return
        else:
            cur = self._head
            if cur.item == item:
                # 如果首节点的元素即是要删除的元素
                if cur.next == None:  # 如果链表只有这一个节点
                    self._head = None
                else:  # 将_head指向第二个节点
                    self._head = cur.next
                return
            while cur != None:
                if cur.next.item == item:
                    cur.next = cur.next.next
                    break
                cur = cur.next

    def insert(self, pos, item):
        """在指定位置添加节点"""
        if pos <= 0:
            self.add(item)
        elif pos > (self.length() - 1):
            self.append(item)
        else:
            node = Node(item)
            cur = self._head
            count = 0
            # 移动到指定位置的前一个位置
            while count < (pos - 1):
                count += 1
                cur_next = cur.next
            # 将node的next指向cur的下一个节点
            cur.next = node
            node.next = cur_next

    def length(self):
        """返回链表的长度"""
        cur = self._head
        count = 0
        while cur != None:
            count += 1
            cur = cur.next
        return count


if __name__ == '__main__':
    ll = DLinkList()
    # 1、将链表后面追加三个元素：1,2,3
    ll.append(1)
    ll.append(2)
    ll.append(3)
    ll.travel()  # 1 2 3

    # 2、将链表头部插入一个元素：0
    ll.add(0)
    ll.travel()  # 1 2 3  ==>  0 1 2 3

    # 3、删除链表中的元素：3
    ll.remove(3)
    ll.travel()  # 0 1 2 3  ==>  0 1 2

    # 4、在链表的第2号位置插入元素：8
    ll.insert(2,8)
    ll.travel()  # 0 1 2  ==>  0 8 1 2 

• 链表反转

#! /usr/bin/env python
# -*- coding: utf-8 -*-
class Node(object):
    def __init__(self, val):
        self.val = val
        self.next = None

def list_reverse(head):
    if head == None:
        return None
    L, R, cur = None, None, head  # 左指针、有指针、游标
    while cur.next != None:
        L = R             # 左侧指针指向以前右侧指针位置
        R = cur           # 右侧指针前进一位指向当前游标位置
        cur = cur.next    # 游标每次向前进一位
        R.next = L        # 右侧指针指向左侧实现反转
    cur.next = R          # 当跳出 while 循环时 cur(原链表最后一个元素) R(原链表倒数第二个元素)
    return cur

if __name__ == '__main__':
    '''
    原始链表：1 -> 2 -> 3 -> 4
    反转链表：4 -> 3 -> 2 -> 1
    '''
    l1 = Node(1)
    l1.next = Node(2)
    l1.next.next = Node(3)
    l1.next.next.next = Node(4)
    l = list_reverse(l1)
    print l.val         # 4  反转后链表第一个值4
    print l.next.val    # 3  第二个值3

• 链表排序：归并排序算法实现

#! /usr/bin/env python
# -*- coding: utf-8 -*-
class ListNode(object):
    def __init__(self, val, next=None):
        self.val = val
        self.next = next

# 归并法: 对链表排序
class Solution:

    def sortList(self, head):
        if head is None or head.next is None:
            return head
        pre = head
        slow = head  # 使用快慢指针来确定中点
        fast = head
        while fast and fast.next:
            pre = slow
            slow = slow.next
            fast = fast.next.next

        left = head
        right = pre.next
        pre.next = None  # 从中间打断链表
        left = self.sortList(left)
        right = self.sortList(right)
        return self.merge(left, right)

    def merge(self, left, right):
        pre = ListNode(-1)
        first = pre
        while left and right:
            if left.val < right.val:
                pre.next = left
                pre = left
                left = left.next
            else:
                pre.next = right
                pre = right
                right = right.next
        if left:
            pre.next = left
        else:
            pre.next = right
        return first.next


node1 = ListNode(4)
node2 = ListNode(3)
node3 = ListNode(2)
node4 = ListNode(1)

node1.next = node2
node2.next = node3
node3.next = node4

s = Solution()
result = s.sortList(node1)

while (result != None):
    print result.val,    # 1 2 3 4
    result = result.next

• 对python列表排序：归并排序 对比

#!/usr/bin/env python
# -*- coding:utf-8 -*-
def mergesort(seq):
    if len(seq) <= 1:
        return seq
    mid = int(len(seq) / 2)
    left = mergesort(seq[:mid])
    right = mergesort(seq[mid:])
    return merge(left, right)

def merge(left, right):
    result = []
    i, j = 0, 0
    while i < len(left) and j < len(right):
        if left[i] <= right[j]:
            result.append(left[i])
            i += 1
        else:
            result.append(right[j])
            j += 1
    result += left[i:]
    result += right[j:]
    return result

if __name__ == '__main__':
    seq = [10,4,6,3,8,2,5,7]
    print mergesort(seq)  # [2, 3, 4, 5, 6, 7, 8, 10]

• 双链表
  • 双链表中每个节点有两个指针：一个指针指向后面节点、一个指向前面节点
    
• 双链表增删改查

#! /usr/bin/env python
# -*- coding: utf-8 -*-
class Node(object):
    """双向链表节点"""
    def __init__(self, item):
        self.item = item
        self.next = None
        self.prev = None


class DLinkList(object):
    """双向链表"""
    def __init__(self):
        self._head = None

    def is_empty(self):
        """判断链表是否为空"""
        return self._head == None

    def length(self):
        """返回链表的长度"""
        cur = self._head
        count = 0
        while cur != None:
            count += 1
            cur = cur.next
        return count

    def travel(self):
        """遍历链表"""
        cur = self._head
        while cur != None:
            print cur.item,
            cur = cur.next
        print ""

    def add(self, item):
        """头部插入元素"""
        node = Node(item)
        if self.is_empty():
            # 如果是空链表，将_head指向node
            self._head = node
        else:
            # 将node的next指向_head的头节点
            node.next = self._head
            # 将_head的头节点的prev指向node
            self._head.prev = node
            # 将_head 指向node
            self._head = node

    def append(self, item):
        """尾部插入元素"""
        node = Node(item)
        if self.is_empty():
            # 如果是空链表，将_head指向node
            self._head = node
        else:
            # 移动到链表尾部
            cur = self._head
            while cur.next != None:
                cur = cur.next
            # 将尾节点cur的next指向node
            cur.next = node
            # 将node的prev指向cur
            node.prev = cur

    def search(self, item):
        """查找元素是否存在"""
        cur = self._head
        while cur != None:
            if cur.item == item:
                return True
            cur = cur.next
        return False

    def insert(self, pos, item):
        """在指定位置添加节点"""
        if pos <= 0:
            self.add(item)
        elif pos > (self.length() - 1):
            self.append(item)
        else:
            node = Node(item)
            cur = self._head
            count = 0
            # 移动到指定位置的前一个位置
            while count < (pos - 1):
                count += 1
                cur = cur.next
            # 将node的prev指向cur
            node.prev = cur
            # 将node的next指向cur的下一个节点
            node.next = cur.next
            # 将cur的下一个节点的prev指向node
            cur.next.prev = node
            # 将cur的next指向node
            cur.next = node

    def remove(self, item):
        """删除元素"""
        if self.is_empty():
            return
        else:
            cur = self._head
            if cur.item == item:
                # 如果首节点的元素即是要删除的元素
                if cur.next == None:
                    # 如果链表只有这一个节点
                    self._head = None
                else:
                    # 将第二个节点的prev设置为None
                    cur.next.prev = None
                    # 将_head指向第二个节点
                    self._head = cur.next
                return
            while cur != None:
                if cur.item == item:
                    # 将cur的前一个节点的next指向cur的后一个节点
                    cur.prev.next = cur.next
                    # 将cur的后一个节点的prev指向cur的前一个节点
                    cur.next.prev = cur.prev
                    break
                cur = cur.next


if __name__ == "__main__":
    ll = DLinkList()
    ll.add(1)
    ll.add(2)
    # ll.append(3)
    # ll.insert(2, 4)
    # ll.insert(4, 5)
    # ll.insert(0, 6)
    # print "length:",ll.length()
    # ll.travel()
    # print ll.search(3)
    # print ll.search(4)
    # ll.remove(1)
    print "length:",ll.length()
    ll.travel()

• 双链表追加和遍历

#! /usr/bin/env python
# -*- coding: utf-8 -*-
class Node(object):
    def __init__(self, item):
        self.item = item
        self.next = None
        self.prev = None


class DLinkList(object):
    def __init__(self):
        self._head = None

    def is_empty(self):
        return self._head == None

    def append(self, item):
        node = Node(item)
        if self.is_empty():
            self._head = node
        else:
            cur = self._head
            while cur.next != None:
                cur = cur.next
            cur.next = node
            node.prev = cur

    def travel(self):
        cur = self._head
        while cur != None:
            print cur.item,
            cur = cur.next


if __name__ == '__main__':
    ll = DLinkList()
    ll.append(1)
    ll.append(2)
    ll.append(3)
    # print ll._head.item              # 打印第一个元素：1
    # print ll._head.next.item         # 打印第二个元素：2
    # print ll._head.next.next.item    # 打印第三个元素：3
    ll.travel()    # 1 2 3

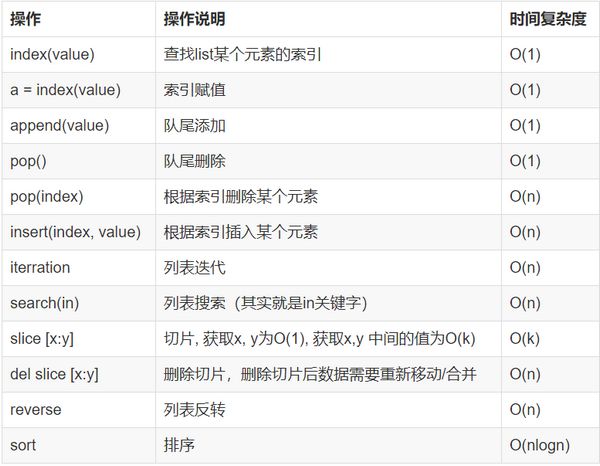
1.5 数组

• 数组定义

  • 所谓数组，就是相同数据类型的元素按一定顺序排列的集合

  • 在Java等其他语言中并不是所有的数据都能存储到数组中，只有相同类型的数据才可以一起存储到数组中。

  • 因为数组在存储数据时是按顺序存储的，存储数据的内存也是连续的，所以他的特点就是寻址读取数据比较容易，插入和删除比较困难。
    

• python中list与数组比较

  • python中的list是python的内置数据类型，list中的数据类不必相同的，而array的中的类型必须全部相同。
  • 在list中的数据类型保存的是数据的存放的地址，简单的说就是指针，并非数据
  • 否则这样保存一个list就太麻烦了，例如list1=[1,2,3,‘a’]需要4个指针和四个数据，增加了存储和消耗cpu。
    

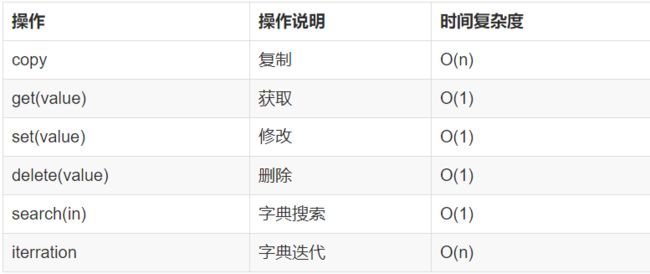
1.6 python中字典对象实现原理

注：字典类型是Python中最常用的数据类型之一，它是一个键值对的集合，字典通过键来索引，关联到相对的值，理论上它的查询复杂度是 O(1)

• 哈希表 (hash tables)

  • 哈希表（也叫散列表），根据关键值对(Key-value)而直接进行访问的数据结构。

  • 它通过把key和value映射到表中一个位置来访问记录，这种查询速度非常快，更新也快。

  • 而这个映射函数叫做哈希函数，存放值的数组叫做哈希表。

  • 通过把每个对象的关键字k作为自变量，通过一个哈希函数h(k)，将k映射到下标h(k)处，并将此对象存储在这个位置。

• 具体操作过程

  • 数据添加：把key通过哈希函数转换成一个整型数字，然后就将该数字对数组长度进行取余，取余结果就当作数组的下标，
    　　　　　　 将value存储在以该数字为下标的数组空间里。

  • 数据查询：再次使用哈希函数将key转换为对应的数组下标，并定位到数组的位置获取value。

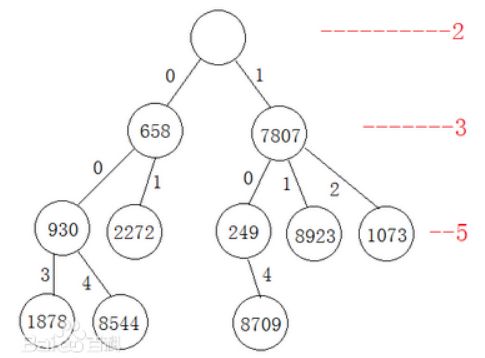
• **{“name”:”zhangsan”,”age”:26} 字典如何存储的呢? **

  • 比如字典{“name”:”zhangsan”,”age”:26}，那么他们的字典key为name、age，假如哈希函数h(“name”) = 1、h(“age”)=3,
  • 那么对应字典的key就会存储在列表对应下标的位置，[None, “zhangsan”, None, 26 ]

• 解决hash冲突
  

• python字典操作时间复杂度
  

1.7 树的概念

• 树的特性
  • 一棵树中的任意两个结点有且仅有唯一的一条路径连通；
  • 一棵树如果有n个结点，则它一定有n−1条边；
  • 在一棵树中加一条边将会构成一个回路。
• 二叉树

  • 二叉树是一种特殊的树，二叉树的特点是每个结点最多有两个儿子。

  • 二叉树使用范围最广，一颗多叉树也可以转化为二叉树。

• 满二叉树

  • 二叉树中每个内部节点都有两个儿子，满二叉树所有的叶节点都有相同的深度。

  • 满二叉树是一棵深度为h且有2h−1个结点的二叉树。

• 完全二叉树
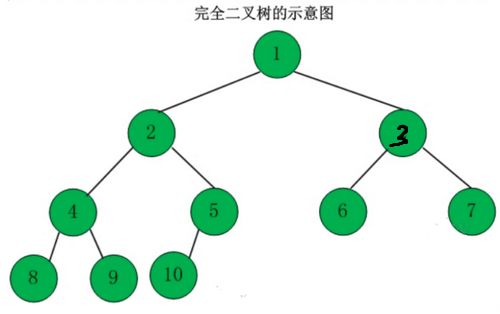
  • 若设二叉树的高度为h，除了第h层外，其他层的结点数都达到最大个数，第h层从右向左连续 缺若干个结点，则为完全二叉树。
    
• 树的特点

  • 如果一棵完全二叉树的父节点编号为K,则其左儿子的编号是2K,右儿子的结点编号为2K+1

  • 已知完全二叉树的总节点数为n求叶子节点个数：
    　　　　　　　　当n为奇数时：（n+1）/2
    　　　　　　　　当n为偶数时 : （n）/2

  • 已知完全二叉树的总节点数为n求父节点个数：为：n/2

  • 已知完全二叉树的总节点数为n求叶子节点为2的父节点个数：
    　　　　　　　　当n为奇数时：n/2
    　　　　　　　　当n为偶数时 : n/2-1

  • 如果一棵完全二叉树有N个结点，那么这棵二叉树的深度为【log2（N+1）log2（N+1）】（向上取整）

1.8 二叉树基本操作

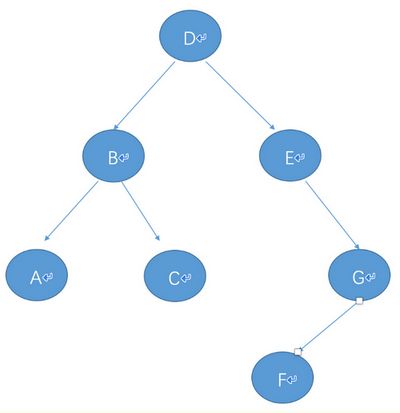
• 生成树结构
  • 前序遍历： DBACEGF（根节点排最先，然后同级先左后右）
  • 中序遍历： ABCDEFG (先左后根最后右）
  • 后序遍历： ACBFGED （先左后右最后根）
• 生成树形结构

#! /usr/bin/env python
# -*- coding: utf-8 -*-
class Node:
    def __init__(self,value=None,left=None,right=None):
        self.value=value
        self.left=left    #左子树
        self.right=right  #右子树

if __name__=='__main__':
    root=Node('D',Node('B',Node('A'),Node('C')),Node('E',right=Node('G',Node('F'))))

• 前序遍历

#! /usr/bin/env python
# -*- coding: utf-8 -*-
class Node:
    def __init__(self,value=None,left=None,right=None):
        self.value=value
        self.left=left    #左子树
        self.right=right  #右子树

def preTraverse(root):
     '''
     前序遍历
     '''
     if root==None:
         return
     print(root.value)
     preTraverse(root.left)
     preTraverse(root.right)

if __name__=='__main__':
    root=Node('D',Node('B',Node('A'),Node('C')),Node('E',right=Node('G',Node('F'))))
    print('前序遍历：')
    preTraverse(root)   #  DBACEGF

• 中序遍历

#! /usr/bin/env python
# -*- coding: utf-8 -*-
class Node:
    def __init__(self,value=None,left=None,right=None):
        self.value=value
        self.left=left    #左子树
        self.right=right  #右子树

def midTraverse(root):
    '''
    中序遍历
    '''
    if root == None:
        return
    midTraverse(root.left)
    print(root.value)
    midTraverse(root.right)

if __name__=='__main__':
    root=Node('D',Node('B',Node('A'),Node('C')),Node('E',right=Node('G',Node('F'))))
    print('中序遍历：')
    midTraverse(root)   #  ACBFGED

• 后序遍历

#! /usr/bin/env python
# -*- coding: utf-8 -*-
class Node:
    def __init__(self,value=None,left=None,right=None):
        self.value=value
        self.left=left    #左子树
        self.right=right  #右子树

def afterTraverse(root):
    '''
    后序遍历
    '''
    if root == None:
        return
    afterTraverse(root.left)
    afterTraverse(root.right)
    print(root.value)

if __name__=='__main__':
    root=Node('D',Node('B',Node('A'),Node('C')),Node('E',right=Node('G',Node('F'))))
    print('后序遍历：')
    afterTraverse(root)   #  ACBFGED

* 前序遍历步骤推演

前序排列原理：
#####此时执行preTraverse(root.left) 函数
'''
1、第一步 root=Node(D) print D，D入栈[D]
2、第二步 root=Node(D).left=Node(B) print B, B入栈[D,B]
3、第三步 root=Node(B).left=Node(A) print A, A入栈[D,B,A]
4、第四步 root=Node(A).left=None,没有进入递归，顺序执行preTraverse(root.right)
5、第五步 Node(A).right==None，也没有进入递归，此时preTraverse(A) 函数才会正真返回，A出栈[D,B]
6、第六步 A的上级调用函数为：preTraverse(B.left),所以接着会顺序执行preTraverse(B.right),B的左右节点访问后B出栈[D]
7、第七步 Node(B).right==Node(C) print C,C入栈[D,C]
8、第八步 Node(C).left==None, Node(C).right==None,访问完C的左右节点后函数返回C出栈，返回上级调用[D]
9、第九步 此时返回上级调用执行preTraverse(D.right)=Node(E) print E,D出栈，E入栈[E] 
'''

'''此时输出结果：DBACE'''

• 分层打印二叉树

#! /usr/bin/env python
# -*- coding: utf-8 -*-
class Node:
    def __init__(self,value=None,left=None,right=None):
        self.value=value
        self.left=left    #左子树
        self.right=right  #右子树

def layered_print( root):
    if not root:
        return []
    curLayer = [root]                           # 当前层的所有节点
    while curLayer:
        layerValue = []                         # 当前层的值
        nextLayer = []                          # 下一层的所有节点
        for node in curLayer:                   # 循环当前层所有节点并并获取所有value值
            layerValue.append(node.value)
            if node.left:
                nextLayer.append(node.left)        # 将当前层的左节点加入列表
            if node.right:
                nextLayer.append(node.right)        # 将当前层的右节点加入列表
                
        print layerValue                           # 打印当前层的值
        curLayer = nextLayer                      # 将循环下移一层


'''
['D']
['B', 'E']
['A', 'C', 'G']
['F']
'''

if __name__=='__main__':
    root=Node('D',Node('B',Node('A'),Node('C')),Node('E',right=Node('G',Node('F'))))
    layered_print(root)

1.9 hash树

• hash树描述（就是散列树）

  • 散列树选择从2开始的连续质数来建立一个十层的哈希树。

  • 第一层结点为根结点，根结点下有2个结点；

  • 第二层的每个结点下有3个结点；

  • 依此类推，即每层结点的子节点数目为连续的质数。

• hash树特点
  注：关系型数据库中，索引大多采用B/B+树来作为存储结构，而全文搜索引擎的索引则主要采用hash的存储结构，这两种数据结构有什么区别？

  • 如果是等值查询，那么哈希索引明显有绝对优势，因为只需要经过一次算法即可找到相应的键值；

  • 当然了，这个前提是，键值都是唯一的，如果键值不是唯一的，就需要先找到该键所在位置，然后再根据链表往后扫描，直到找到相应的数据；

  • 如果是范围查询检索，这时候哈希索引就毫无用武之地了，因为原先是有序的键值，经过哈希算法后，
    　　　　　　 有可能变成不连续的了，就没办法再利用索引完成范围查询检索；

  • 同理，哈希索引也没办法利用索引完成排序，以及like ‘xxx%’ 这样的部分模糊查询（这种部分模糊查询，其实本质上也是范围查询）；

• 建立hash树

  • 选择从2开始的连续质数来建立一个十层的哈希树。

  • 第一层结点为根结点，根结点下有2个结点；第二层的每个结点下有3个结点；

  • 依此类推，即每层结点的子节点数目为连续的质数。到第十层，每个结点下有29个结点。

  • 同一结点中的子结点，从左到右代表不同的余数结果。
    　　　　　　　　例如：第二层结点下有三个子节点。那么从左到右分别代表：除3余0，除3余1，除3余2.对质数进行取余操作得到的余数决定了处理的路径。

  • 以随机的10个数的插入为例，来图解HashTree的插入过程。
    

  • 其实也可以把所有的键-值节点放在哈希树的第10层叶节点处，这第10层的满节点数就包含了所有的整数个数，
    　　　　 　　 但是如果这样处理的话，所有的非叶子节点作为键-值节点的索引，这样使树结构庞大，浪费空间。

• 查找编辑

  • 哈希树的节点查找过程和节点插入过程类似，就是对关键字用质数序列取余，根据余数确定下一节点的分叉路径，直到找到目标节点。
  • 如上图，最小”哈希树(HashTree)在从4G个对象中找出所匹配的对象，比较次数不超过10次，也就是说：最多属于O(10)。
  • 在实际应用中，调整了质数的范围，使得比较次数一般不超过5次。
  • 也就是说：最多属于O(5)，因此可以根据自身需要在时间和空间上寻求一个平衡点。

• 删除编辑

  • 哈希树的节点删除过程也很简单，哈希树在删除的时候，并不做任何结构调整。

  • 只是先查到到要删除的节点，然后把此节点的“占位标记”置为false即可（即表示此节点为空节点，但并不进行物理删除）。

• hash树优点

  • 结构简单
    • 从哈希树的结构来说，非常的简单，每层节点的子节点个数为连续的质数。
    • 子节点可以随时创建，因此哈希树的结构是动态的，也不像某些哈希算法那样需要长时间的初始化过程。
    • 哈希树也没有必要为不存在的关键字提前分配空间。
  • 查找迅速
    • 从算法过程我们可以看出，对于整数，哈希树层级最多能增加到10
    • 因此最多只需要十次取余和比较操作，就可以知道这个对象是否存在，这个在算法逻辑上决定了哈希树的优越性。
  • 结构不变

    • 从删除算法中可以看出，哈希树在删除的时候，并不做任何结构调整。

    • 常规树结构在增加元素和删除元素的时候都要做一定的结构调整，否则他们将可能退化为链表结构，而导致查找效率的降低。

    • 哈希树采取的是一种“见缝插针”的算法，从来不用担心退化的问题，也不必为优化结构而采取额外的操作，因此大大节约了操作时间。

• 缺点编辑

  • 哈希树不支持排序，没有顺序特性。

  • 如果在此基础上不做任何改进的话并试图通过遍历来实现排序，那么操作效率将远远低于其他类型的数据结构。

• hash索引使用范围
  总结：哈希适用在小范围的精确查找，在列数据很大，又不需要排序，不需要模糊查询，范围查询时有用

  • hash索引仅满足“=”、“IN”和“<=>”查询，不能使用范围查询
    因为hash索引比较的是经常hash运算之后的hash值，因此只能进行等值的过滤，不能基于范围的查找，
    因为经过hash算法处理后的hash值的大小关系，并不能保证与处理前的hash大小关系对应。

  • hash索引无法被用来进行数据的排序操作
    由于hash索引中存放的都是经过hash计算之后的值，而hash值的大小关系不一定与hash计算之前的值一样，
    所以数据库无法利用hash索引中的值进行排序操作。

  • 对于组合索引，Hash 索引在计算 Hash 值的时候是组合索引键合并后再一起计算 Hash 值，
    而不是单独计算 Hash 值，所以通过组合索引的前面一个或几个索引键进行查询的时候，Hash 索引也无法被利用。

  • Hash 索引遇到大量Hash值相等的情况后性能并不一定就会比B-Tree索引高。
    对于选择性比较低的索引键，如果创建 Hash 索引，那么将会存在大量记录指针信息存于同一个 Hash 值相关联。
    这样要定位某一条记录时就会非常麻烦，会浪费多次表数据的访问，而造成整体性能低下。

2.0 B-tree 和 B+tree

相关博客：https://blog.csdn.net/Hanmin_hm/article/details/104572959