【算法】麦克风阵列的自适应降噪算法
参考链接:
语音自适应滤波器的设计
说说鸡尾酒会问题和程序实现
【PUDN】自适应变步长的龙格库塔法
参考文献:
[1]黄颖. 基于麦克风阵列手机消噪方案的应用与实现[D].上海交通大学,2012.
[2]王超. 频域卷积混合盲分离研究[D].上海大学,2008.
【论文】自适应谱线增强器在生物雷达中的应用
一、理论基础
在实际应用中,常常无法的带信号和噪声统计特性的鲜艳信息,在此情况下自适应滤波技术能够获得极佳的滤波性能,因此具有很好的应用价值,常用的自适应滤波器技术有:最小均方(LMS)自适应滤波器,递推最小二乘(RLS)滤波器,格型滤波器和无限冲激响应(IIR)滤波器,。这些自适应滤波技术的应用又包括:自适应噪声抵消,自适应谱线增强和陷波。
LMS自适应滤波器事使滤波器的输出信号于期望响应之间的误差的均方值为最小,因此称为最小均方(LMS)自适应滤波器。
1、基于LMS算法
构成自适应数字滤波器的基本部件是自适应线性组合器,设线性组合的M个输入为x(k-1)…,x(k-M),其输出有y(k)是这些输入加权后的线性组合,即
∑ i = 0 M W i x ( k − i ) \sum_{i=0}^{M}{W_{i}x(k-i)} i=0∑MWix(k−i)
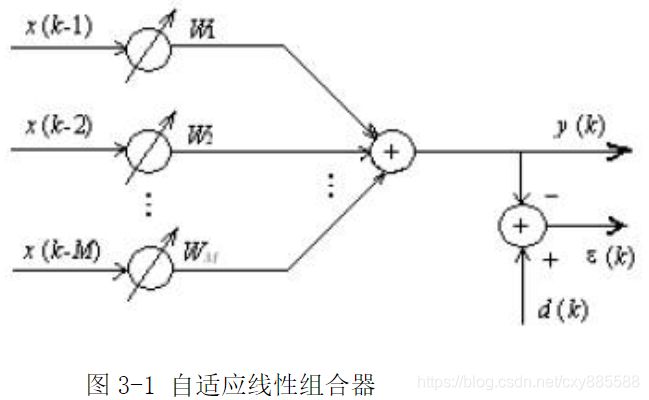 定义权向量, W = [ W 1 , W 2 , W 3 , . . . , W m ] W=[W_{1},W_{2},W_{3},...,W_{m}] W=[W1,W2,W3,...,Wm] X ( k ) = [ x ( k − 1 ) . . . , x ( k − M ) ] T X(k)=[x(k-1)...,x(k-M)]_{}^{T} X(k)=[x(k−1)...,x(k−M)]T令d(k)代表“所期望的响应”,并定义误差信号 ε ( k ) = d ( k ) − y ( k ) = d ( k ) − ∑ i = 0 M W i x ( k − i ) \varepsilon(k)=d(k)-y(k)=d(k)-\sum_{i=0}^{M}{W_{i}x(k-i)} ε(k)=d(k)−y(k)=d(k)−i=0∑MWix(k−i)写成向量形式为: ε ( k ) = d ( k ) − W T X ( k ) = d ( k ) − X T W ( k ) \varepsilon(k)=d(k)-W_{}^{T}X(k)=d(k)-X_{}^{T}W(k) ε(k)=d(k)−WTX(k)=d(k)−XTW(k)误差平方为: ε 2 ( k ) = d 2 ( k ) − 2 d ( k ) X T ( k ) W + W T X ( k ) X T ( k ) W \varepsilon^2(k)=d^2(k)-2d(k)X^T(k)W+W^TX(k)X^T(k)W ε2(k)=d2(k)−2d(k)XT(k)W+WTX(k)XT(k)W上式两边取数学期望为,得均方误差为
定义权向量, W = [ W 1 , W 2 , W 3 , . . . , W m ] W=[W_{1},W_{2},W_{3},...,W_{m}] W=[W1,W2,W3,...,Wm] X ( k ) = [ x ( k − 1 ) . . . , x ( k − M ) ] T X(k)=[x(k-1)...,x(k-M)]_{}^{T} X(k)=[x(k−1)...,x(k−M)]T令d(k)代表“所期望的响应”,并定义误差信号 ε ( k ) = d ( k ) − y ( k ) = d ( k ) − ∑ i = 0 M W i x ( k − i ) \varepsilon(k)=d(k)-y(k)=d(k)-\sum_{i=0}^{M}{W_{i}x(k-i)} ε(k)=d(k)−y(k)=d(k)−i=0∑MWix(k−i)写成向量形式为: ε ( k ) = d ( k ) − W T X ( k ) = d ( k ) − X T W ( k ) \varepsilon(k)=d(k)-W_{}^{T}X(k)=d(k)-X_{}^{T}W(k) ε(k)=d(k)−WTX(k)=d(k)−XTW(k)误差平方为: ε 2 ( k ) = d 2 ( k ) − 2 d ( k ) X T ( k ) W + W T X ( k ) X T ( k ) W \varepsilon^2(k)=d^2(k)-2d(k)X^T(k)W+W^TX(k)X^T(k)W ε2(k)=d2(k)−2d(k)XT(k)W+WTX(k)XT(k)W上式两边取数学期望为,得均方误差为
E ( ε 2 ( k ) ) = E ( d 2 ( k ) ) − 2 E ( d ( k ) X T ( k ) W ) + W T E ( X ( k ) X T ( k ) ) W E(\varepsilon^2(k))=E(d^2(k))-2E(d(k)X^T(k)W)+W^TE(X(k)X^T(k))W E(ε2(k))=E(d2(k))−2E(d(k)XT(k)W)+WTE(X(k)XT(k))W定义互相关函数行向量 R x d T R_{xd}^{T} RxdT:
R x d T = E ( d ( k ) X T ( k ) ) — — ( 1 − 9 ) R_{xd}^{T}=E(d(k)X^T(k))——(1-9) RxdT=E(d(k)XT(k))——(1−9)和自相关函数矩阵
R X X = E ( X ( k ) X T ( k ) ) — — ( 1 − 10 ) R_{XX}=E(X(k)X^T(k))——(1-10) RXX=E(X(k)XT(k))——(1−10)则均方误差可更改表述为
E ( ε 2 ( k ) ) = E ( d 2 ( k ) ) − 2 R x d T W + W T R X X W — — ( 1 − 11 ) E(\varepsilon^2(k))=E(d^2(k))-2R_{xd}^{T}W+W^TR_{XX}W——(1-11) E(ε2(k))=E(d2(k))−2RxdTW+WTRXXW——(1−11)
利用式1-10求最佳权系数向量得精确解需要知道 R X X R_{XX} RXX和 R x d R_{xd} Rxd的先验统计知识,而且还需要进行矩阵求逆等运算。这种算法的根据是最优化方法中的最速下降法。根据最速下降法,“下一时刻”权系数向量W(k+1)应该等于“现时刻”权系数向量W(k)加上一个负均方误差梯度 − ▽ ( k ) -\triangledown(k) −▽(k)的比例项,即 W ( k + 1 ) = W ( k ) − μ ▽ ( k ) W(k+1)=W(k)-\mu\triangledown(k) W(k+1)=W(k)−μ▽(k)式中, μ \mu μ是一个控制收敛速度于稳定性的常数,称之为收敛因子。
不难看出,LMS算法有两个关键,梯度 ▽ ( k ) \triangledown(k) ▽(k)的计算以及收敛因子 μ \mu μ的选择。
1.1 ▽ ( k ) \triangledown(k) ▽(k)的近似计算
精确计算梯度 ▽ ( k ) \triangledown(k) ▽(k)是十分苦难的,一种粗略的但是却十分有效的计算 ▽ ( k ) \triangledown(k) ▽(k)的近似方法是:直接取 ε 2 ( k ) \varepsilon^2(k) ε2(k)作为均方误差 E ( ε 2 ( k ) ) E(\varepsilon^2(k)) E(ε2(k))的估计值,即
▽ ^ ( k ) = ▽ [ ε 2 ( k ) ] = 2 ε ( k ) ▽ ( k ) \hat{\triangledown}(k)=\triangledown[\varepsilon^2(k)]=2\varepsilon(k)\triangledown(k) ▽^(k)=▽[ε2(k)]=2ε(k)▽(k)得到梯度估计值
▽ ^ ( k ) = − 2 ε ( k ) X ( k ) \hat{\triangledown}(k)=-2\varepsilon(k)X(k) ▽^(k)=−2ε(k)X(k)于是,Widrow-Hoff LMS算法最终为
W ( k + 1 ) = W ( k ) + 2 μ ε ( k ) X ( k ) — — ( 1 − 14 ) W(k+1)=W(k)+2\mu\varepsilon(k)X(k)——(1-14) W(k+1)=W(k)+2με(k)X(k)——(1−14)式子1-14的实现方框图如下图所示

下面分析梯度估计值 ▽ ^ ( k ) \hat{\triangledown}(k) ▽^(k)的无偏性。 ▽ ^ ( k ) \hat{\triangledown}(k) ▽^(k)的数学期望为
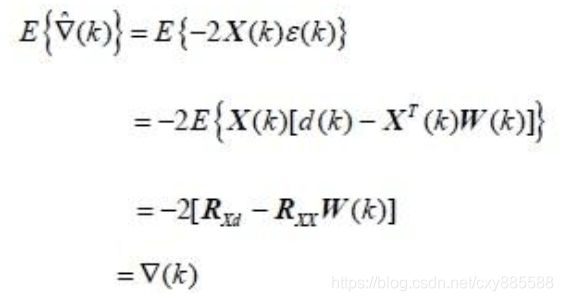 ——(1-15)
——(1-15)
在上面的推导过程中,利用了d(k)和 ε ( k ) \varepsilon(k) ε(k)二者皆为标量的事实。在得到最后的结果时,利用了式子1-9和1-15表明,梯度估值 ▽ ^ ( k ) \hat{\triangledown}(k) ▽^(k)是无偏估计。
1.2 μ \mu μ的选择
对权系数向量更新公式1-14两边取数学期望,得
E ( W ( k + 1 ) ) = E ( W ( l k ) ) + 2 μ E ( ε ( k ) X ( k ) ) = ( I − 2 μ R X X ) E ( W ( k ) ) + 2 μ R x d E(W(k+1))=E(W(lk))+2\mu E(\varepsilon(k)X(k))=(I-2\mu R_{XX})E(W(k))+2\mu R_{xd} E(W(k+1))=E(W(lk))+2μE(ε(k)X(k))=(I−2μRXX)E(W(k))+2μRxd
式子中,I为单位矩阵, R x d = E ( d ( k ) X ( k ) ) R_{xd}=E(d(k)X(k)) Rxd=E(d(k)X(k))和 R X X = E ( X ( k ) X T ( k ) ) R_{XX}=E(X(k)X^T(k)) RXX=E(X(k)XT(k))。
当时, k = 0 k=0 k=0时
E ( W ( 1 ) ) = ( I − 2 μ R X X ) E ( W ( 0 ) ) + 2 μ R x d E(W(1))=(I-2\mu R_{XX})E(W(0))+2\mu R_{xd} E(W(1))=(I−2μRXX)E(W(0))+2μRxd
当时, k = 1 k=1 k=1时,利用上式结果,则有
E ( W ( 2 ) ) = ( I − 2 μ R X X ) E ( W ( 1 ) ) + 2 μ R x d ( I − 2 μ R X X ) E ( W ( 0 ) ) + 2 μ ∑ i = 0 1 ( I − 2 μ R X X ) i R x d E(W(2))=(I-2\mu R_{XX})E(W(1))+2\mu R_{xd}(I-2\mu R_{XX})E(W(0))+2\mu\sum_{i=0}^{1}(I-2\mu R_{XX})^iR_{xd} E(W(2))=(I−2μRXX)E(W(1))+2μRxd(I−2μRXX)E(W(0))+2μi=0∑1(I−2μRXX)iRxd
起始时, E ( W ( 0 ) ) = W ( 0 ) E(W(0))=W(0) E(W(0))=W(0)
故重复以上迭代至k+1,则有
E ( W ( k + 1 ) ) = ( I − 2 μ R X X ) k + 1 W ( 0 ) + 2 μ ∑ i = 0 1 ( I − 2 μ R X X ) i R x d — — ( 1 − 18 ) E(W(k+1))=(I-2\mu R_{XX})^{k+1}W(0)+2\mu\sum_{i=0}^{1}(I-2\mu R_{XX})^iR_{xd}——(1-18) E(W(k+1))=(I−2μRXX)k+1W(0)+2μi=0∑1(I−2μRXX)iRxd——(1−18)由于 R X X R_{XX} RXX是实值得对称阵,我们可以写出其特征值分解式
R X X = Q ∑ Q T = Q ∑ Q − 1 — — ( 1 − 19 ) R_{XX}=Q\sum{Q^T}=Q\sum{Q^{-1}}——(1-19) RXX=Q∑QT=Q∑Q−1——(1−19)这里,我们利用 了正定阵Q的性质 Q T = Q − 1 Q^T=Q^{-1} QT=Q−1,且 ∑ = d i a g ( λ 1 , . . . λ M ) \sum=diag(\lambda_{1},...\lambda_{M}) ∑=diag(λ1,...λM)是对角阵,其对角元素 λ i \lambda_{i} λi是 R X X R_{XX} RXX的特征值。将式1-18带入式1-19后得
E ( W ( k + 1 ) ) = ( I − 2 μ Q ∑ Q − 1 ) k + 1 W + 2 μ ∑ i = 0 k ( I − 2 μ Q ∑ Q − 1 ) i R x d — — ( 1 − 20 ) E(W(k+1))=(I-2\mu Q\sum{Q^{-1}})^{k+1}W+2\mu\sum_{i=0}^{k}(I-2\mu Q\sum{Q^{-1}})^iR_{xd}——(1-20) E(W(k+1))=(I−2μQ∑Q−1)k+1W+2μi=0∑k(I−2μQ∑Q−1)iRxd——(1−20)
E ( W ( k + 1 ) ) = Q ∑ − 1 Q − 1 R x d = R X X − 1 R x d = W o p t — — ( 1 − 20 ) E(W(k+1))=Q\sum^{-1}Q^{-1}R_{xd}=R_{XX}^{-1}R_{xd}=W_{opt}——(1-20) E(W(k+1))=Q∑−1Q−1Rxd=RXX−1Rxd=Wopt——(1−20)由此可见,当迭代次数无限增加时,权系数向量得数学期望可收敛至wiener解,其条件是对角阵 ( I − 2 μ ∑ ) (I-2\mu\sum) (I−2μ∑)的所有对角元素均小于1,即 0 < μ < 1 λ m a x 0<\mu<\frac{1}{\lambda_{max}} 0<μ<λmax1
其中, λ m a x \lambda_{max} λmax是 R X X R_{XX} RXX的最大特征值。 μ \mu μ称为收敛因子,它决定达到式1-20的速率。事实上, W ( k ) W(k) W(k)收敛于 W o p t W_{opt} Wopt由比值 d = λ m a x / λ m i n d=\lambda_{max}/\lambda_{min} d=λmax/λmin决定,该比值叫做谱动态范围。大的 d d d值预示要花很长的时间才会收敛到最佳权值。克服这一困难的方法之一是产生正交数据。
验证函数直接使用LMS实现成matlab中的一个函数,在测试LMS算法中调用LMS函数即可实现以下图形。

function [yn,W,en] = LMS(xn,dn,M,mu,itr)
%LMS(least mean squre)最小均方差算法
%%%%%%%%%%%%%输入参数:%%%%%%%%%%%%%%%%%%%
%xn 输入信号的序列(列向量)
%dn 所期望的响应序列(列向量)
%M 滤波器的阶数(标量)
%mu 收敛因子(步长)(标量)要求大于0,小于xn的相关矩阵最大特征值的倒数1/lamuda[max]
%itr 迭代次数(标量)默认为xnde changdu ,M<itr<length(xn)
%%%%%%%%%%%%%%输出参数:%%%%%%%%%%%%%%%%%
%W 滤波器的权值矩阵(矩阵)大小为M*itr
%en 误差序列(itr*1)(列向量)
%yn 实际输出序列(列向量)
%%%%%%%%%%%%%%%参数个数必须时4个或者5个%%%%%%%%%%%%%
if nargin == 4
itr = length(xn);
elseif nargin = 5
if itr>length(xn) | itr<M
error('迭代次数过大或过小');
end
else
error('请检查输入参数的个数');
end
%%%%%%%%%%%%初始化参数%%%%%%%%%%%%
en = zero(itr,1);
W = zeros(M,itr);
%%%%%%%%%%%%迭代计算%%%%%%%%%%%%
for k = M:itr %第k次迭代
x = xn(k:-1:k-M-+1); %滤波器M个抽头的输入
y = W(:,k-1).'* x; %滤波器的输出
en(k) = dn(k) - y; %第k次迭代的误差
%%%%%滤波器权值计算的迭代值%%%%%
W(:,k) = W(:,k-1) + 2*mu*en(k)*x;
end
%%%%%%%%%%%%求最优时滤波器的输出序列%%%%%%%%%%
yn = inf *ones(size(xn));
for k = M:length(xn)
x = xn(k:-1:k-M+1);
yn(k) = W(:,end).'* x;
end
LMS算法测试
%%%%%%%%%%%%%验证所设计的自适应滤波器%%%%%%%%%%%
%%%%%function main()
close all;
%%%调用周期信号%%%%%
t = 0:99;
xs = 10*sin(0.5*t);
figure(1);
subplot(2,1,1);
plot(t,xs);grid;
ylabel('幅值');
title('it{输入周期性信号}');
%%%%%噪声产生%%%%%
randn('state',sum(100*clock));
xn = randn(1,100);
subplot(2,1,2);
plot(t,xn);grid;
ylabel('幅值');
xlabel('时间');
title('it{随机噪声信号}');
%%%%%信号滤波%%%%%
xn = xs + xn;
xn = xn.'; %输入信号序列
dn = xs.';
M = 20';
lambda_max = max(eig(xn*xn.'));
mu = rand()*(1/lambda_max);
[yn,W,en] = LMS(xn,dn,M,mu);
%%%%绘制滤波器输入信号%%%%%%
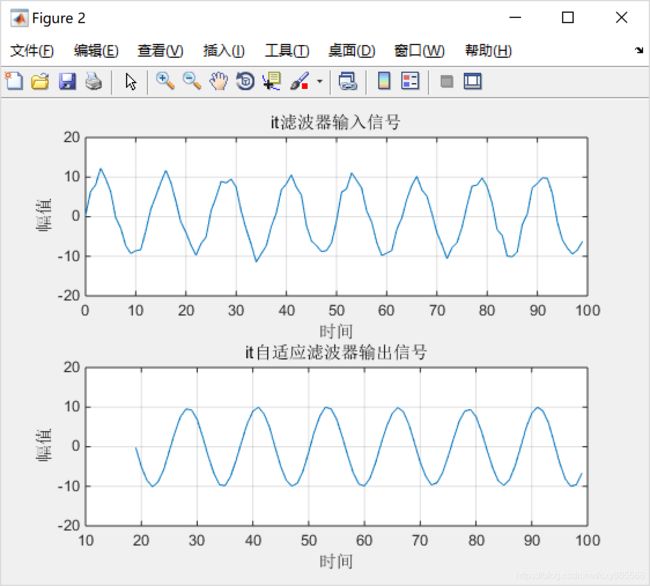
figure(2);
subplot(2,1,1);
plot(t,xn);grid;
ylabel('幅值');
xlabel('时间');
title('it{滤波器输入信号}');
%%%%绘制滤波器输出信号%%%%%%
subplot(2,1,2);
plot(t,yn);grid;
ylabel('幅值');
xlabel('时间');
title('it{自适应滤波器输出信号}');
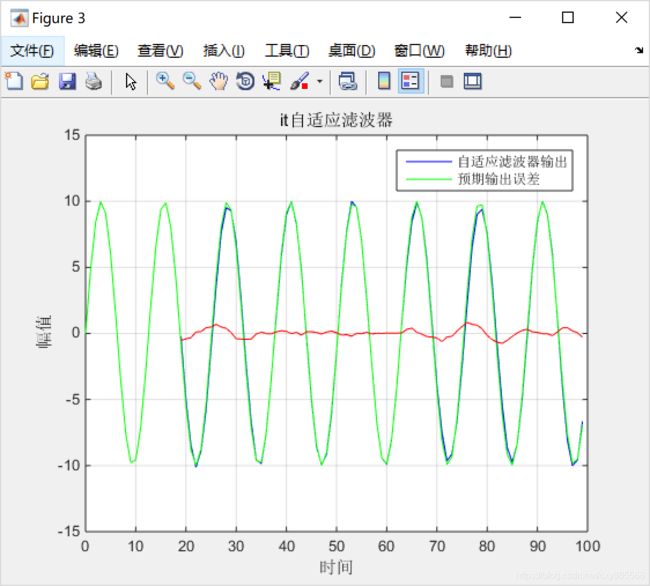
%%%绘制自适应滤波器输出信号,预期输出信号和两者的误差%%%%%
figure(3);
plot(t,yn,'b',t,dn,'g',t,dn-yn,'r');grid;
legend('自适应滤波器输出','预期输出误差');
ylabel('幅值');
xlabel('时间');
title('it{自适应滤波器}');
RLS算法matlab实现:
[primary,Fs,Nbits] = wavread('RLSprimsp.wav');
x = primary'; %含噪声的信号
ref = wavread('RLSrefns.wav');
r = ref'; % 输入噪声序列
M = 32 ; %设置序列长度
L = length (x); %数据的长度
Lambda = 0.999; %遗忘因子
Delta = 0.001 ; %初始化因子
ab = rand(M,1); % 产生均匀分布的随机数矩阵
%RLS算法
y = filter (ab,1,x);
E = eye (M,M); %生成单位矩阵
IR = Delta * E ;
wn = zeros (M,1) ; %把权值初始化
for n = M : L
xn = x(n); %当前x(n)
rn = r(n:-1:n-M+1) ; %当前r(n)
en = xn - rn*wn;
g = rn*IR;
IR = 1/Lambda*[IR - (IR*rn'*rn*IR)/(Lambda+rn*IR*rn')];
wn = wn + g' .* en;
v = rn * wn;
e(n) = xn - v;
end
for n = M : L
xn = x(n); %当前x(n)
rn = r(n:-1:n-M+1) ; %当前r(n)
v = rn * wn;
e(n) = xn - v;
end
figure(1) %建立图形窗口
subplot(2,1,1);
plot(x); %建立线性图形
subplot(2,1,2);
plot(r);
figure(2)
subplot(3,1,1);
plot(e);
subplot(3,1,2);
spy1=2*abs(fft(x))/L;
spy1=spy1(1:L/2);
df=Fs/L;
f=(0:L/2-1)*df;
plot (f,spy1);
subplot(3,1,3);
N = length(e);
spy2=2*abs(fft(e))/N;
spy2=spy2(1:N/2);
df=Fs/N;
f=(0:N/2-1)*df;
figure(3);
plot (f,spy2);
xlabel ('f(Hz)');
ylabel('原始语音的幅度谱');
audiowrite('eaudio.wav',e,Fs);