高通滤波法、微分算子法、神经网络方法实现图像边缘检测

边缘检测（Edge detection）是图像处理和计算机视觉中的基本问题，边缘检测的目的是标识数字图像中亮度变化明显的点。本文使用多种不同的方法，实现对 Lena 肖像的边缘检测，研究分析各算法的效果和优缺点。所涉及的方法如下：

• 高通滤波法

  • 理想高通滤波器
  • Butterworth 高通滤波器
  • 指数高通滤波器

• 微分算子法

  • Roberts 算子
  • Sobel 算子
  • Laplacian 算子
  • Canny 算子

• 神经网络方法

  • HED 算法

高通滤波法

图像中的边缘或线条等细节部分与图像频谱的高频分量相对应，因此采用高通滤波让高频分量顺利通过，使图像的边缘或线条细节变得清楚，实现边缘提取和图像锐化。

常见的高通滤波器包括：理想高通滤波器、Butterworth 高通滤波器、指数高通滤波器等。

理想高通滤波器

理想高通滤波器的传递函数 $H(u,v)$ 满足下式：
$$H(u,v)=\{\begin{array}{ll}1,& D(u,v)>D_0\\ 0,& D(u,v)\le D_0\end{array}$$
理想高通滤波器只是一种理想状况下的滤波器，不能用实际的电子器件实现。

Butterworth 高通滤波器

Butterworth 高通滤波器的传递函数 $H(u,v)$ 如下：
$$H(u,v)=\frac{1}{1+[D_0/D(u,v){]}^{2n}}$$
式中，$n$ 为阶数，$D_0$ 为截止频率。

Butterworth 高通滤波器在高低频率间的过渡比较平滑，所以由其得到的输出图像的振铃现象不明显。

指数高通滤波器

指数高通滤波器的传递函数 $H(u,v)$ 如下：
$$H(u,v)=\exp \{-[\frac{D_0}{D(u,v)}{]}^n\}$$
式中，变量 $n$ 控制从原点算起的传递函数 $H(u,v)$ 的增长率。

指数高通滤波器的另一种常用的传递函数如下式所示：
$$H(u,v)=\exp \{[\ln (\frac{1}{\sqrt{2}})][\frac{D_0}{D(u,v)}{]}^n\}$$

代码实现

为了在频率域中实现高通滤波，先通过傅里叶变换得到图像的频谱，根据不同滤波器的不同传递函数，对频率进行相应的过滤，最后再对其进行傅里叶反变换，得到滤波后的图像。

傅里叶变换

img = plt.imread('images/lena.bmp')
fft_shift = np.fft.fftshift(np.fft.fft2(img))	# 变换后将零频分量移到频谱中心
fft_img = np.log(np.abs(fft_shift))				# 可视化

实现三种滤波器

def distance(shape):		# 计算每个像素到中心原点的距离
    n, m = shape
    u = np.arange(n)
    v = np.arange(m)
    u, v = np.meshgrid(u, v)
    return np.sqrt((u - n//2)**2 + (v - m//2)**2)
    
def ideal_filter(shape, d0):
    d = distance(shape)
    mask = d > d0
    return mask.astype(int)

def butterworth_filter(shape, d0, order=1):
    d = distance(shape)
    mask = 1 / (1 + (d0 / d)**(2 * order))
    return mask

def exponential_filter(shape, d0, order=1):
    d = distance(shape)
    mask = np.exp(-(d0 / d)**order)
    return mask

滤波后进行傅里叶反变换

ifft_shift = np.fft.ifftshift(fft_shift * mask)
ifft_img = np.abs(np.fft.ifft2(ifft_shift))

运行结果及分析

下图中，从上到下依次展示了使用理想高通滤波器、Butterworth 高通滤波器和指数高通滤波器对 Lena 进行边缘检测，在不同的截止频率 $D_0$ 下（10、20、40、80）所得到的频谱图以及滤波后的图像输出。

通过对比可以发现，使用理想高通滤波器得到的结果有明显的振铃现象，而 Butterworth 高通滤波器和指数高通滤波器的结果相近，均具有较好的效果。从频谱图中也可以看出，理想高通滤波器对频率的截断非常陡峭，在临界点发生了突变，而后两者的滤波比较平滑，是一种在高低频率间逐渐过渡的过程。

微分算子法

针对由于平均或积分运算而引起的图像模糊，可用微分运算来实现图像的锐化。微分运算是求信号的变化率，有加强高频分量的作用，从而使图像轮廓清晰。

常见的边缘检测算子包括：Roberts 算子、Sobel 算子、Laplacian 算子、Canny 算子等。各种算子的存在就是对这种导数分割原理进行的实例化计算，是为了在计算过程中直接使用的一种计算单位。实际使用时，通常用各种算子对应的模板对原图进行卷积运算，从而提取出图像的边缘信息。

上述各算子的具体定义就不展开赘述了，具体可以参考相关书籍或文章。这里通过一张表对这些算子进行简要的介绍和比较。

算子	介绍及优缺点比较
Roberts	一种最简单的算子，采用对角线方向相邻两像素之差近似梯度幅值检测边缘。检测垂直边缘的效果好于斜向边缘，定位精度高，但是对噪声敏感，对具有陡峭边缘且含噪声少的图像效果较好。
Sobel	根据像素点上下左右四邻域灰度加权差检测边缘，类似局部平均运算，因此对噪声具有平滑作用，对灰度渐变和噪声较多的图像处理效果比较好，对边缘定位比较准确。
Laplacian	属于二阶微分算子，在只考虑边缘点的位置而不考虑周围的灰度差时适合用该算子进行检测。对噪声非常敏感，只适用于无噪声图像。存在噪声的情况下，使用该算子检测边缘之前需要先进行低通滤波，因此通常把 Laplacian 算子和平滑算子结合起来生成一个新的模板。
Canny	该算子功能比前面几种都要好，不容易受噪声的干扰，能够检测到真正的弱边缘，但是实现起来较为麻烦，是一个具有滤波、增强、检测的多阶段的优化算子。在进行处理前，Canny 算子先利用高斯平滑滤波器来平滑图像以除去噪声。Canny 分割算法采用一阶偏导的有限差分来计算梯度幅值和方向，在处理过程中，该算子还将经过一个非极大值抑制的过程，最后采用两个阈值来连接边缘。

代码实现

Roberts、Sobel 以及 Laplacian 算子方法均为手工实现：先根据不同算子对应的模板，分别定义对单个像素块的卷积运算函数，然后在图像上滑动模板，调用该函数计算每一个卷积块，最终得到经过各算子微分后的输出图像。对于 Canny 算子，由于其实现过程比较复杂，这里选择直接调用 OpenCV 中的 Canny() 函数。

实现前三种算子

def roberts_operator(block):
    kernel1 = np.array([[1,0], [0,-1]])
    kernel2 = np.array([[0,-1], [1,0]])
    return np.abs(np.sum(block[1:,1:] * kernel1)) + np.abs(np.sum(block[1:,1:] * kernel2))

def sobel_operator(block, orientation):		# 水平和垂直两个方向
    if orientation == 'horizontal':
        kernel = np.array([[-1,-2,-1], [0,0,0], [1,2,1]])
    elif orientation == 'vertical':
        kernel = np.array([[-1,0,1], [-2,0,2], [-1,0,1]])
    else:
        raise('Orientation Error')
    return np.abs(np.sum(block * kernel))

def laplacian_operator(block):
    kernel = np.array([[0,-1,0], [-1,4,-1], [0,-1,0]])
    return np.abs(np.sum(block * kernel))

滑动计算卷积块

def operator_process(img, operator_type, orientation=None):
    n, m = img.shape
    res = np.zeros((n, m))
    for i in range(1, n-1):
        for j in range(1, m-1):
            if operator_type == 'roberts':
                res[i][j] = roberts_operator(img[i-1:i+2, j-1:j+2])
            elif operator_type == 'sobel':
                res[i][j] = sobel_operator(img[i-1:i+2, j-1:j+2], orientation)
            elif operator_type == 'laplacian':
                res[i][j] = laplacian_operator(img[i-1:i+2, j-1:j+2])
            else:
                raise('Operator Type Error')
    return res

调用 OpenCV 中的 Canny 算子

canny_res = cv2.Canny(img, threshold1, threshold2)		# 设置高低阈值参数

运行结果及分析

使用 Roberts 算子、Laplacian 算子以及水平和垂直两个方向的 Sobel 算子进行边缘检测所得到的结果如下图所示：

可以看到，Roberts 算子简单但有效，已经能实现比较好的边缘检测效果；而 Laplacian 算子的效果相对较差，边缘不是很清晰，还出现了很多噪点；Sobel 算子整体表现也较好，可以明显地看出水平和垂直两个方向上结果的差别，前者对水平边缘响应最大（如眼眶、嘴唇、下巴处），后者对垂直边缘响应最大（如鼻梁、两侧脸颊处）。

下图显示了使用 OpenCV 自带的 Canny 算子在不同阈值下的输出结果，其中低阈值 threshold1 依次取 30、50、80、120、150，而高阈值 threshold2 根据 Canny 算法的推荐，均取为 threshold1 的 3 倍。

低于 threshold1 的像素被认为不是边缘，高于 threshold2 的像素被认为是边缘，介于二者之间的则会根据相邻的像素点进一步确定。从图中也可以看出，阈值设置得越高，对边缘的过滤就越严格，输出结果中的边缘线条也越发稀疏。

噪声测试

为了进一步研究在有噪声的情况下各算子的边缘检测效果，首先使用 skimage 库中的函数，对 Lena 加入高斯噪声和椒盐噪声。

img_noise1 = skimage.util.random_noise(img, mode='gaussian')
img_noise2 = skimage.util.random_noise(img, mode='s&p')

然后分别在这两张有噪声的图像上应用 Roberts 算子、Sobel 算子（水平方向）、Laplacian 算子和 Canny 算子，得到的结果如下：

其中，第一行是加入高斯噪声后各算子的输出，第二行是加入椒盐噪声后各算子的输出。

可以发现，Roberts 算子和 Sobel 算子都有一定的抗噪声能力，从图中依然可以看出部分边缘信息，而在 Laplacian 算子则对噪声非常敏感，其输出结果完全看不出任何边缘。对于 Canny 算子，需要将阈值设置得很高，才能得到比较好的效果，否则大量噪点也会被认为是边缘。经过多次尝试，最终将 threshold1 设为 180，将 threshold2 设为 3 * threshold1，得到了上图中最后一列的结果。

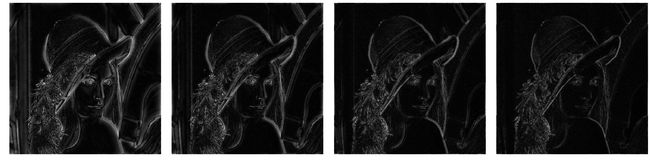
实验过程中还发现，在相同的阈值条件下，Canny 算子对高斯噪声的抵抗能力比对椒盐噪声的抵抗能力强。下图展示了当 threshold1 取值为 120、140、160、180、200 时，Canny 算子对加入了高斯噪声和椒盐噪声的图像的边缘检测效果：

HED 算法

2015年，Saining Xie 等人提出了一种基于卷积神经网络的边缘检测算法——Holistically-Nested Edge Detection（HED）算法。模型使用 VGG-16 作为骨干网络进行多尺度多层级的特征学习。其中 Holistically 的意思是“整体地”，表示该算法试图训练一个 image-to-image 的网络；Nested 则强调在生成的输出过程中，通过不断的集成和学习，得到更精确的边缘预测图。

HED 算法具有很多优点。单就预测过程来说，对一张图片进行边缘检测的速度是很快的。使用时，根据图片的实际内容，可以通过调整合适的超参数从而得到最优尺度的边缘信息。另外，由于 HED 本身就是基于神经网络的，因而可以很方便地嵌入其他网络模型中，直接参与各种学习任务的训练过程，而这点是传统边缘检测方法所不具有的。

在效果上，HED 算法也具有优越性。论文中，作者把 HED 和传统 Canny 算法进行对比。如下图所示，可以看到 HED 的效果明显优于 Canny 算法。关于 HED 算法的更多内容请参考论文原文。

代码实现

这里采用的是 HED 算法的另一个 PyTorch 实现版本，直接使用了作者提供的预训练模型进行预测。

运行结果及分析

模型在彩色 Lena 图像上的运行结果如下图所示：

在添加了高斯噪声和椒盐噪声后的图像上，运行结果分别如下所示：

添加高斯噪声后的 HED 输出图像

添加椒盐噪声后的 HED 输出图像

可见，虽然 HED 算法的边缘线条比较粗，但整体表现还是相当优秀的，尤其是在存在噪声的情况下，该算法的效果比前述几种基于微分算子的方法都要好。

总结

本文通过使用高通滤波法、微分算子法、神经网络方法三大类，共计 8 种不同的方法对 Lena 图像进行了边缘检测，将各种方法得到的结果进行横向比较，并对它们的优缺点和适用场景进行了一定的讨论。对于具有参数的算法，进一步根据参数取值的不同进行了纵向比较，观察参数对于输出结果的影响。此外，还通过对原图像添加高斯噪声和椒盐噪声进行噪声测试，研究各算法对两种噪声的敏感性。

实验结果表明，不同算法由于原理或核心函数的不同，均具有各自的优缺点和适用场景。使用时应根据图像内容和实际需求进行选择取舍，并通过调整相关参数从而到达最佳的效果。

完整源码请见 GitHub 仓库

参考资料

1. 王一丁，李琛，王蕴红.《数字图像处理》.西安电子科技大学出版社
2. Xie, Saining, and Zhuowen Tu. “Holistically-nested edge detection.” Proceedings of the IEEE international conference on computer vision. 2015.
3. PyTorch-HED：https://github.com/sniklaus/pytorch-hed
4. 互联网上的一些博客、文章、资料