CUMTOJ数据结构实验一
CUMTOJ数据结构实验一
问题 A: 子网掩码
题目描述
子网掩码是用来判断任意两台计算机的IP地址是否属于同一子网络的根据。
最为简单的理解就是两台计算机各自的IP地址与子网掩码进行AND运算后,如果得出的结果是相同的,则说明这两台计算机是处于同一个子网络上的,可以进行直接的通讯。就这么简单。
请看以下示例:
运算演示之一:
IP地址 192.168.0.1
子网掩码 255.255.255.0
转化为二进制进行运算:
IP地址 11010000.10101000.00000000.00000001
子网掩码 11111111.11111111.11111111.00000000
AND运算:
11010000.10101000.00000000.00000000
转化为十进制后为:
192.168.0.0
运算演示之二:
IP地址 192.168.0.254
子网掩码 255.255.255.0
转化为二进制进行运算:
IP地址 11010000.10101000.00000000.11111110
子网掩码 11111111.11111111.11111111.00000000
AND运算:
11010000.10101000.00000000.00000000
转化为十进制后为:
192.168.0.0
运算演示之三:
IP地址 192.168.0.4
子网掩码 255.255.255.0
转化为二进制进行运算:
IP地址 11010000.10101000.00000000.00000100
子网掩码 11111111.11111111.11111111.00000000
AND运算:
11010000.10101000.00000000.00000000
转化为十进制后为:
192.168.0.0
通过以上对三组计算机IP地址与子网掩码的AND运算后,我们可以看到它运算结果是一样的,均为192.168.0.0,所以计算机就会把这三台计算机视为在同一子网络。
输入
输入的第一行是本机IP地址;
第二行是子网掩码;
第三行是一个整数N,表示后面有N个IP地址;
接下来N行:
第1个IP地址
…
…
第N个IP地址
输出
计算并输出N个IP地址是否与本机在同一子网内。对于在同一子网的输出“INNER”,对于在不同子网的输出“OUTER”。
样例输入
192.168.0.1
255.255.255.0
3
192.168.0.2
192.168.0.254
192.168.1.2
样例输出
INNER
INNER
OUTER
思路
首先,利用scanf的特殊输入方式去除小数点,将输入的ip地址存储在数组中,然后,利用&进行与操作,最后进行比较即可
代码
#include
using namespace std;
int main() {
int local_ip[4] , subnet_mask[4] , test_ip[4];
int local_ip_subnet_mask[4] , test_ip_subnet_mask[4];
scanf("%d.%d.%d.%d" , &local_ip[0] , &local_ip[1] , &local_ip[2] , &local_ip[3]);
scanf("%d.%d.%d.%d" , &subnet_mask[0] , &subnet_mask[1] , &subnet_mask[2] , &subnet_mask[3]);
int i = 0;
while(i < 4) {
local_ip_subnet_mask[i] = local_ip[i] & subnet_mask[i];
i++;
}
int N;
cin >> N;
for(int j = 0;j < N;j++) {
scanf("%d.%d.%d.%d" , &test_ip[0] , &test_ip[1] , &test_ip[2] , &test_ip[3]);
i = 0;
while(i < 4) {
test_ip_subnet_mask[i] = subnet_mask[i] & test_ip[i];
i++;
}
int k = 0;
for(i = 0; i < 4; i++) {
if(test_ip_subnet_mask[i] != local_ip_subnet_mask[i]) {
k = 1;
cout << "OUTER" << endl;
break;
}
}
if(!k)
cout << "INNER" << endl;
}
return 0;
}
问题 B: 快来秒杀我
题目描述
根据前几次竞赛的情况,这次为了给新手们一点信心,特提供这道秒杀题来让大家杀。
ASCII码大家应该都学过了,现在给你一个很简单的任务,输入数字,表示ASCII码,输出对应的文本内容。
输入
输入的第一行是一个整数T(1<=T<=100)。
接下来输入T个正整数,这些数之间用空格、换行或Tab键来分隔。
测试数据保证输入的整数都在ASCII码范围内,并且不小于32。
输出
在一行中输出对应的文本内容。
样例输入
13
72 101 108 108 111 44
32 119 111 114 108 100 33
样例输出
Hello, world!
思路
首先,用source_num存储刚刚输入的数字,然后,立即强制将其转化成字符形式即可
代码
#include
using namespace std;
int main() {
int T = 0 , source_num;
cin >> T;
int tmp = 0;
for(; tmp < T; tmp++) {
cin >> source_num;
cout << (char)(source_num);
}
return 0;
}
问题 C: 最短路径1
题目描述
有n个城市m条道路(n<1000, m<10000),每条道路有个长度,请找到从起点s到终点t的最短距离和经过的城市名。
输入
输入包含多组测试数据。
每组第一行输入四个数,分别为n,m,s,t。
接下来m行,每行三个数,分别为两个城市名和距离。
输出
每组输出占两行。
第一行输出起点到终点的最短距离。
第二行输出最短路径上经过的城市名,如果有多条最短路径,输出字典序最小的那条。若不存在从起点到终点的路径,则输出“can’t arrive”。
样例输入
3 3 1 3
1 3 3
1 2 1
2 3 1
样例输出
2
1 2 3
思路
首先,利用while循环输入n m s t,然后,利用一个队列存储城市名及其间距,最后利用Dijkstra算法求出最短路径
代码
#define _CRT_SECURE_NO_WARNINGS
#include
#include
#include
#include
#include
#include
#include
#include 问题 D: 二叉排序树
题目描述
输入一系列整数,建立二叉排序数,并进行前序,中序,后序遍历。
输入
输入第一行包括一个整数n(1<=n<=100)。接下来的一行包括n个整数。
输出
可能有多组测试数据,对于每组数据,将题目所给数据建立一个二叉排序树,并对二叉排序树进行前序、中序和后序遍历。每种遍历结果输出一行。每行最后一个数据之后有一个空格。
样例输入
1
2
2
8 15
4
21 10 5 39
样例输出
2
2
2
8 15
8 15
15 8
21 10 5 39
5 10 21 39
5 10 39 21
思路
首先,将输入的数据建立一棵二叉排序树,然后,进行前序、中序、后序遍历即可
代码
#include
using namespace std;
struct node {
int data;
node *left , *right;
};
void insert(node* &root , int x) {
if (root == NULL) {
root = new node;
root->data = x;
root->left = root->right = NULL;
}
else if (x == root->data)
return;
else if (x < root->data)
insert(root->left , x);
else
insert(root->right , x);
}
void preorder(node* root) {
if (root == NULL)
return;
cout << root->data << " ";
preorder(root->left);
preorder(root->right);
}
void inorder(node* root) {
if (root == NULL)
return;
inorder(root->left);
cout << root->data << " ";
inorder(root->right);
}
void postorder(node* root) {
if (root == NULL)
return;
postorder(root->left);
postorder(root->right);
cout << root->data << " ";
}
int main() {
int n , x;
while (cin >> n) {
node *root = NULL;
for (int i = 0; i < n; i++) {
cin >> x;
insert(root , x);
}
preorder(root);
cout << endl;
inorder(root);
cout << endl;
postorder(root);
cout << endl;
}
return 0;
}
知识延伸
- 二叉排序树或者是一棵空树,或者是具有下列性质的二叉树:
(1)若左子树不空,则左子树上所有节点的值均小于它的根节点的值;
(2)若右子树不空,则右子树上所有节点的值均大于它的根节点的值;
(3)左、右子树也分别为二叉排序树;
(4)没有键值相等的节点。 - 前序、中序、后序
-
前序遍历(根–>左–>右)
(1) 访问根节点 (2) 前序遍历左子树 (3) 前序遍历右子树 -
中序遍历(根–>左–>右)
(1)中序遍历左子树 (2) 访问根节点 (3) 中序遍历右子树 -
后序遍历(根–>左–>右)
(1) 后序遍历左子树 (2) 后序遍历右子树 (3) 访问根节点
问题 E: 密码锁
题目描述
玛雅人有一种密码,如果字符串中出现连续的2012四个数字就能解开密码。给一个长度为N的字符串,(2= 第一行输入N,第二行输入N个数字,只包含0,1,2 5 1 首先,利用一个双端队列record记录输入的输入的012字符串,然后,比较即可 快速排序是对起泡排序的一种改进。它的基本思想是,通过一趟排序将待排序的记录分割成两个独立的部分,其中一部分记录的关键字均比另一部分的关键字小,在分成两个部分之后则可以分别对这两个部分继续进行排序,从而使整个序列有序。 输入的第一行包含1个正整数n,表示共有n个整数需要参与排序。其中n不超过100000。 只有1行,包含n个整数,表示从小到大排序完毕的所有整数。 10 1 2 3 4 5 6 7 8 9 10 在本题中,需要按照题目描述中的算法完成快速排序的算法。 快速排序是一种十分常用的排序算法,其平均时间复杂度为O(knlnn),其中n为待排序序列中记录的个数,k为常数。大量的实际应用证明,在所有同数量级的此类排序算法中,快速排序的常数因子k是最小的,因此,就平均时间而言,快速排序是目前被认为最好的一种内部排序方法。 而在C语言的常用编译器中,qsort函数是一个非常常用的快速排序函数。 首先,利用一个大数组存储输入的待排序数字,然后,利用qsort函数进行处理,最后,输出即可。 qsort函数包含在 qsort函数声明如下: void qsort(void * base,size_t nmemb,size_t size ,int(*compar)(const void *,const void *)); 参数说明: 折半插入排序同样是一种非常简单的排序方法,它的基本操作是在一个已经排好序的有序表中进行查找和插入。不难发现这个查找的过程可以十分自然的修改成折半查找的方式进行实现。 输入的第一行包含1个正整数n,表示共有n个整数需要参与排序。其中n不超过1000。 只有1行,包含n个整数,表示从小到大排序完毕的所有整数。 10 1 2 3 4 5 6 7 8 9 10 在本题中,需要按照题目描述中的算法完成折半插入排序的算法。与直接插入排序算法不同,折半插入排序算法在查找插入位置时采用了折半查找的方案,减少了关键字之间的比较次数,但是记录的移动次数并没有发生改变,因此折半插入排序的时间复杂度依旧为O(n2),同样不是一种非常高效的排序方法。 首先,利用一个大数组arr存储输入的待排序数字,然后,调用BInsertSort函数进行处理,最后,输出即可。 最小生成树问题是实际生产生活中十分重要的一类问题。假设需要在n个城市之间建立通信联络网,则连通n个城市只需要n-1条线路。这时,自然需要考虑这样一个问题,即如何在最节省经费的前提下建立这个通信网。 输入的第一行包含一个正整数n,表示图中共有n个顶点。其中n不超过50。 只有一个整数,即最小生成树的总代价。请注意行尾输出换行。 4 6 在本题中,需要掌握图的深度优先遍历的方法,并需要掌握无向图的连通性问题的本质。通过求出无向图的连通分量和对应的生成树,应该能够对图的连通性建立更加直观和清晰的概念。 首先,利用GetM()函数将邻接矩阵输入并存储在Arrow结构体中,然后,调用MiniSpanTree()函数生成最小生成树,最后,运算并输出最小生成树的代价。 Hacker Bill has accidentally lost all the information from his workstation’s hard drive and he has no backup copies of its contents. He does not regret for the loss of the files themselves, but for the very nice and convenient directory structure that he had created and cherished during years of work. Fortunately, Bill has several copies of directory listings from his hard drive. Using those listings he was able to recover full paths (like “WINNT\SYSTEM32\CERTSRV\CERTCO~1\X86”) for some directories. He put all of them in a file by writing each path he has found on a separate line. Your task is to write a program that will help Bill to restore his state of the art directory structure by providing nicely formatted directory tree. The first line of the input file contains single integer number N (1 <= N <= 500) that denotes a total number of distinct directory paths. Then N lines with directory paths follow. Each directory path occupies a single line and does not contain any spaces, including leading or trailing ones. No path exceeds 80 characters. Each path is listed once and consists of a number of directory names separated by a back slash (""). Each directory name consists of 1 to 8 uppercase letters, numbers, or the special characters from the following list: exclamation mark, number sign, dollar sign, percent sign, ampersand, apostrophe, opening and closing parenthesis, hyphen sign, commercial at, circumflex accent, underscore, grave accent, opening and closing curly bracket, and tilde ("!#$%&’()-@^_`{}~"). Write to the output file the formatted directory tree. Each directory name shall be listed on its own line preceded by a number of spaces that indicate its depth in the directory hierarchy. The subdirectories shall be listed in lexicographic order immediately after their parent directories preceded by one more space than their parent directory. Top level directories shall have no spaces printed before their names and shall be listed in lexicographic order. See sample below for clarification of the output format. 7 GAMES输入
输出
样例输入
02120样例输出
思路
代码
#include 知识延伸
string的子串:
string substr(int pos = 0,int n = npos) const;//返回pos开始的n个字符组成的字符串
string的交换:
void swap(string &s2); //交换当前字符串与s2的值
函数原型:void *memset(void *s , int ch , size_t n )
函数解释:将s中的前n个字节用ch替换并且返回s
函数作用:在一段内存块中填充某一个给定的值,常用于较大的对结构体和数组的清零操作。
void push_front(const T& x):双端队列头部增加一个元素x
void push_back(const T& x):双端队列尾部增加一个元素x
void pop_front():删除双端队列中最前一个元素
void pop_back():删除双端队列中最后一个元素
void clear():清空双端队列中最后一个元素
void swap(deque&):交换两个同类型向量的数据问题 F: 算法10-6~10-8:快速排序
题目描述
快速排序的算法可以描述如下:

在本题中,读入一串整数,将其使用以上描述的快速排序的方法从小到大排序,并输出。输入
第二行包含n个用空格隔开的正整数,表示n个需要排序的整数。输出
请在每个整数后输出一个空格,并请注意行尾输出换行。样例输入
2 8 4 6 1 10 7 3 5 9样例输出
提示
思路
代码
#include 知识延伸
base,要排序的数组
nmemb,数组中元素的数目
size,每个数组元素占用的内存空间,可使用sizeof函数获得问题 G: 算法10-2:折半插入排序
题目描述
折半插入排序的算法可以描述如下:
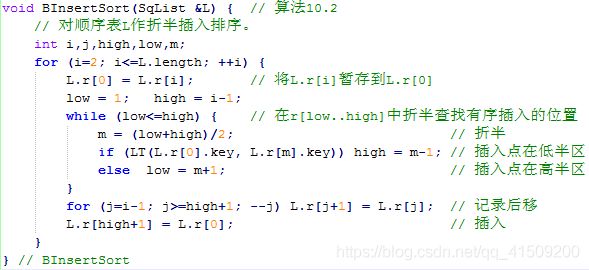
在本题中,读入一串整数,将其使用以上描述的折半插入排序的方法从小到大排序,并输出。输入
第二行包含n个用空格隔开的正整数,表示n个需要排序的整数。输出
请在每个整数后输出一个空格,并请注意行尾输出换行。样例输入
2 8 4 6 1 10 7 3 5 9样例输出
提示
思路
代码
#include问题 H: 算法7-9:最小生成树
题目描述
可以用连通网来表示n个城市以及n个城市之间可能设置的通信线路,其中网的顶点表示城市,边表示两个城市之间的线路,赋于边的权值表示相应的代价。对于n个顶点的连通网可以建立许多不同的生成树,每一棵生成树都可以是一个通信网。现在,需要选择一棵生成树,使总的耗费最小。这个问题就是构造连通网的最小代价生成树,简称最小生成树。一棵生成树的代价就是树上各边的代价之和。
而在常用的最小生成树构造算法中,普里姆(Prim)算法是一种非常常用的算法。以下是其算法的大致结构:

在本题中,读入一个无向图的邻接矩阵(即数组表示),建立无向图并按照以上描述中的算法建立最小生成树,并输出最小生成树的代价。输入
以后的n行中每行有n个用空格隔开的整数,对于第i行的第j个整数,如果不为0,则表示第i个顶点和第j个顶点有直接连接且代价为相应的值,0表示没有直接连接。当i和j相等的时候,保证对应的整数为0。
输入保证邻接矩阵为对称矩阵,即输入的图一定是无向图,且保证图中只有一个连通分量。输出
样例输入
0 2 4 0
2 0 3 5
4 3 0 1
0 5 1 0样例输出
提示
思路
代码
#include 问题 I: 8.5.11 Disk Tree
题目描述
输入
输出
样例输入
WINNT\SYSTEM32\CONFIG
GAMES
WINNT\DRIVERS
HOME
WIN\SOFT
GAMES\DRIVERS
WINNT\SYSTEM32\CERTSRV\CERTCO~1\X86样例输出
DRIVERS
HOME
WIN
SOFT
WINNT
DRIVERS
SYSTEM32
CERTSRV
CERTCO~1
X86
CONFIG提示
思路
代码
#include