中国邮路算法（中国邮递员问题）（详细）

通路：在无向图中由点边交替组成的序列就是通路（如果这个图是简单的，那么也可以使用点的序列来表示），如果首尾的点相同，则称为一条回路
无向图的连通性：无向图中任意一对点之间均有通路
欧拉通路：从某个顶点出发，将所有的边遍历一遍并且仅经过一遍的通路序列称为欧拉通路，连通的多重图有欧拉回路而无欧拉回路当且仅当它恰有两个奇数度顶点
这里说明了欧拉通路的条件：

图是连通的，没有孤立节点
对于无向图来说，奇数度的顶点为2个，这两个顶点分别是起点以及终点（0个的话就是回路了）
欧拉回路：如果欧拉通路的起点与终点一样，则成为欧拉回路， 连通的多重图具有欧拉回路当且仅当它的每个顶点都有偶数度
则欧拉回路的条件：

图是连通的，没有孤立节点
无向图的每个节点的度数都是偶数度，有向图每个节点的入度等于出度
判断图是否存在欧拉回路
根据判断的条件，首先是判断图的连通性，然后判断图的每个节点的度数是否是偶数就可以了：

开始还要判断是否是欧拉回路。因为这个程序主要是针对欧拉回路的。
因为图中奇度顶点组合成4条边的情形有很多种，所以要分别求出每种组合形成的边的代价，然后从中选出代价最小的边。
另外，在此问题中，边的“添加”的应该理解为从一个奇度点到另一个奇度点之间的路径。
“邮递员”问题的算法描述如下:
（1） 建立街区无向网的邻接矩阵；
（2） 求各顶点的度数；
（3） 求出所有奇度点；
（4） 求出每一个奇度点到其它奇度点的最短路径；
（5） 找出距离最短的添加方案；
（6） 根据最佳方案添加边，对图进行修改，使之满足一笔画的条件；
（7） 对图进行一笔画，并输出；

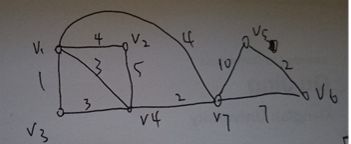
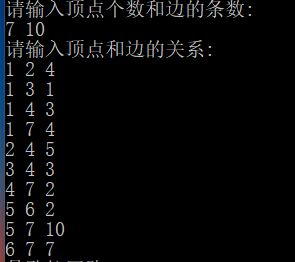
程序首先输入点与边，和点与边的关系，读取结点个数和边条数以及点与点间的连通关系，并建立街区无向网的邻接矩阵，同时记录各结点度数。
随后遍历各结点，找出其中所有的奇点。如果奇点个数大于2，则需要加边来使奇点数为0；如果奇点正好为两个，则从其中一个点出发，到另一点结束能形成欧拉图，但是不能形成回路，也不能保证从邮局出发；如果奇点数为0，则可以形成欧拉回路。接下来分情况讨论：
当奇点数大于2的时候：通过Floyd算法求任意两点路径的最短距离，并将读入的图的数据更新为最短路径。随后进入extend_edge()函数。通过标记的方法来加边。当某一边的始点与终点均为奇点，并且两点间可连通时，将需要加边的始点和终点以及距离信息存入odd_edge中。随后通过一个深度遍历，判断需要加的边是否为最短的，即确定距离最短的添加方案。随后用dijkstra算法确定从该始点到终点的最短路径。
当奇点数等于2的时候，判断起始点能否为1，若可以，则设置first_id = 1即可。若不能，则无法构成环路。

#include 
#include 
#include 

#define min(a,b) ( (a) < (b) ? (a) : (b) )
#define MAX_NODE 100
#define MAX_EDGE 100
#define INF 0x7fffffff      // 表示两点不连通
int degree[1005];
int tree[1005];

typedef struct
{
    int number;   // 标记位
    int cost;     // 结点间距
    int dis;      // 结点最近距离
}Node;

typedef struct
{
    int from;     // 边起点
    int to;       // 边终点
    int dis;      // 边距离
}Edge;

int n, m;                              // 点的个数和边的个数
int total_edge, odd_point;             // 总边数和奇点数
Node map[MAX_NODE][MAX_NODE];          // 结点连接情况
int point[MAX_NODE];                   // 每个结点的度数
int need_add_num, min_count, edge_num; // 需要添加边的个数
Edge odd_edge[MAX_EDGE];
int point_flag[MAX_EDGE];
int min_edge[MAX_EDGE];
int tmp_edge[MAX_EDGE];
int top;
int finish_flag = 0;
int path_stack[MAX_EDGE];

int findroot(int x){               //并查集的方式判断图连通性
    if(tree[x]==-1)
        return x;
    else{
        int temp = findroot(tree[x]);
        tree[x] = temp;
        return temp;
    }
}

void Floyd()
{
    // 比较i到j直达近还是从i到k加上k到j近。添加的结点k放在最外层循环。
    int i,j,k;
    for (k = 1; k <= n; k++)
        for (i = 1; i <= n; i++)
            if(map[i][k].dis != INF)
            {
                for (j = 1; j < n; j++)
                    if(map[k][j].dis != INF)
                    {
                        map[i][j].dis = map[j][i].dis = min(map[i][j].dis, map[i][k].dis + map[k][j].dis);
                    }
            }
}

void search_edge(int count, int step)
{
    // 深度还是广度遍历寻找最优方案
    // step用于记录数量，count记录最短长度
    // 寻找路径存入了数组中，可通过i访问

    int i;
    if (step == need_add_num)
    {
        if (count < min_count)
        {
            for (i = 0; i < need_add_num; i++)
            {
                min_edge[i] = tmp_edge[i];
            }
            min_count = count;
        }
        return;
    }
    int a, b, c;
    for (i = 0; i < edge_num; i++)
    {
        a = odd_edge[i].from;
        b = odd_edge[i].to;
        c = odd_edge[i].dis;
        if (point_flag[a] == 1 && point_flag[b] == 1)
            // 如果两点均未相连
        {
            point_flag[a] = point_flag[b] = 0;    // 置标记位为0
            tmp_edge[step] = i;
            search_edge(count + c, step + 1);
            point_flag[a] = point_flag[b] = 1;
        }
    }
}

void dijkstra_to_add_edge(int s, int e)
{
    int i;
    int dis[MAX_NODE];       // 点到起始（s）点的距离
    int used[MAX_NODE];      // 标记位
    int pre[MAX_NODE];       // 记录其从哪一点过来的，方便回溯

    memset(used, 0, sizeof(used));   // 初始化一波
    for (i = 1; i <= n; i++)
    {
        dis[i] = INF;
    }
    dis[s] = 0;

    while (1)
    {
        int v = -1;
        for ( i = 1; i <= n; i++)
        {
            if (!used[i] && (v == -1 || dis[i] < dis[v]))
            {
                v = i;
            }
        }
        if (v == e || v == -1)
        // 当当前点是末点e时或本身v就是最小时
            break;
        used[v] = 1;    // 修改标记位
        for (i = 1; i <= n; i++)
        {
            if (map[v][i].cost < INF && (dis[v] + map[v][i].cost) < dis[i])
            {
                pre[i] = v;
                dis[i] = dis[v] + map[v][i].cost;
            }
        }
    }

    int v = e;
    int pre_node = e;
    while (pre_node != s)
    {
        pre_node = pre[v];
        ++map[pre_node][v].number;    // 加边
        ++map[v][pre_node].number;
    }
}


void extend_edge(int add_num)
{
    int i,j;
    need_add_num = add_num;
    memset(point_flag, 0, sizeof(point_flag));
    edge_num = 0;

    // 当两个点都是奇点的时候
    for (i = 1; i < n; i++)
    {
        if ((point[i] & 0x1) == 1)
        {
            for (j = i+1; j <= n; j++)
            {
                if ((point[j] & 0x1) == 1 && map[i][j].dis < INF)
                {
                    point_flag[i] = point_flag[j] = 1;   // 将i，j两点标记为需要被连接的奇点
                    odd_edge[edge_num].from = i;         // 将相关信息存入odd_edge数组中
                    odd_edge[edge_num].to = j;
                    odd_edge[edge_num].dis = map[i][j].dis;
                    edge_num++;
                }
            }
        }
    }

    min_count = INF;    // 设置最小值，方便比较
    search_edge(0, 0);
    if (min_count < INF)
    {
        int a, b;
        for (i = 0; i < need_add_num; i++)
        {
            int k = min_edge[i];
            a = odd_edge[k].from;
            b = odd_edge[k].to;
            dijkstra_to_add_edge(a, b);   // 用dijkstra算法求加边后两点最短距离
            point[a] = point[b] = 0;
        }
        odd_point -= add_num * 2;
        total_edge += add_num;
    }
    else
    {
        exit(-1);
    }

}

void search_euler_path(int s)
{
    int i;
    for (i = 1; i <= n; i++)
    {
        if (map[s][i].number > 0)
        {
            --map[s][i].number;
            --map[i][s].number;
            path_stack[top++] = i;
            if (top == (total_edge + 1))
                // 结点比总边数多1
            {
                finish_flag = 1;
                return;
            }

            search_euler_path(i);
            if (finish_flag)
                return;
            ++map[s][i].number;
            ++map[i][s].number;
            --top;
        }
    }
}


int main()
{
    int i,j;

    printf("请输入顶点个数和边的条数:\n");

    while (scanf("%d %d", &n, &m) != EOF)
    {
        memset(tree, -1, sizeof(tree));
        memset(degree, 0, sizeof(degree));
        // 初始化
        memset(point, 0, sizeof(point));
        for (i = 1; i <= n; i++)
            for (j = 1; j <= n; j++)
                map[i][j].cost = map[i][j].dis = INF;
        total_edge = 0;

        // 读入图的数据
        printf("请输入顶点和边的关系:\n");
        int a, b, c;
        for (i = 0; i < m; i++)
        {
            scanf("%d %d %d", &a, &b, &c);
            int tempa = findroot(a);
            int tempb = findroot(b);
            if(tempa != tempb)
                tree[tempa] = tempb;
            degree[a]++;                //无向图记录度数
            degree[b]++;
            map[a][b].cost = map[b][a].cost = c;
            map[a][b].dis = map[b][a].dis = c;
            map[a][b].number = map[b][a].number = 1;
            ++point[a];
            ++point[b];
            ++total_edge;
        }

        int flag = 0;
        int ans = 0;
        for(i=1; i<= n; i++){     //判断连通性
            if(tree[i]==-1)
                ans++;
        }
        for( i=1; i<=n; i++){    //判断度数
            if(degree[i]%2){
                flag = 1;
                break;
            }
        }
        if(ans > 1 || flag)
            {
                printf("不是欧拉回路\n");
                return 0;
            }
        else
            printf("是欧拉回路\n");
        odd_point = 0;
        for ( i = 1; i <= n; i++)
            // 判断点是否为奇点
        {
            if ((point[i] & 0x1) == 1)
            {
                odd_point++;
            }
        }

        int first_id = 1;    // 设置邮局的位置 1即为A
        if (odd_point > 2)
            // 奇点个数大于两个的时候，用floyd算法更新任意两点之间最短路径，并且添加边
        {
            Floyd();
            extend_edge(odd_point / 2);
            // 两个奇点添加一条边，共需要添加odd_point/2条边
        }

        top = 0;
        if (odd_point == 2)
            // 奇点个数为2的时候，从一个奇点出发到另一个奇点去，但不能构成环路，直接退出程序
        {
            for (i = 1; i <= n; i++)
            {
                if ((point[i] & 0x1) == 1)
                {
                    first_id = i;
                    break;
                }

            }
            if (first_id != 1)
            {
                exit(-2);
            }
        }

        path_stack[top++] = first_id;
        // 利用栈进行深度搜索来确定最短路线并存入数组
        search_euler_path(first_id);

        char vex;
        // 将最短路线输出
        for (i = 0; i <= total_edge; i++)
        {
            vex = path_stack[i] + 'A' - 1;
            printf("%c", vex);
            if (i < total_edge)
            {
                printf("->");
            }
        }
        printf("\n");
    }

    return 0;
}