CSU 1811 Tree Intersection(线段树+启发式合并 解法)
转自:http://m.blog.csdn.net/hackertom/article/details/71304826
Problem
acm.csu.edu.cn/csuoj/problemset/problem?pid=1811
vjudge.net/contest/161962#problem/I
Reference
blog.csdn.net/qwb492859377/article/details/52436186
www.cnblogs.com/fightfordream/p/6801852.html
Meaning
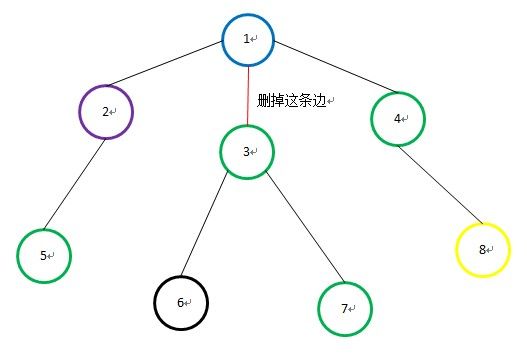
一棵 n 个结点的树,每个结点都有一种颜色,问对与树上的每条边,删掉它之后得到的两棵树中,共有的颜色有多少种(在那两棵树中都有的颜色就是公有的颜色)
Analysis
首先规定 1 号结点为整棵树的根(其它号也可以)。
对与每一条边,就看成是某个结点于它的父结点的连边,于是,删掉这条边后两个连同块的共有颜色数,就等价于以这个结点为根的子树里共有颜色数(只有两个连通块,其中一个连通块的“公共颜色”即是两个连同块的公共颜色)。
公共颜色是什么呢?假如在其中一个连通块中有 2 个绿色结点,而原树一共有 4 个结点是绿色的,那绿色就是这两个连通块的公共颜色之一;反之,这个连通块有一个黑色结点,而原树也总共只有一个黑色结点,那黑色就是这个连通块“私有”的颜色。
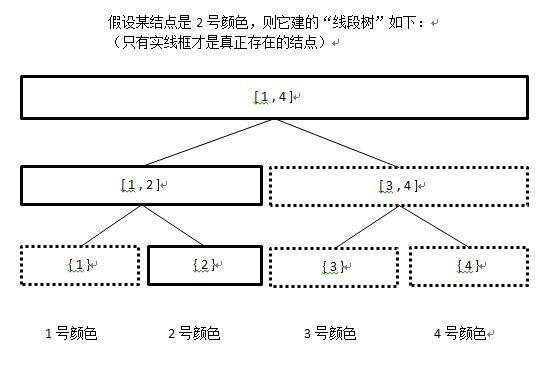
怎么统计一棵子树里的共有颜色数呢?可以用线段树。先不考虑空间,对每个结点都建一棵线段树,记录共有颜色数,然后将所有子结点的树合并到父结点的树里,就得到了父结点的答案。但这么做空间太大。
但其实对每个结点都没必要真的建一整棵树,因为根结点只有一种颜色,只需要一条链,而子树的信息,可以重用子树建出来的结点,这样就可以开得下。
具体看代码理解吧,线段树新姿势啊。
PS:我自己再补充一下吧,感觉这个建树和结构已经与主席树非常的像了。
Code
#include #include using namespace std; const int N = 100000; struct edge { int to, nxt; } e[N<<1]; struct node { int lc, rc; // 左、右子结点的位置 int com; // 这棵树中共有颜色的数量 int num; // 对叶子有用,表示这棵树中这种颜色的结点数 } tree[18*N]; // 存树结点的空间 int sz; // 树结点总数 int c[N+1]; // 结点i的颜色 int sum[N+1]; // 颜色i的总数 int head[N+1]; // 前向星链头 int root[N+1]; // 为第i个结点建的线段树的根所在位置 int ans[N]; // 答案数组 void add_edge(int f, int t, int id) { e[id].to = t; e[id].nxt = head[f]; head[f] = id; } inline void pushup(int x) { /* 不是叶子的结点,只需记录共有颜色的数量 */ tree[x].com = tree[tree[x].lc].com + tree[tree[x].rc].com; } int build(int c, int l, int r) { int rt = ++sz; tree[rt].lc = tree[rt].rc = tree[rt].num = 0; if(l == r) { tree[rt].num = 1; tree[rt].com = tree[rt].num < sum[c]; } else { int m = l + r >> 1; /* 不需要建整棵树,只要建一条链 */ if(c > m) tree[rt].rc = build(c, m+1, r); else tree[rt].lc = build(c, l, m); pushup(rt); } return rt; } void merge(int &fa, int ch, int l, int r) { if(!fa || !ch) { /* 若父结点那棵线段树的这个结点为空, * 就直接重用子结点的线段树的这条链 */ if(!fa) fa = ch; return; } if(l != r) { int m = l + r >> 1; merge(tree[fa].lc, tree[ch].lc, l, m); merge(tree[fa].rc, tree[ch].rc, m+1, r); pushup(fa); } else { /* 将子树里这种颜色的结点数加到父结点的树 */ tree[fa].num += tree[ch].num; /* 这种颜色的结点不全在这棵树中, * 则这种颜色是共有颜色 */ tree[fa].com = tree[fa].num < sum[l]; } } void dfs(int rt, int fa, int eid, int n) { /* 先给根结点“建棵树” */ root[rt] = build(c[rt], 1, n); for(int i=head[rt]; ~i; i=e[i].nxt) { if(e[i].to == fa) continue; /* 先递归处理子结点 */ dfs(e[i].to, rt, i, n); /* 然后将子结点信息合并上来 */ merge(root[rt], root[e[i].to], 1, n); } /* 加边时同一条边加了两次, * 这个映射找出此边在输入时的序号 */ if(rt != 1) ans[eid/2+1] = tree[root[rt]].com; } int main() { tree[0].lc = tree[0].rc = tree[0].com = tree[0].num = 0; int n; while(~scanf("%d", &n)) { memset(sum, 0, sizeof sum); for(int i=1; i<=n; ++i) { scanf("%d", c+i); ++sum[c[i]]; } memset(head, -1, sizeof head); for(int i=1, a, b, id=0; i