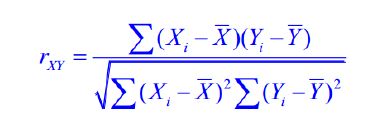机器学习（四）一元线性回归
线性回归
一元线性回归（单特征）
h θ ( x ) = θ 0 + θ 1 x h_\theta(x) = \theta_0+\theta_1x hθ(x)=θ0+θ1x
这个方程对于的图像是一条直线，称为回归线。其中 θ 1 \theta_1 θ1为回归线的斜率， θ 0 \theta_0 θ0为回归线的截距
代价函数（损失函数）
- 最小二乘法计算误差
J ( θ 0 , θ 1 ) = 1 / 2 m ∑ i = 1 m ( y i − h θ ( x i ) ) 2 J(\theta_0,\theta_1) = 1/2m\sum_{i=1}^{m} {(y^i-h_\theta(x^i))^2} J(θ0,θ1)=1/2mi=1∑m(yi−hθ(xi))2
- y y y 为真实值，预测值为 h θ ( x ) h_\theta(x) hθ(x)误差平方为 ( y − h θ ( x ) ) 2 (y-h_\theta(x))^2 (y−hθ(x))2
2.寻找合适的参数，使得误差平方和最小。
3.代码实现
#最小二乘法 b为截距 k为斜率
def compute_error(b, k, x_data, y_data):
totalError = 0
for i in range(0,len(x_data)):
totalError += (y_data[i] - (k * x_data[i] + b)) ** 2
return totalError / float(len(x_data)) / 2.0
- 相关系数
衡量线性相关性的强弱 - 决定系数
用来描述非线性或者两个及两个以上自变量的相关关系强弱
梯度下降法求解
- 原理：不断改变 θ 0 , θ 1 \theta_0,\theta_1 θ0,θ1直到 J ( θ 0 , θ 1 ) J(\theta_0,\theta_1) J(θ0,θ1)到达一个全局最小值，或者局部最小值
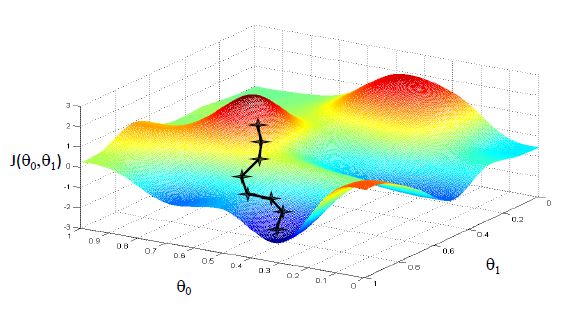
- 求法
θ j : = θ j − α ∂ ∂ θ j J ( θ 0 , θ 1 ) \theta_j: = \theta_j-\alpha\frac {\partial} {\partial\theta_j}J(\theta_0,\theta_1) θj:=θj−α∂θj∂J(θ0,θ1)
( f o r j = 1 a n d j = 0 ) (for j = 1 and j = 0) (forj=1andj=0)
其中偏导部分的求法：
∂ ∂ θ j J ( θ 0 , θ 1 ) = \frac {\partial} {\partial\theta_j}J(\theta_0,\theta_1)= ∂θj∂J(θ0,θ1)=
j = 0 : ∂ ∂ θ 0 J ( θ 0 , θ 1 ) = 1 m ∑ i = 1 m ( h θ ( x i ) − y i ) j = 0: \frac {\partial} {\partial\theta_0}J(\theta_0,\theta_1)=\frac {1} {m}\sum_{i=1}^{m} {(h_\theta(x^i)-y^i)} j=0:∂θ0∂J(θ0,θ1)=m1i=1∑m(hθ(xi)−yi)
j = 1 : ∂ ∂ θ 1 J ( θ 0 , θ 1 ) = 1 m ∑ i = 1 m ( h θ ( x i ) − y i ) . x i j = 1: \frac {\partial} {\partial\theta_1}J(\theta_0,\theta_1)=\frac {1} {m}\sum_{i=1}^{m} {(h_\theta(x^i)-y^i).x^i} j=1:∂θ1∂J(θ0,θ1)=m1i=1∑m(hθ(xi)−yi).xi
- 实现代码
# learning rate
lr = 0.0001
#截距
b = 0
#斜率
k = 0
#最大迭代次数
epochs = 50
#梯度下降法求 b 和 k
def gradient_descent_runner(x_data, y_data, b, k, lr, epochs):
# 计算总数据量
m = float(len(x_data))
# 循环epochs次
for i in range(epochs):
b_grad = 0
k_grad = 0
# 计算梯度的总和再求平均
for j in range(0, len(x_data)):
b_grad += (1/m) * (((k * x_data[j]) + b) - y_data[j])
k_grad += (1/m) * x_data[j] * (((k * x_data[j]) + b) - y_data[j])
# 更新b和k
b = b - (lr * b_grad)
k = k - (lr * k_grad)
# 每迭代5次，输出一次图像
if i % 5==0:
print("epochs:",i)
plt.plot(x_data, y_data, 'b.')
plt.plot(x_data, k*x_data + b, 'r')
plt.show()
return b, k
利用sklearn库求解
利用 sklearn库中的 LinearRegression（线性回归）函数
from sklearn.linear_model import LinearRegression#导入线性回归函数
import numpy as np
import matplotlib.pyplot as plt
# 创建并拟合模型
model = LinearRegression()
model.fit(x_data, y_data)
# 画图
plt.plot(x_data, y_data, 'b.')
plt.plot(x_data, model.predict(x_data), 'r')
plt.show()