算法训练赛第七场
算法训练赛第七场
链接
文章目录
- 算法训练赛第七场
- A [计蒜客 A1638 合并数字](https://nanti.jisuanke.com/t/A1638)
- B [计蒜客 A2238 找质数](https://nanti.jisuanke.com/t/A2238)
- C [HDU 1312 Red and Black](http://acm.hdu.edu.cn/showproblem.php?pid=1312)
- D [CodeForces 1141A Game 23](http://codeforces.com/problemset/problem/1141/A)
- E [POJ 1321 棋盘问题](http://poj.org/problem?id=1321)
- F [HDU 1087 Super Jumping!](http://acm.hdu.edu.cn/showproblem.php?pid=1087)
- G [HDU 2161 Primes](http://acm.hdu.edu.cn/showproblem.php?pid=2161)
- H [CodeForces 1311B WeirdSort](http://codeforces.com/problemset/problem/1311/B)
- I [LightOJ 1078 Integer Divisibility](https://vjudge.net/problem/LightOJ-1078/origin)
- J [HDU 1969 Pie](http://acm.hdu.edu.cn/showproblem.php?pid=1969)
- K [HDU 1263 水果](http://acm.hdu.edu.cn/showproblem.php?pid=1263)
- L [CodeForces 1315A Dead Pixel](http://codeforces.com/problemset/problem/1315/A)
- M [HDU 1211 Complete the Sequence](http://acm.hdu.edu.cn/showproblem.php?pid=1121)
- N [LightOJ 1234 Harmonic Number](http://lightoj.com/login_main.php?url=volume_showproblem.php?problem=1234)
A 计蒜客 A1638 合并数字
蒜头君得到了 n 个数,他想对这些数进行下面这样的操作,选出最左边的相邻的差的绝对值为 11 的两个数,只保留较小的数,删去较大的数,直到没有两个相邻的差的绝对值为 11 的数,问最多可以进行多少次这样的操作?
每次比较最左边两个数,并进行删除操作 首先想到栈
-
每次读入临时变量
tmp进行判断并执行操作 -
若栈不为空,则进行大小比较
-
若栈顶元素比临时变量大1
-
将栈顶删除 即执行出栈
-
计数器
cnt进行加1 -
执行一次后,栈顶进行更新,要将
tmp与新的栈顶进行比较
-
- 若临时变量比栈顶元素大1
- 计数器
cnt进行加1
- 计数器
- 若上述均不满足 进行入栈即可
-
-
最终输出 计数结果
#includeB 计蒜客 A2238 找质数
一天蒜头君猜想,是不是所有的偶数(除了 2),都可以用两个质数相加得到呢?于是聪明的蒜头君就找你来验证了。
毒瘤题,数据量有问题
熟悉一下快读和欧拉筛
#include C HDU 1312 Red and Black
There is a rectangular room, covered with square tiles. Each tile is colored either red or black. A man is standing on a black tile. From a tile, he can move to one of four adjacent tiles. But he can’t move on red tiles, he can move only on black tiles.
DFS or BFS模板题
-
dfs
#include#include using namespace std; int n, m, startx, starty, cnt; int nt_sp[4][2] = {-1,0,1,0,0,1,0,-1}; char str[25][25]; bool det[25][25]; bool bdy(int x, int y){ return (x <= n && x >= 1 && y <= m && y >= 1); } void dfs(int x,int y){ cnt++; det[x][y] = true; for(int i = 0;i<4;i++){ int nx = x + nt_sp[i][0], ny = y + nt_sp[i][1]; if(!det[nx][ny] && bdy(nx, ny) && str[nx][ny] == '.') dfs(nx,ny); } } int main(){ while(scanf("%d %d",&m,&n)){ if(m == 0 && n == 0) break; cnt = 0; memset(det,0,sizeof det); for(int i = 1;i<=n;i++){ for(int j = 1;j<=m;j++){ scanf(" %c",&str[i][j]); if(str[i][j] == '@'){ startx = i,starty = j; } } } dfs(startx,starty); printf("%d\n",cnt); } return 0; } -
bfs
#include#include #include #define ios ios::sync_with_stdio(false);cin.tie(0);cout.tie(0); using namespace std; int n, m, bx, by, cnt, nx, ny; char str[25][25]; bool det[25][25]; int nt_sp[4][2] = {-1,0,1,0,0,1,0,-1}; struct node{ int x, y; }; queue <node> q; bool bdy(int x, int y){ return (x <= n && x >= 1 && y <= m && y >= 1); } void bfs(int x ,int y){ while(!q.empty()) q.pop(); det[x][y] = true; q.push({x, y}); while (!q.empty()){ node now = q.front(); for (int i = 0; i < 4; i ++){ nx = now.x + nt_sp[i][0], ny = now.y + nt_sp[i][1]; if(!det[nx][ny] && bdy(nx, ny) && str[nx][ny] == '.'){ cnt ++; det[nx][ny] = true; q.push({nx,ny}); } } q.pop(); } } int main(){ ios; while (cin >> m >> n && m && n){ cnt = 1; memset(det, false, sizeof det); for (int i = 1; i <= n; i ++) for (int j = 1; j <= m; j ++){ cin >> str[i][j]; if (str[i][j] == '@') bx = i, by = j; } bfs(bx, by); cout << cnt << endl; } return 0; }
D CodeForces 1141A Game 23
Polycarp plays “Game 23”. Initially he has a number n and his goal is to transform it to mm . In one move, he can multiply n by 22 or multiply n by 33 . He can perform any number of moves.
Print the number of moves needed to transform n to mm . Print -1 if it is impossible to do so.
It is easy to prove that any way to transform n to mm contains the same number of moves
取余后判断即可
#include E POJ 1321 棋盘问题
在一个给定形状的棋盘(形状可能是不规则的)上面摆放棋子,棋子没有区别。要求摆放时任意的两个棋子不能放在棋盘中的同一行或者同一列,请编程求解对于给定形状和大小的棋盘,摆放k个棋子的所有可行的摆放方案C。
dfs入门
#includeF HDU 1087 Super Jumping!
Nowadays, a kind of chess game called “Super Jumping! Jumping! Jumping!” is very popular in HDU. Maybe you are a good boy, and know little about this game, so I introduce it to you now.
题意
- 多组输入,每行第一数字为N,其后N个数字代表N个棋盘点,大小代表该点的值
- 我们可从任意一棋盘点进行向右跳跃 但要求跳跃过程,经过点的大小逐次增大
- 输出符合条件的跳跃方案得到的最大值
上升子序列可直接暴力
- 枚举该点前所有点
- 如果
arr[i - 1] < arr[i]则可进行跳跃 - 从该点原有的值 与 新跳跃方案所得值中 取最大值
- 遍历完毕得到该点为终点得最大方案
- 最终遍历各点作为终点时的大小,选出最大值输出
#include G HDU 2161 Primes
Write a program to read in a list of integers and determine whether or not each number is prime. A number, n, is prime if its only divisors are 1 and n. For this problem, the numbers 1 and 2 are not considered primes.
判断质数
编写程序以读取整数列表,并确定每个数字是否为质数
注意输出格式,且题目中指出在该题中2不为质数
#include H CodeForces 1311B WeirdSort
You are given an array a of length n.
You are also given a set of distinct positions p_1, p_2, \dots, p_m, where 1 \le p_i < n. The position p_i means that you can swap elements a[p_i] and a[p_i + 1]. You can apply this operation any number of times for each of the given positions.
数据量很小,可直接暴力
T组数据,n个数,m个操作
每个操作 b[i]代表可将a[b[i]]与a[b[i] + 1] 进行交换
求经过交换能否数组a变为单调递增数组
#include I LightOJ 1078 Integer Divisibility
If an integer is not divisible by 2 or 5, some multiple of that number in decimal notation is a sequence of only a digit. Now you are given the number and the only allowable digit, you should report the number of digits of such multiple.
T组数据,找到N的倍数,该数只能有tim位M组成,输出M
大数取余
有一个大数989565215785528545587(大数)对10003(小数)取余,需要将该大数从最左端开始对10003取余;
start:
9%10003==9;
(9*10+8)%10003==98;
(98*10+9)%10003==989;
(989*10+5)%10003==9895;
(9895*10+6)%10003==8929;
(8929*10+5)%10003==9271;
......
取余变形
123 % 2 等价于 (3 % 2 + 20 % 2 + 100 % 2) % 2
直接暴力可过
#include J HDU 1969 Pie
My birthday is coming up and traditionally I’m serving pie. Not just one pie, no, I have a number N of them, of various tastes and of various sizes. F of my friends are coming to my party and each of them gets a piece of pie. This should be one piece of one pie, not several small pieces since that looks messy. This piece can be one whole pie though.
N种蛋糕,每个半径给出,要分给F+1个人,要求每个人分的体积一样(形状可以不一样),而且每人只能分得一种蛋糕(即一个人得到的蛋糕只能来自一块),求每人最大可以分到的体积。
double二分搜索
最小值是: 0 (大家都不吃)
最大值是:派的总体积 ÷ 总人数 (超完美平均主义)
每次取中间值 记作:mid,计算如果每个派切出 mid体积 能切多少块
如果能切够 F+1块,则将最小值更新为中间值
如果切不出 F+1块,则将最大值更新为中间值
直到两次中间值的差值 小于 10^(-4) 时就是结果了(精度)
#include K HDU 1263 水果
夏天来了好开心啊,呵呵,好多好多水果~~
Joe经营着一个不大的水果店.他认为生存之道就是经营最受顾客欢迎的水果.现在他想要一份水果销售情况的明细表,这样Joe就可以很容易掌握所有水果的销售情况了.
map
#include L CodeForces 1315A Dead Pixel
Screen resolution of Polycarp’s monitor is a×ba×b pixels. Unfortunately, there is one dead pixel at his screen. It has coordinates (x,y)(x,y) (0≤x 一个区域有一个坏点,找出正常的最大区域 即找出这个点左右上下四部分最大的一部分即可 You probably know those quizzes in Sunday magazines: given the sequence 1, 2, 3, 4, 5, what is the next number? Sometimes it is very easy to answer, sometimes it could be pretty hard. Because these “sequence problems” are very popular, ACM wants to implement them into the “Free Time” section of their new WAP portal. 差分 In mathematics, the nth harmonic number is the sum of the reciprocals of the first n natural numbers: 求f(n)=1/1+1/2+1/3+1/4…1/n (1 ≤ n ≤ 108).,精确到10-8 调和级数(即f(n))至今没有一个完全正确的公式,但欧拉给出过一个近似公式:(n很大时) 结合公式 公式: 此时公式n很大时才适用,故n很小时直接求 打表 原题n范围为1e8,每隔100个打表,即若199需要将打表所得100再执行99次,t最大为1e4,故最大为1e6,不会超时#include M HDU 1211 Complete the Sequence
n项数列的n-1阶差分,进行n-1次得到第0阶的值 类似于求导,最终差值相同且为常数(类似于求导)
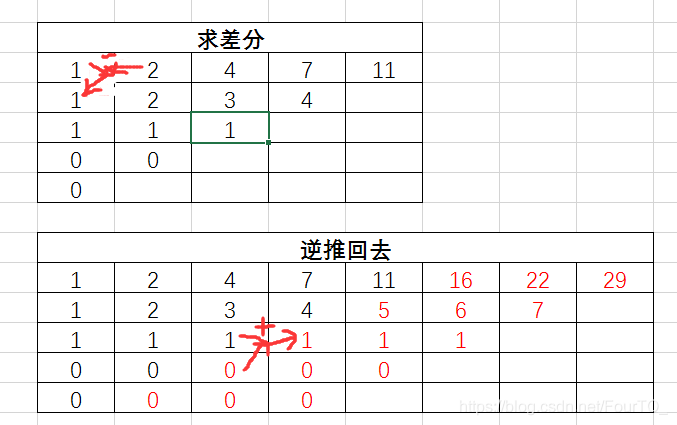
#include N LightOJ 1234 Harmonic Number
f(n)≈ln(n)+C+1/2*n欧拉常数值:C≈0.57721566490153286060651209
f(n)=ln(n)+C+1/(2*n);#include #include