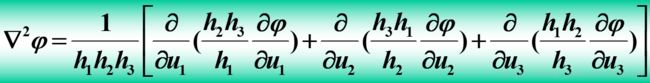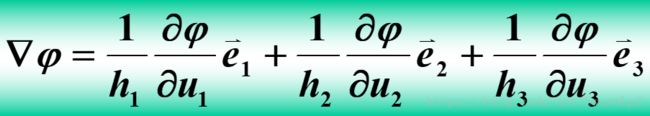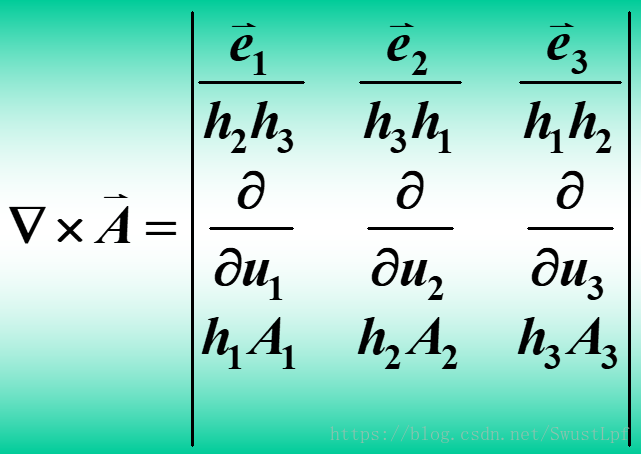拉梅系数以及雅克比行列式
文章目录
- ①直角坐标:
- ②圆柱坐标:
- ③球坐标:($\phi是2\pi那个角$)
- 然后就有一个统一的矢量场公式:
- 雅克比行列式
u 1 , u 2 , u 3 u_1,u_2,u_3 u1,u2,u3分别是不同坐标系的三个坐标, h 1 , h 2 , h 3 h_1,h_2,h_3 h1,h2,h3就是拉梅系数
①直角坐标:
u 1 = x u 2 = y u 3 = z u_1=x\ u_2=y\ u_3=z u1=x u2=y u3=z
h 1 = h 2 = h 3 = 1 h_1=h_2=h_3=1 h1=h2=h3=1
②圆柱坐标:
u 1 = ρ , u 2 = ϕ , u 3 = z u_1=\rho,u_2=\phi,u_3=z u1=ρ,u2=ϕ,u3=z
h 1 = 1 , h 2 = ρ , h 3 = 1 h_1=1,h_2=\rho,h_3=1 h1=1,h2=ρ,h3=1
③球坐标:( ϕ 是 2 π 那 个 角 \phi是2\pi那个角 ϕ是2π那个角)
u 1 = r , u 2 = θ , u 3 = ϕ u_1=r,u_2=\theta,u_3=\phi u1=r,u2=θ,u3=ϕ
h 1 = 1 , h 2 = r , h 3 = r s i n θ h_1=1,h_2=r,h_3=r sin\theta h1=1,h2=r,h3=rsinθ
然后就有一个统一的矢量场公式:
雅克比行列式
以前只在线性代数中听过这个,但是高数中也有一个
比如 d x d y = r d r d θ dxdy=rdrd\theta dxdy=rdrdθ怎么来的哇?
以前只能用画图来解释,没想到竟然有变换的公式,一直都想有,以为没有,结果真的有。。。
{ x = x ( u , v ) y = y ( u , v ) \left\{\begin{matrix} x=x(u,v)\\ \\ y=y(u,v) \end{matrix}\right. ⎩⎨⎧x=x(u,v)y=y(u,v)
J = ∣ ∂ x ∂ u ∂ x ∂ v ∂ y ∂ u ∂ y ∂ v ∣ J=\begin{vmatrix} \frac{\partial x}{\partial u}&\frac{\partial x}{\partial v}\\ \\\frac{\partial y}{\partial u} &\frac{\partial y}{\partial v} \end{vmatrix} J=∣∣∣∣∣∣∂u∂x∂u∂y∂v∂x∂v∂y∣∣∣∣∣∣
d x d y = ∣ J ∣ ⋅ d u d v dxdy=|J|\cdot dudv dxdy=∣J∣⋅dudv
有了这个公式就知道极坐标这个怎么来的了
{ x = r c o s θ y = r s i n θ \left\{\begin{matrix} x=rcos\theta\\ \\ y=rsin\theta \end{matrix}\right. ⎩⎨⎧x=rcosθy=rsinθ
J = ∣ ∂ x ∂ r ∂ x ∂ θ ∂ y ∂ r ∂ y ∂ θ ∣ = ∣ c o s θ − r s i n θ s i n θ r c o s θ ∣ = r ( c o s 2 θ + s i n 2 θ ) = r J=\begin{vmatrix} \frac{\partial x}{\partial r}&\frac{\partial x}{\partial \theta}\\ \\\frac{\partial y}{\partial r} &\frac{\partial y}{\partial \theta} \end{vmatrix}=\begin{vmatrix} cos\theta&-rsin\theta \\ & \\ sin\theta&rcos\theta \end{vmatrix}=r(cos^2\theta+sin^2\theta)=r J=∣∣∣∣∣∣∂r∂x∂r∂y∂θ∂x∂θ∂y∣∣∣∣∣∣=∣∣∣∣∣∣cosθsinθ−rsinθrcosθ∣∣∣∣∣∣=r(cos2θ+sin2θ)=r
∴ d x d y = r ⋅ d r d θ \therefore dxdy=r\cdot drd\theta ∴dxdy=r⋅drdθ