js-剑指offer刷题记录(数组)
1.二维数组中的查找
在一个二维数组中(每个一维数组的长度相同),每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
我的解法
function Find(target, array){
//从第一行开始,第一个数比target大的话,
//该行所有数都比target大,跳至下一行
for (let i=0;i<array.length;i++){
if (array[i][0]>target){
continue
}//第一个数比target小的话,该行可能有target
//用indexOf找
else{
if(array[i].indexOf(target)!=-1){
console.log('有这个数!')
return true
}
}
}
return false
}
其他分析
根据矩阵的特性,从矩阵的左下角看,往右递增往上递减,从左下角开始找,如果比target大则右移如果比target小则左移(注意分清行和列)
function Find(target,array){
var x = array.length; //行
var y = array[0].length; //列
var i = x-1;
var j = 0;
while(i>=0&&j<=y-1){
if (array[i][j]>target){
i--
}
else if(array[i][j]<target){
j++
}
else{
console.log('have')
return true
}
}
console.log('none');
return false
}
一点补充
js没有多维数组,可以通过数组包含数组创建多维数组
2.数组中重复的数字
在一个长度为n的数组里的所有数字都在0到n-1的范围内。 数组中某些数字是重复的,但不知道有几个数字是重复的。也不知道每个数字重复几次。请找出数组中任意一个重复的数字。 例如,如果输入长度为7的数组{2,3,1,0,2,5,3},那么对应的输出是第一个重复的数字2。
我的解法(弱智系列)
for循环遍历整个数组,用indexOf寻找该元素,返回的下标不是该元素的下标说明有重复元素
function duplicate(numbers, duplication){
for(let i = 0; i < numbers.length; i++){
if(numbers.indexOf(numbers[i]) != i){
duplication[0] = numbers[i]
return true
}
}
return false
}
其他分析
哈希法:用另一个长为n的数组hash,hash的下标值对应numbers中的元素值,而hash的元素值对应numbers元素出现的次数。
若numbers中元素3出现了两次,那么a[3]=2,这样遍历hash数组,哪个元素大于1则下标就是numbers中重复的元素
function duplicate1(numbers, duplication)
{
var length = numbers.length
var hash = new Array(length).fill(0)//fill方法将一个固定值替换数组的元素
for(let i=0;i<length;i++){
hash[numbers[i]]+=1
}
for(let j=0;j<length;j++){
if(hash[j]>1){
duplication[0]=j
return true
}
}
return false
}
进击:上面的做法其实把hash每个元素都赋值了,然又遍历,其实没必要,只要找到hash中第一个第一个不为0的元素就可以了
function duplicate(numbers, duplication)
{
var length = numbers.length
var hash = new Array(length).fill(0)
for(let i=0;i<length;i++){
if(hash[numbers[i]]==0){
hash[numbers[i]]+=1
}else{ //hash[numbers[i]]不为0说明重复出现了
duplication[0]=numbers[i]
return true
}
}
return false
}
数归其位:对于一个数组,把每个元素放到对应值的下标的位置上,这样对于重复的数字,一个下标就有多个数字,思想就是想办法数归其位,当发现某个元素的和值相同下标出的元素相等时,说明有重复数字(wsl)
遍历数组,判断元素a[i]和下标i是否相同
1.若相同跳过()
2.若不同,判断a[i]和a[a[i]]是否相同
2.1若不同,二者交换位置,也就是说a[i]跑到了a[i]位置 上,而a[a[i]]跑到了i位置上,对于元素a[i]来说就归位了
2.2若相同,重复元素出现了
其实元素是通过下标值这个中间量进行比较
function duplicate(numbers, duplication)
{
for(let i=0;i<numbers.length;i++){
while(i!=numbers[i]){
if(numbers[i]==numbers[numbers[i]]){
duplication[0]=numbers[i]
}else{
[numbers[i],numbers[numbers[i]]]=[numbers[numbers[i]],numbers[i]]
}
}
}
return false
}
一点补充
array.indexOf(item,start)
用于查找array中是否含有item,有则返回 item 的第一次出现的位置否则返回-1
start表示查找开始位置,没有这个参数的话则从数组开头查找
array.fill(value, start, end)
用一个固定值value填充数组,start开始位置,end终止位置,不写默认数组长度
3.构建乘积数组
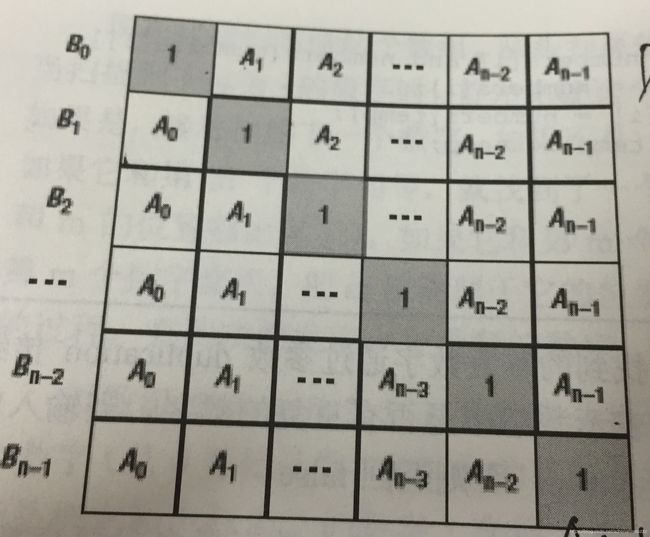
给定一个数组A[0,1,…,n-1],请构建一个数组B[0,1,…,n-1],其中B中的元素B[i]=A[0]**A[1]*…*A[i-1]A[i+1]…A[n-1]。不能使用除法。(注意:规定B[0] = A[1] * A[2] * … * A[n-1],B[n-1] = A[0] * A[1] * … * A[n-2];)
我的解法(没眼看)
根据题目可知,新数组array2的元素array2[i]等于array数组去除元素array[i]后,剩下元素的乘积。
function multiply(array)
{
var length = array.length
var array2 = []
for(let i=0;i<length;i++){
var a = array.splice(i,1) //第一步去掉array[i],返回是一个数组[array[i]]
array2[i] = array.reduce((prevalue,item)=>{
return prevalue*item
},1) //第二步reduce函数计算array剩余元素乘积
array.splice(i,0,a[0])//把去掉的array[i]塞回array,注意a是一个单个元素的数组,所以用a[0]
}
return array2
}
其他分析
其实新数组的值B[i]可看作一下数组每行的乘积,这个数组分为上下两个三角,每个三角都能连乘。先算下三角中的连乘,即先算出B[i]中的一部分,然后倒过来按上三角中的分布规律,把另一部分也乘进去。引入一个中间变量tem表示上三角连乘的结果
function multiply(array)
{
var length = array.length
var array2 = []
//下三角计算
array2[0]=1
for(let i=1;i<length;i++){
array2[i]=array2[i-1]*array[i-1]
}
//上三角计算用tem表示
let tem = 1
for(let j=length-2;j>=0;j--){
tem=tem*array[j+1]
array2[j]=array2[j]*tem
}
return array2
}
一点补充
数组方法1
array.slice(start,end)
从数组下标start处(包括start)开始选取元素,直到下标end处结束(不包括end处),选取的元素包含在返回的新数组中,但是array不改变
字符串也可以用这个方法,返回字符串
var array = [1,2,3,4,5]
var b = array.slice(2,3)
var c = array.slice(-3,-1) //slice(-3+5,-1+5)
console.log(b) //[3]
console.log(c) //[3,4]
console.log(array) //[1,2,3,4,5],不改变原数组
数组方法2
array.splice(index,howmany,item1,...,itemN)
对数组先删除后添加。从下标index处(包括index处)开始删除howmany个元素,然后把item1,…,itemN添加进去。返回包含被删除的元素的数组,原数组改变
array.splice(index,howmany)
没有item的话就是删除元素,返回包含被删除的元素的数组,当howmany为0时,表示没有删除元素,返回的数组为空
var array = [1,2,3,4,5]
var b = array.splice(2,3)
console.log(array) //[1,2],原数组改变了
console.log(b) //[3,4,5],被删元素的数组
var c = array.splice(2,0)
console.log(c) //[],没有删元素,返回空数组
console.log(array) //[1,2]
var d = array.splice(1,1,1)
console.log(d) //[2]
console.log(array); //[1,1]
4.顺时针打印矩阵
输入一个矩阵,按照从外向里以顺时针的顺序依次打印出每一个数字,例如,如果输入如下4 X 4矩阵: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 则依次打印出数字1,2,3,4,8,12,16,15,14,13,9,5,6,7,11,10.
我的解法
。。。
其他分析
打印顺序为从左到右,从上到下,从右到左,从下到上。打印的范围也随着一圈打印完而缩小。我们需要知道什么时候改变打印方向而且记录最新的打印范围。
四个变量如下
left = 0
right = matrix[0].length-1,
top = 0
bottom = matrix.length-1
循环打印:从上到下,从右到左,从下到上的顺序打印
- 根据打印边界,判断一个方向上的元素是否打印完(添加到res数组中)
- 一圈打印完,要缩小边界
- 当两边界相遇(数值相等时),打印完毕
开始我的代码这样写的
function printMatrix(matrix) //错错错
{
if(matrix == null) return null
let left = 0,
right = matrix[0].length-1,
top = 0,
bottom = matrix.length-1
let res=[]
while(left<=right&&top<=bottom){ //左右相遇且上下相遇说明没有可打印的元素了
for(let i=left;i<=right;i++){ //left > right
res.push(matrix[top][i])
}
for(let i=top+1;i<=bottom;i++){ //top > bottom
res.push(matrix[i][right])
}
for(let i=right-1;i>=left;i--){
res.push(matrix[bottom][i])
}
for(let i=bottom-1;i>top;i--){ //注意这里不能等于top,否则就会多打印矩阵右上角的元素
res.push(matrix[i][left])
}
//一圈打印完毕,缩小打印范围
left++
right--
top++
bottom--
}
return res
}
这里就出现了一个问题就是:一行/一列的矩阵,在从右往左和从上往下打印时,就会重复打印。
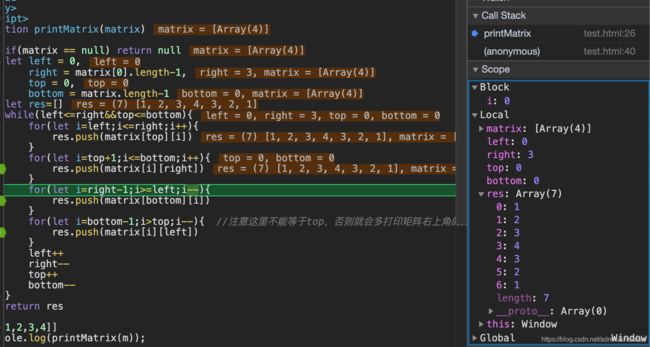
也就是说对于从右往左打印时保证top和bottom不重合,从上往下打印时保证left和right不重合。修改如下
function printMatrix(matrix)
{
if(matrix == null) return null
let left = 0,
right = matrix[0].length-1,
top = 0,
bottom = matrix.length-1
let res=[]
while(left<=right&&top<=bottom){
for(let i=left;i<=right;i++){
res.push(matrix[top][i])
}
for(let i=top+1;i<=bottom;i++){
res.push(matrix[i][right])
}
for(let i=right-1;i>=left&&top<bottom;i--){
res.push(matrix[bottom][i])
}
for(let i=bottom-1;i>top&&left<right;i--){ //注意这里不能等于top,否则就会多打印矩阵右上角的元素
res.push(matrix[i][left])
}
left++
right--
top++
bottom--
}
return res
}
5.数组中出现次数超过一半的数字
我的解法
这道题和第二题有点类似。我的思路是弄个哈希数组hash其中元素表示数组某个元素的出现次数,hash的下标值对应数组元素,从头到尾遍历数组,第一次出现就push0,否则+1。但是有个局限:数组元素不能为负。
把数组从小到大排序,重复出现的数字肯定是连着的,如果他的次数大于数组长度一半,那中位数肯定是他。
采用快速排序,或者偷懒用数组的sort()方法也可以。
function MoreThanHalfNum_Solution(numbers)
{
let hash = []
numbers.sort((a,b)=>{
return a - b
})
let mid = numbers[Math.floor(numbers.length/2)]
let count = 0
for(let item of numbers){
if(item == mid)
count++
}
return count>Math.floor(numbers.length/2)? mid:0
}
其他分析
如果存在这种数字的话,那么数组其他数字次数加起来也没有这个数字次数多。
在遍历数组时保存两个值:一是数组中一个数字,一是次数。遍历下一个数字时,若它与之前保存的数字相同,则次数加1,否则次数减1;若次数为0,则保存下一个数字,并将次数置为1。遍历结束后,所保存的数字即为所得。然后再判断它是否符合条件即可。
这是一种两两不同抵消的思想,最坏的情况,这个数字都被抵消了(如[1,2,1,2,1]),由于这个数字大于数组长度一半,他肯定还剩一个。
function MoreThanHalfNum_Solution(numbers)
{
let tmp = numbers[0]
let num = 1
for(let item of numbers){
if(item == tmp){
num++
}else{
num--
}
if(num == 0){
tmp = item
num = 1
}
}
//统计次数
let count = 0
for(let item of numbers){
if(item == tmp)
count++
}
return count>Math.floor(numbers.length/2)? tmp:0
}
6.最小的k个数
输入n个整数,找出其中最小的K个数。例如输入4,5,1,6,2,7,3,8这8个数字,则最小的4个数字是1,2,3,4。
我的解法
暴力解题
function GetLeastNumbers_Solution(input, k)
{
if(k>input.length) return []
input.sort((a,b)=>{
return a - b
})
return input.slice(0,k)
}
其他分析
看了题解多是用快排,躲不掉。其实这里利用了快排的partition函数,并没有完全对数组排序,而是找到第k小的数所在的部分,比如在右半部分,因为左半部分是比pivot小的,而k大于pivot的index,那么只要对右半部分排序就可以了,取出部分(可能左半部分不够k个数)。
function GetLeastNumbers_Solution(input, k)
{
if (input.length == 0 || k > input.length || k < 1) return []
let index = Partition(input,0,input.length-1)
//判断k的位置,这样知道在哪边找
while(index!=k-1){
if(index>k-1){
index = Partition(input,0,index-1)
}else{
index = Partition(input,index+1,input.length-1)
}
}
let res = input.slice(0,k)
res.sort((a,b)=>{return a-b}) //排序
return res
}
//partition函数很重要
function Partition(arr,left,right){
let pivot = arr[left] //比较的基准
//一直找到比基准小的数
while(left<right){
while(pivot<=arr[right]&&left<right){
right --
}
//放在前面
[arr[left],arr[right]] = [arr[right],arr[left]]
//找到比基准大的数
while(pivot>=arr[left]&&left<right){
left ++
}
//放在后面
[arr[left],arr[right]] = [arr[right],arr[left]]
//两个循环两个交换,保证左边都是比基准小的数,右边都是大的数,left为基准的下标
return left
}
}
一点补充
快排代码
function quickSort(a,left,right){
if(left==right)return;
let index=partition(a,left,right);//选出key下标
if(left<index){
quickSort(a,left,index-1);//对key的左半部分排序
}
if(index<right){
quickSort(a,index+1,right)//对key的右半部份排序
}
return a
}
function partition(a,left,right){
let pivot=a[left];//让基准为第一个数
while(left<right){
//找到比pivot小的数
while(pivot<=a[right]&&left<right){
right--;
}
//交换给前面,这样保证前面都是比基准小的数
[a[left],a[right]]=[a[right],a[left]]
//找到比pivot大的数
while(pivot>=a[left]&&left<right){
left++;
}
//交换给后面,这样后面都是比基准大的数
[a[left],a[right]]=[a[right],a[left]];//交换
}
//left和right相遇或者left超过right,返回pivot的下标
return left
}
7.连续子数组的最大和
HZ偶尔会拿些专业问题来忽悠那些非计算机专业的同学。今天测试组开完会后,他又发话了:在古老的一维模式识别中,常常需要计算连续子向量的最大和,当向量全为正数的时候,问题很好解决。但是,如果向量中包含负数,是否应该包含某个负数,并期望旁边的正数会弥补它呢?例如:{6,-3,-2,7,-15,1,2,2},连续子向量的最大和为8(从第0个开始,到第3个为止)。给一个数组,返回它的最大连续子序列的和,你会不会被他忽悠住?(子向量的长度至少是1
我的解法
反正我是被忽悠住了。
其他分析
动态规划:多用来求最值问题。
动态规划方法1
力扣上这个解析很清晰连续子数组的最大和(动态规划,清晰图解)
- 状态定义:dp[i]表示以arr[i]结尾的子数组的最大连续子数组和
- 转移方程:dp[i-1]为负,加上dp[i-1]反而会使arr[i]变小,不如取之前的arr[i];dp[i-1]为正,就要加上dp[i-1]
dp[i - 1]>0:dp[i] = dp[i-1] + arr[i]
dp[i−1]≤0 :dp[i] = arr[i] - 初始状态:dp[0] == arr[0]
function FindGreatestSumOfSubArray(array)
{
let res = array[0]
let dp = array[0]
for(let i=1;i<array.length;i++){
if(dp>0){
dp = dp+array[i]
}else{
dp = array[i]
}
res = Math.max(dp,res)
}
return res
}
动态规划方法2
- 状态定义:dp[i]表示以arr[i]结尾的子数组的最大连续子数组和
- 转移方程:dp[i] = max(dp[i-1]+array[i],array[i])
以(-2,-3,4,-1,-2)为例
dp[0] = -2
dp[1] = -3
dp[2] = 4
dp[3] = 3
… - 初始状态:dp[0] == arr[0]
function FindGreatestSumOfSubArray(array)
{
let res = array[0]
let dp = array[0]
for(let i=1;i<array.length;i++){
dp = Math.max(dp+array[i],array[i])
res = Math.max(dp,res)
}
return res
}
个人觉得第二种方法更好理解。
8.把数组排成最小的数
输入一个正整数数组,把数组里所有数字拼接起来排成一个数,打印能拼接出的所有数字中最小的一个。例如输入数组{3,32,321},则打印出这三个数字能排成的最小数字为321323。
我的解法
自暴自弃法,所有可能的组合都列出来,把最小的输出。这个真的不太现实,组合列出来的话就是之前abc字符串排列组合那道题,就真的很麻烦。
其他分析
定义新的排序规则,比较两个字符串s1, s2大小的时候,先将它们拼接起来,比较s1+s2,和s2+s1那个大,如果s1+s2大,那说明s2应该放前面,所以按这个规则,s2就应该排在s1前面。
function PrintMinNumber(numbers)
{
numbers.sort((s1,s2)=>{ //s1表示后一个数,s2表示前一个数
let a = `${s1}${s2}`
let b = `${s2}${s1}`
return a-b //return正值时,s1和s2的位置不变也就是说s1在s2的后面
})
let s = ''
for(let item of numbers){
s+=item
}
return s
}
9.数组中的逆序对
在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。 即输出P%1000000007
输入描述:
题目保证输入的数组中没有的相同的数字
数据范围:
对于%50的数据,size<=10^4
对于%75的数据,size<=10^5
对于%100的数据,size<=2*10^5
我的解法
??????
其他分析
归并算法。算法原理可以参考这片文章图解归并算法,其中这张图片很好的说明了归并算法的原理
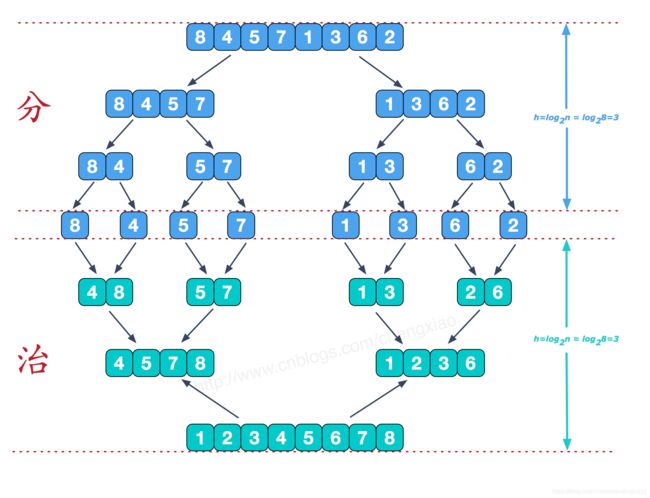
这道题就在治的过程中统计逆序对的数目。以[7,5,6,4]为例。
-
首先归并排序的分
arr分解为L= [7,5],R = [6,4];继续分解为LL = [7], LR = [5];和RL = [6], RR = [4];
自此分解完成。 -
接下来合并
i为arrLL的数组下标,j为arrLR的数组下标, index为新数组res的下标,初始值都为0- arrLL与arrLR合并
因为arrLL[i]=7 > arrLR[j]=5,所以arrLL中7及其之后的所有数字都大于arrLR中的5,也就是说7及其之后的所有元素都可以与5组成逆序对。
所以此时7及其之后的所有元素个数(leftLen - i)即我们要的逆序对数,sum += leftLen - 1
合并之后为arrL=[5,7] - 根据上述方法将arrRL和arrRR合并为arrR=[4,6]
- 将arrL和arrR合并为arr:
5 > 4,说明5及其之后的所有元素都能与4组成逆序对;所以sum += (leftLen - 1);
5 < 6,正常排序,不做处理
7 > 6,说明7及其之后的所有元素都能与6组成逆序对;所以sum += (leftLen - 1);
7,正常排序,不作处理
- arrLL与arrLR合并
function InversePairs(data)
{
var sum = 0
MergeSort(data,sum)
return sum%10000000007
//下面都是归并排序
function MergeSort(arr){
if(arr.length < 2){
return arr
}
let len = arr.length
let mid = Math.floor(len/2)
let left = arr.slice(0,mid)
let right = arr.slice(mid)
return Merge(MergeSort(left),MergeSort(right))
}
function Merge(left,right){
let res = []
let i = 0,j = 0
let leftLen = left.length
let rightLen = right.length
while(i<leftLen&&j<rightLen){
if(left[i]<right[j]){
res.push(left[i])
i++
}else{
res.push(right[j])
j++
sum += leftLen - i //与归并排序的唯一区别
}
}
while(i<leftLen){
res.push(left[i])
i++
}
while(j<rightLen){
res.push(right[j])
j++
}
return res
}
}
一点补充
归并排序代码
function MergeSort(arr){
if(arr.length < 2){ //递归出口
return arr
}
let len = arr.length
let mid = Math.floor(len/2)
//左右划分
let left = arr.slice(0,mid)
let right = arr.slice(mid)
return Merge(MergeSort(left),MergeSort(right))
}
function Merge(left,right){
let res = []
let i = 0,j = 0
let leftLen = left.length
let rightLen = right.length
while(i<leftLen&&j<rightLen){
if(left[i]<right[j]){
res.push(left[i])
i++
}else{
res.push(right[j])
j++
}
}
//可能右数组比较完了,左数组还有多的
while(i<leftLen){
res.push(left[i])
i++
}
while(j<rightLen){
res.push(right[j])
j++
}
return res
}
10.数组中出现一次的数字
一个整型数组里除了两个数字之外,其他的数字都出现了两次。请写程序找出这两个只出现一次的数字。
我的解法
用indexOf和lastIndexOf,二者返回值相等说明找到了只出现一次的数字了。一个从前往后找一个从后往前找。
function FindNumsAppearOnce(array)
{
let res = []
for(let i=0;i<array.length;i++){
if(array.indexOf(array[i])==array.lastIndexOf(array[i]))
res.push(array[i])
}
return res
}
其他分析
注意数组的特点:其他数字出现两次。异或运算有个特点:两个相同数字异或=0,一个数和0异或还是它本身。
把数组元素依次异或,最后的结果肯定就是出现一次的两个数字的异或结果,其他数字是成对的,异或都等于0了。
然后要从结果分离出两个数字:这个结果的二进制中的1,表现的是A和B的不同的位。我们就取第一个1所在的位数,假设是第3位,接着把原数组分成两组,分组标准是第3位是否为1。如此,相同的数肯定在一个组,因为相同数字所有位都相同,而不同的数,肯定不在一组。然后把这两个组按照最开始的思路,依次异或,剩余的两个结果就是这两个只出现一次的数字。
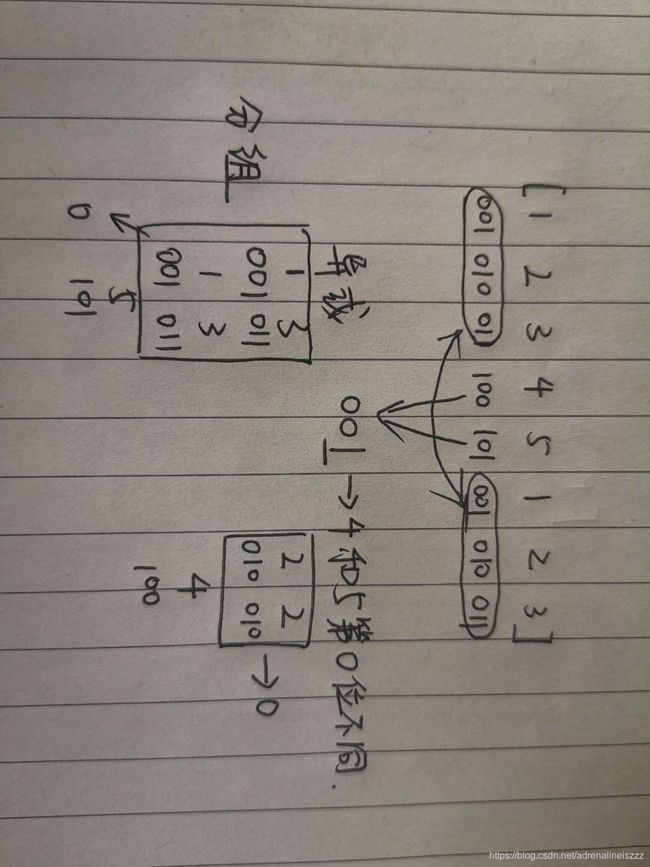
function FindNumsAppearOnce(array)
{
let tmp = array[0]
//数组异或
for(let i=1;i<array.length;i++){
tmp = tmp ^ array[i]
}
if(tmp == 0) return
//原数组分离
let index = 0
while((tmp&1) == 0){
tmp = tmp >>> 1
index ++
}
let num1=0,num2=0
for(let i=0;i<array.length;i++){
let flag = isOneOfIndex(array[i],index)
if(flag){ //flag是多少都不重要,这里就是根据index上是不是1把array中元素分开
num1 = num1^array[i]
}else{
num2 = num2^array[i]
}
}
return [num2,num1]
}
//判断num的index位上是不是1
function isOneOfIndex(num,index){
num = num>>>index
return num&1 //是1返回1就是true
}
11.数字在排序数组中出现的次数
统计一个数字在排序数组中出现的次数
我的解法
如果这个数字重复的话,由于是排序数组,肯定是连在一起。找到之后,判断下一个数是否相等,不等就返回1,相等就边计数边遍历直到与这个数不相等。
function GetNumberOfK(data, k)
{
let i=0
while(data[i]!=k){
//数字k不存在的情况
if(i==data.length){
return 0
}
i++
}
//下一个不相等或者最后一位是数字k
if(data[i+1]!==k || i==data.length-1)
return 1
let count = 0
while(data[i]==k){
count++
i++
}
return count
}
其他分析
更多采用的办法是二分查找。边界处理是真的头疼,看了好久。力扣的这篇题解中,有很直观的动画,以供参考。在排序数组中查找数字
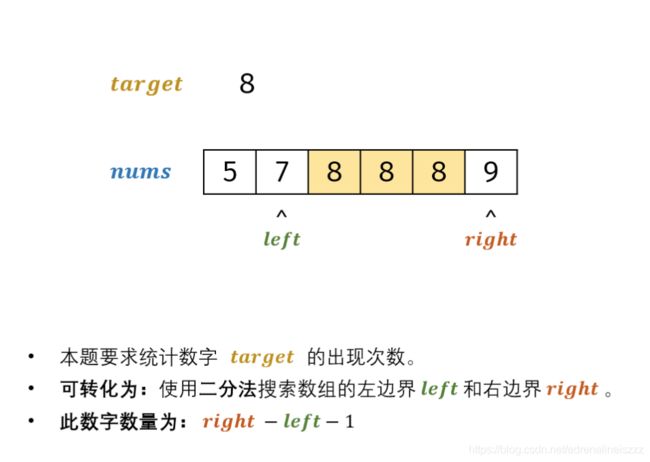
我们要通过二分法来找数组的两个边界。
- 初始化:左边界 i=0 ,右边界 j = len(data) - 1,代表闭区间 [i, j]。
- 循环二分: 和二分法一样,当i≤j时循环(即当闭区间 [i, j]为空时跳出);
计算中点 mid = (i + j)/2 ,向下取整;- 若data[mid] < k,则数字k一定在闭区间 [m + 1, j]中,因此执行 i = m + 1;
- 若data[mid] > k,则数字k一定在闭区间 [i, m - 1]中,因此执行 j = m - 1;
- 若data[mid] = k,则右边界 right在闭区间 [m+1, j]中;左边界left在闭区间[i, m-1]中。因此分为以下两种情况:
- 若查找right ,则执行 i = m + 1(跳出时i指向右边界)
- 若查找left,则执行 j = m - 1(跳出时i指向左边界)
- 返回值: 应用两次二分,分别查找right和left ,最终返回 right - left - 1即可。
function GetNumberOfK(data, k)
{
//let[i,j] = [0,data.length-1]
let i = 0
let j = data.length-1
while(i<=j){
let mid = Math.floor((i+j)/2)
if(data[mid]<k){
i = mid+1
}else{
j = mid-1
}
}
let left = j
i = 0
j = data.length-1
while(i<=j){
let mid = Math.floor((i+j)/2)
if(data[mid]<=k){
i = mid+1
}else{
j = mid-1
}
}
let right = i
return right-left-1
}
一点补充
二分查找
二分法用于有序数据的查找。
算法描述
- 选择中间值;
- 如果选择的值是待搜索的值,算法结束并返回;
- 如果待搜索值比选中值要小,则返回步骤①并在选中值左边的子数组中寻找。
- 如果待搜索值比选中值要大,则返回步骤①并在选中值右边的子数组中寻找。
其实很类似猜数字的游戏了。
function BinarySearch(arr,k){
let low = 0
let high = arr.length-1
while(low<=high){ //注意点:结束条件
let mid = Math.floor((low+high)/2) //注意点:下取整
if(arr[mid]<k) {low = mid+1}
if(arr[mid]>k) {high = mid-1}
if(arr[mid]==k) return mid
}
return low //这里return是指找不到时,k应该插入的位置
}