数据结构学习笔记(二)线性表及其C++实现
一、线性表的定义
线性表是最基本、最简单的数据结构。它是零个或多个数据元素的有限序列。由相同数据类型的n(n≥0)个元素组成的有限序列,一般表示为L=(a1, a2, ..., ai, ai+1, ..., an)。数据元素的个数n定义为表的长度。当n=0时称为空表。
它强调:
- 表中的元素个数有限;
- 表中的元素具有逻辑上的顺序性
- 集合中必存在唯一的一个“第一元素”,称为表头;
- 集合中必存在唯一的一个 “最后元素” ,称为表尾;
- 除最后一个元素之外,均有 唯一的后继;
- 除第一个元素之外,均有 唯一的前驱。
二、线性表的操作
- 计算线性表的长度;
- 判断线性表是否为空;
- 创建一个空表;
- 往线性表中添加元素;
- 删除线性表的某一个元素;
- 获取第i个元素;
- 清空线性表;
- 显示整个线性表。
三、线性表的存储结构
- 顺序存储结构:用一个数组进行描述
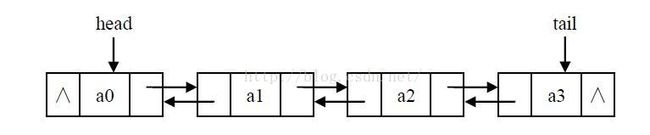
- 链式存储结构:每一个节点包含指针域和数据域,指针域指向下一个节点的地址。
除了图中的单向链表,还有双向链表,循环链表,静态链表(用数组实现指针功能)等等。
其实一般数据结构的物理存储方式也都是这两类,以后再学习和使用时要根据具体情况选择使用哪种存储方式。
四、线性表的c++语言实现
//线性表的抽象基类,函数均为纯虚函数
#pragma once
#include
using namespace std;
template
class linerList
{
public:
virtual ~linerList() {};
virtual bool empty() const = 0; //判断线性表是否为空,若为空返回true
virtual int size() const = 0; //返回线性表的元素个数
virtual T & get(int theIndex) const = 0; //返回索引为theIndex的元素
virtual int index0f(const T & theElement) const = 0; //返回元素theElement第一次出现的索引
virtual void erase(int theIndex) = 0; //删除索引为theIndex的元素
virtual void insert(int theIndex, const T & theElement) = 0; // 把theElement插入到索引为theIndex的位置上
virtual void output(ostream & out) const = 0; //输出元素
}; 线性表的顺序存储结构如下:
//类arrayList的定义和实现
#pragma once
#include
#include
#include
#include"linerList.h"
#include
#include
#include
using namespace std;
//类arrayList的定义
template
class arrayList:public linerList
{
public:
//构造函数,复制构造函数和析构函数
arrayList(int initialCapacity = 10);
arrayList(const arrayList&);
~arrayList() { delete[] element; }
//ADT方法
bool empty() const { return listSize == 0; }
int size() const { return listSize; }
T & get(int theIndex) const ;
int index0f(const T & theElement) const ;
void erase(int theIndex);
void insert(int theIndex, const T & theElement);
void output(ostream & out) const;
//其他方法
int capacity() const { return arrayLength; }//返回数组的长度,即线性表的容量
protected:
void checkIndex(int theIndex) const; //检测索引正确性,若索引无效抛出异常
T* element; // 一维数组存储线性表
int arrayLength;//一维数组的长度
int listSize;//线性表的元素个数
};
//构造函数创建一个长度为initialCapacity的数组,缺省值为10
template
arrayList::arrayList(int initialCapacity)
{
if (initialCapacity < 1)//如果initialCapacity不正确,抛出异常
{
cerr<< "Initial Capacity=" << initialCapacity << "must be>0";
exit(0);
}
arrayLength = initialCapacity;
element = new T[arrayLength];//创建数组
listSize = 0;
}
//拷贝构造函数
template
arrayList::arrayList(const arrayList& theList)
{
arrayLength = theList.arrayLength;
listSize = theList.listSize;
element = new T[arrayLength];
copy(theList.element, theList.element + listSize, element);//拷贝数组元素,利用STL中copy算法
}
//确定索引在0和listSize-1之间,
template
void arrayList::checkIndex(int theIndex) const
{
if (theIndex < 0 || theIndex >= listSize)
{
cerr<< "index:"< 0 and <= " << listSize;
exit(0);
}
}
//返回索引值为theIndex的元素,如果索引不存在抛出异常
template
T& arrayList::get(int theIndex)const
{
checkIndex(theIndex);
return element[theIndex];
}
//返回theElement第一次出现时的索引,如果元素不存在返回-1
template < class T>
int arrayList::index0f(const T& theElement) const
{
int theIndex = (int)(find(element, element + listSize, theElement) - element);//先查找,利用STl中的find算法
if (theIndex == listSize)
return -1;
else
return theIndex;
}
// 删除索引theIndex的元素
template
void arrayList::erase(int theIndex)
{
checkIndex(theIndex);
copy(element + theIndex + 1, element + listSize, element + theIndex);//索引有效的情况下。移动大于索引的元素
element[--listSize].~T();//调用析构函数
}
//插入操作
template
void arrayList::insert(int theIndex, const T& theElement)
{
if (theIndex<0 || theIndex>listSize)//无效索引抛出异常
{
cerr << "index:" << theIndex << " must be > 0 and <= " << listSize;
exit(0);
}
if (listSize == arrayLength)//数组已满,扩充数组
{
addLength1D(element, arrayLength, 2 * arrayLength);
arrayLength *= 2;
}
copy_backward(element + theIndex, element + listSize, element + listSize + 1);//将元素右移一个位置
element[theIndex] = theElement;
listSize++;
}
//输出,为什么要这样,有什么优点呢?
template
void arrayList::output(ostream& out)const //把线性表插入输入输出流
{
copy(element, element + listSize, ostream_iterator(out, " "));
}
template
ostream& operator<<(ostream & out, const arrayList& x)//函数重载
{
x.output(out);
return out;
}
//当数组长度不够时,通过该函数扩展存储空间
template
void addLength1D(T*& a, int oldLength, int newLength)
{
if (newLength < 0)
cerr<<"new length must be >=0";
T *temp = new T[newLength]; //新数组
int number = min(oldLength, newLength); //需要复制的元素个数
copy(a, a + number, temp); //复制元素
delete[] a; //释放旧的元素内存空间
a = temp;
} 测试代码:
#include"arrayList.h"
#include
using namespace std;
void main()
{
//arrayList listwrong(0); 错误,抛出异常
arrayList list(10);
cout << list.capacity();
cout << endl;
list.insert(0, 0);
list.insert(1, 1);
list.insert(2, 2);
list.insert(3, 3);
list.insert(4, 4);
list.insert(5, 5);
list.insert(6, 6);
list.insert(7, 7);
cout << list;
cout << endl;
list.insert(4, 100);
cout << list;
cout << endl;
list.erase(2);
cout << list;
cout << endl;
cout< 线性表的链式存储结构如下:
//类chain的定义和实现
#pragma once
#include
#include
#include
#include"linerList.h"
#include
#include
#include
using namespace std;
//链表节点的结构表示
template
struct chainNode
{
T element;//数据域
chainNode *next;//指针域
chainNode() {}//默认构造函数
chainNode(const T& element) { this->element = element; }//构造函数
chainNode(const T& element, chainNode* next)
{
this->element = element;
this->next = next;
}
};
template
class chain :public linerList
{
public:
//构造函数,复制构造函数和析构函数
chain(int initialCapacity=10);
chain(const chain&);
~chain();
//抽象数据类型的ADT方法
bool empty() const { return listSize == 0; }; //判断线性表是否为空,若为空返回true
int size() const { return listSize; }; //返回线性表的元素个数
T & get(int theIndex) const ; //返回索引为theIndex的元素
int index0f(const T& theElement) const; //返回元素theElement第一次出现的索引
void erase(int theIndex); //删除索引为theIndex的元素
void insert(int theIndex, const T & theElement); // 把theElement插入到索引为theIndex的位置上
void output(ostream& out) const ; //输出元素
//其他方法
void clear();//清空表
protected:
void checkIndex(int theIndex) const;//如果索引无效,抛出异常
chainNode* firstNode;//指向链表的第一个节点的指针
int listSize;//线性表中元素个数
};
//构造函数,创建一个空的链表,这里的预定义容量不是必须的,只是为了与arrayList兼容
template
chain::chain(int initialCapacity)
{
if (initialCapacity < 1)
{
cerr << "Initial Capacity=" << initialCapacity << "must be>0";
exit(0);
}
firstNode = NULL;
listSize = 0;
}
//复制构造函数
template
chain::chain(const chain& theList)
{
listSize = theList.listSize;
//链表为空时
if (listSize==0)
{
firstNode = NULL;
return;
}
//链表非空时
chainNode* sourceNode = theList.firstNode;
firstNode = new chainNode(sourceNode->element);//复制链表theList的首元素
sourceNode = sourceNode->next;
chainNode* targetNode = firstNode;
while (sourceNode!=NULL)
{
targetNode->next = new chainNode(sourceNode->element);
targetNode = targetNode->next;
sourceNode = sourceNode->next;
}
targetNode->next = NULL;
}
//析构函数,删除所有节点,最后firstNode为NULL
template
chain::~chain()
{
while (firstNode != NULL)
{
chainNode * nextNode = firstNode->next;
delete firstNode;
firstNode = nextNode;
}
}
//找到索引为theIndex的元素
template
T& chain::get(int theIndex) const
{
checkIndex(theIndex);
chainNode* currentNode = firstNode;//使用currentNode作为指示器寻找元素
for (int i = 0; i < theIndex; i++)
currentNode = currentNode->next;
return currentNode->element;
}
//返回元素theElement首次出现的索引,没找到返回-1
template
int chain::index0f(const T& theElement) const
{
chainNode* currentNode = firstNode;//使用currentNode作为指示器
int index = 0;
while (currentNode != NULL && currentNode->element != theElement)
{
currentNode = currentNode->next;
index++;
}
if (currentNode == NULL)//确定是否找到并返回
return -1;
else
return index;
}
//删除索引为theIndex的元素
template
void chain::erase(int theIndex)
{
checkIndex(theIndex);//索引无效的情况
//索引有效
chainNode * deleteNode;
if (theIndex == 0)//如果在首位置,删除首节点
{
deleteNode = firstNode;
firstNode = firstNode->next;
}
else//找到位置后删除节点,p指向删除节点的前驱
{
chainNode* p = firstNode;
for (int i = 0; i < theIndex; i++)
p = p->next;
deleteNode = p->next;
p->next = p->next->next;//删除指针
}
listSize--;
delete deleteNode;
}
//插入元素theElement并使其索引为theIndex
template
void chain::insert(int theIndex, const T& theElement)
{
if (theIndex<0 || theIndex>listSize)
{
cerr << "index:" << theIndex << " must be > 0 and <= " << listSize;
exit(0);
}
if (theIndex == 0)//在表头插入
{
firstNode = new chainNode(theElement, firstNode);
}
else//先找到位置,p为指示器在p后面插入
{
chainNode* p = firstNode;
for (int i = 0; i < theIndex - 1; i++)
p = p->next;
p->next = new chainNode(theElement, p->next);//在p后插入
}
listSize++;
}
//输出链表
template
void chain::output(ostream &out)const
{
for (chainNode* currentNode = firstNode; currentNode != NULL; currentNode = currentNode->next)
out << currentNode->element << " ";
}
template
ostream & operator<<(ostream & out, const chain& x)
{
x.output(out);
return out;
}
//确定索引在0和listSize-1之间,
template
void chain::checkIndex(int theIndex) const
{
if (theIndex < 0 || theIndex >= listSize)
{
cerr << "index:" << theIndex << " must be > 0 and <= " << listSize;
exit(0);
}
}
//清表
template
void chain::clear()
{
while (firstNode != NULL)
{
chainNode* nextNode = firstNode->next;
delete firstNode;
firstNode = nextNode;
}
listSize = 0;
} 测试代码:
#include"chain.h"
#include
using namespace std;
void main()
{
chain list(10);
for (int i = 0; i < 9; i++)
list.insert(i,i);
cout << list << endl;
list.insert(4, 100);
cout << list;
cout << endl;
list.erase(2);
cout << list << endl;
cout<