优化器算法总结（BGD、SGD、MBGD、Momentum、NAG、Adagrad 未总结完）

参考的两篇博文

(1) 优化算法总结-深度学习  https://blog.csdn.net/fengzhongluoleidehua/article/details/81104051 

(2) 深度学习——优化器算法Optimizer详解（BGD、SGD、MBGD、Momentum、NAG、Adagrad、Adadelta、RMSprop、Adam） https://www.cnblogs.com/guoyaohua/p/8542554.html （看这篇就好）

https://www.jianshu.com/p/aebcaf8af76e (Adam)

---

1.Batch Gradient Descent （BGD）

梯度更新规则:

BGD 采用整个训练集的数据来计算 cost function 对参数的梯度：

 

for i in range(nb_epochs):
  params_grad = evaluate_gradient(loss_function, data, params)
  params = params - learning_rate * params_grad

我们会事先定义一个迭代次数 epoch，首先计算梯度向量 params_grad，然后沿着梯度的方向更新参数 params，learning rate 决定了我们每一步迈多大。

缺点： 
由于这种方法是在一次更新中，就对整个数据集计算梯度，所以计算起来非常慢，遇到很大量的数据集也会非常棘手，而且不能投入新数据实时更新模型。 
优点：
Batch gradient descent 对于凸函数可以收敛到全局极小值，对于非凸函数可以收敛到局部极小值。

2.Stochastic Gradient Descent (SGD)

for i in range(nb_epochs):
  np.random.shuffle(data)
  for example in data:
    params_grad = evaluate_gradient(loss_function, example, params)
    params = params - learning_rate * params_grad

优点：和 BGD 的一次用所有数据计算梯度相比，SGD 每次更新时对每个样本进行梯度更新，对于很大的数据集来说，可能会有相似的样本，这样 BGD 在计算梯度时会出现冗余，而 SGD 一次只进行一次更新，就没有冗余，而且比较快，并且可以新增样本。虽然包含一定的随机性，但是从期望上来看，它是等于正确的导数的。 
缺点： 
SGD 因为更新比较频繁，会造成 cost function 有严重的震荡。 
BGD 可以收敛到局部极小值，当然 SGD 的震荡可能会跳到更好的局部极小值处。当我们稍微减小 learning rate，SGD 和 BGD 的收敛性是一样的。

3.Mini-Batch Gradient Descent （MBGD）

梯度更新规则： 
MBGD 每一次利用一小批样本，即 n 个样本进行计算，这样它可以降低参数更新时的方差，收敛更稳定，另一方面可以充分地利用深度学习库中高度优化的矩阵操作来进行更有效的梯度计算。和 SGD 的区别是每一次循环不是作用于每个样本，而是具有 n 个样本的批次。

缺点：（两大缺点）

1.不过 Mini-batch gradient descent 不能保证很好的收敛性，learning rate 如果选择的太小，收敛速度会很慢，如果太大，loss function 就会在极小值处不停地震荡甚至偏离。（有一种措施是先设定大一点的学习率，当两次迭代之间的变化低于某个阈值后，就减小 learning rate，不过这个阈值的设定需要提前写好，这样的话就不能够适应数据集的特点。）对于非凸函数，还要避免陷于局部极小值处，或者鞍点处，因为鞍点周围的error是一样的，所有维度的梯度都接近于0，SGD 很容易被困在这里。（会在鞍点或者局部最小点震荡跳动，因为在此点处，如果是训练集全集带入即BGD，则优化会停止不动（why?），如果是mini-batch或者SGD，每次找到的梯度都是不同的，就会发生震荡，来回跳动。） 
2.SGD对所有参数更新时应用同样的 learning rate，如果我们的数据是稀疏的，我们更希望对出现频率低的特征进行大一点的更新。Lr会随着更新的次数逐渐变小。

4.Momentum

SGD 在 ravines 的情况下容易被困住， ravines 就是曲面的一个方向比另一个方向更陡，这时 SGD 会发生震荡而迟迟不能接近极小值：

梯度更新规则: 
Momentum 通过加入 γv_t−1 ，可以加速 SGD， 并且抑制震荡 

当我们将一个小球从山上滚下来时，没有阻力的话，它的动量会越来越大，但是如果遇到了阻力，速度就会变小。
加入的这一项，可以使得梯度方向不变的维度上速度变快，梯度方向有所改变的维度上的更新速度变慢，这样就可以加快收敛并减小震荡。

超参数设定值:  一般 γ 取值 0.9 左右。

★在下降初期，使用前一次的大比重下降方向，加速。

★在越过函数谷面时，异常的学习率，会使得两次更新方向基本相反，在原地”震荡“. 此时，动量因子使得更新幅度减小，协助越过函数谷面。

★在下降中后期，函数面局部最小值所在的吸引盆数量较多，一旦陷进吸引盆当中，Gradient→0，但是前后两次更新方向基本相同。 
此时，动量因子使得更新幅度增大，协助跃出吸引盆。 

优点 

★可以使得梯度方向不变的维度上速度变快，梯度方向有所改变的维度上的更新速度变慢，这样就可以加快收敛并减小震荡。 

缺点 

★这种情况相当于小球从山上滚下来时是在盲目地沿着坡滚，如果它能具备一些先知，例如快要上坡时，就知道需要减速了的话，适应性会更好。

5.Nesterov Accelerated Gradient

梯度更新规则: 
用 θ−γv_t−1 来近似当做参数下一步会变成的值，则在计算梯度时，不是在当前位置，而是未来的位置上 

 
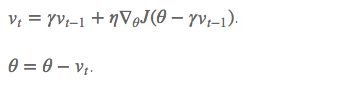
超参数设定值: 一般 γ 仍取值 0.9 左右。 
效果比较：

 
蓝色是 Momentum 的过程，会先计算当前的梯度，然后在更新后的累积梯度后会有一个大的跳跃。 
而 NAG 会先在前一步的累积梯度上(brown vector)有一个大的跳跃，然后衡量一下梯度做一下修正(red vector)，这种预期的更新可以避免我们走的太快。 
NAG 可以使 RNN 在很多任务上有更好的表现。 
目前为止，我们可以做到，在更新梯度时顺应 loss function 的梯度来调整速度，并且对 SGD 进行加速。我们还希望可以根据参数的重要性而对不同的参数进行不同程度的更新。

6.Adagrad （Adaptive gradient algorithm）
这个算法就可以对低频的参数做较大的更新，对高频的做较小的更新，也因此，对于稀疏的数据它的表现很好，很好地提高了 SGD 的鲁棒性，例如识别 Youtube 视频里面的猫，训练 GloVe word embeddings，因为它们都是需要在低频的特征上有更大的更新。

梯度更新规则: 
 
其中 g 为：t 时刻参数 θ_i 的梯度 
 
如果是普通的 SGD， 那么 θ_i 在每一时刻的梯度更新公式为： 
 
但这里的 learning rate η 也随 t 和 i 而变： 
 
超参数设定值：一般η选取0.01 
优点： 
Adagrad 的优点是减少了学习率的手动调节

缺点： 
它的缺点是分母会不断积累，这样学习率就会收缩并最终会变得非常小。其中 G_t 是个对角矩阵， (i,i) 元素就是 t 时刻参数 θ_i 的梯度平方和。 
超参数设定值：一般η选取0.01

7.Adadelta
AdaDelta的缺陷

超参数设定值: γ 一般设定为 0.9

局部最小值 
从多个数据集情况来看，AdaDelta在训练初期和中期，具有非常不错的加速效果。但是到训练后期，进入局部最小值雷区之后，AdaDelta就会反复在局部最小值附近抖动。 
主要体现在验证集错误率上，脱离不了局部最小值吸引盆。这时候，切换成动量SGD，如果把学习率降低一个量级，就会发现验证集正确率有2%~5%的提升，这与常规使用动量SGD，是一样的。之后再切换成AdaDelta，发现正确率又退回去了。再切换成动量SGD，发现正确率又回来了。

注：使用Batch Norm之后，这样从AdaDelta切到SGD会导致数值体系崩溃，原因未知。 
个人猜测，人工学习率的量级降低，给训练造成一个巨大的抖动，从一个局部最小值，抖动到了另一个局部最小值，而AdaDelta的二阶近似计算，或者说所有二阶方法，则不会产生这么大的抖动，所以很难从局部最小值中抖出来。这给追求state of art的结果带来灾难，因为只要你一直用AdaDelta，肯定是与state of art无缘的。基本上state of art的结果，最后都是SGD垂死挣扎抖出来的。 
这也是SGD为什么至今在state of art的论文中没有废除的原因，人家丑，但是实在。 
精度 
eps的数值不是固定的。1e-6在Caffe Cifar10上就显得过小了，1e-8比较适合。这意味着不同数值比例体系，精度需要人工注意。 
paper里高精度反而没低精度好，说明精度也有比较大抖动。so，究竟什么样的精度是最好的呢？

在FCNN-AlexNet里，1e-8在epoch1之后就会产生数值问题。原因是sqrt(1e-8)*grad很大，这时候1e-10是比较好的。 
另外，DensePrediction一定要做normalize，否则也有可能让AdaDelta的迭代步长计算出现数值问题。该问题在FCNN-AlexNet进行到epoch5左右时候开始明显化。caffe默认给的1e-10实际上要比paper里的1e-6要相对robust。

8.RMSprop
超参数设定值:

Hinton 建议设定 *γ 为 0.9, 学习率 η 为 0.001*

RMSprop 是 Geoff Hinton 提出的一种自适应学习率方法。 
RMSprop 和 Adadelta 都是为了解决 Adagrad 学习率急剧下降问题的， 
梯度更新规则: 
 
RMSprop 与 Adadelta 的第一种形式相同：（使用的是指数加权平均，旨在消除梯度下降中的摆动，与Momentum的效果一样，某一维度的导数比较大，则指数加权平均就大，某一维度的导数比较小，则其指数加权平均就小，这样就保证了各维度导数都在一个量级，进而减少了摆动。允许使用一个更大的学习率η）

RMSprop 与 Adadelta 的第一种形式相同：（使用的是指数加权平均，旨在消除梯度下降中的摆动，与Momentum的效果一样，某一维度的导数比较大，则指数加权平均就大，某一维度的导数比较小，则其指数加权平均就小，这样就保证了各维度导数都在一个量级，进而减少了摆动。允许使用一个更大的学习率η）

9.Adam：Adaptive Moment Estimation
超参数设定值: 
建议* β1 ＝ 0.9，β2 ＝ 0.999，ϵ ＝ 10e−8*

这个算法是另一种计算每个参数的自适应学习率的方法。相当于 RMSprop + Momentum 
除了像 Adadelta 和 RMSprop 一样存储了过去梯度的平方 vt 的指数衰减平均值 ，也像 momentum 一样保持了过去梯度 mt 的指数衰减平均值： 
如果 mt 和 vt 被初始化为 0 向量，那它们就会向 0 偏置，所以做了偏差校正，通过计算偏差校正后的 mt 和 vt 来抵消这些偏差： 
 
如果 mt 和 vt 被初始化为 0 向量，那它们就会向 0 偏置，所以做了偏差校正，通过计算偏差校正后的 mt 和 vt 来抵消这些偏差： 
 
梯度更新规则: 
 
实践表明，Adam 比其他适应性学习方法效果要好

二.效果比较

上面两种情况都可以看出，Adagrad, Adadelta, RMSprop 几乎很快就找到了正确的方向并前进，收敛速度也相当快，而其它方法要么很慢，要么走了很多弯路才找到。

由图可知自适应学习率方法即 Adagrad, Adadelta, RMSprop, Adam 在这种情景下会更合适而且收敛性更好。

三.如何选择优化算法
如果数据是稀疏的，就用自适用方法，即 Adagrad, Adadelta, RMSprop, Adam。

RMSprop, Adadelta, Adam 在很多情况下的效果是相似的。

Adam 就是在 RMSprop 的基础上加了 bias-correction 和 momentum，随着梯度变的稀疏，Adam 比 RMSprop 效果会好。

整体来讲，Adam 是最好的选择。

很多论文里都会用 SGD，没有 momentum 等。SGD 虽然能达到极小值，但是比其它算法用的时间长，而且可能会被困在鞍点。

如果需要更快的收敛，或者是训练更深更复杂的神经网络，需要用一种自适应的算法。
--------------------- 
作者：SoftGit 
来源：CSDN 
原文：https://blog.csdn.net/fengzhongluoleidehua/article/details/81104051 
版权声明：本文为博主原创文章，转载请附上博文链接！