前端工程师的 LeetCode 之旅 -- 周赛 200
01
统计好三元组
题目描述【Easy】
给你一个整数数组 arr ,以及 a、b 、c 三个整数。请你统计其中好三元组的数量。
如果三元组 (arr[i], arr[j], arr[k]) 满足下列全部条件,则认为它是一个 好三元组 。
0 <= i < j < k < arr.length
|arr[i] - arr[j]| <= a
|arr[j] - arr[k]| <= b
|arr[i] - arr[k]| <= c
其中 |x| 表示 x 的绝对值。
返回 好三元组的数量
输入:arr = [3,0,1,1,9,7], a = 7, b = 2, c = 3
输出:4
解释:一共有 4 个好三元组:[(3,0,1), (3,0,1), (3,1,1), (0,1,1)] 。
本道题主要考察数组的遍历,需要特别注意三个数字的下标是不能相同的。
时间复杂度 O(n^3),空间复杂度 O(1)。
const countGoodTriplets = function(arr, a, b, c) {
const max = arr.length;
let ans = 0;
for (let i = 0; i < max - 2; i++) {
for (let j = i + 1; j < max - 1; j++) {
for (let k = j + 1; k < max; k++) {
if (Math.abs(arr[i] - arr[j]) <= a && Math.abs(arr[j] - arr[k]) <= b && Math.abs(arr[i] -arr[k]) <= c) {
ans++;
}
}
}
}
return ans;
};
02
找出数组游戏的赢家
题目描述【Medium】
给你一个由 不同 整数组成的整数数组 arr 和一个整数 k 。
每回合游戏都在数组的前两个元素(即 arr[0] 和 arr[1] )之间进行。比较 arr[0] 与 arr[1] 的大小,较大的整数将会取得这一回合的胜利并保留在位置 0 ,较小的整数移至数组的末尾。当一个整数赢得 k 个连续回合时,游戏结束,该整数就是比赛的 赢家 。
返回赢得比赛的整数。
题目数据 保证 游戏存在赢家。
示例:
输入:arr = [3,2,1], k = 10
输出:3
解释:3 将会在前 10 个回合中连续获胜。
题目非常容易理解,在数组迭代的过程中,不断比较前两个数的大小,并且记录较大数的获胜回合数,当获胜回合数等于 k 时,返回较大的数。
需要注意的一点就是:当 k 大于数组长度时,能够赢得这么多回合的数只能是当前数组的最大值。
这样可以将时间复杂度优化为 O(min(arr.length, k) * arr.length)。
const getWinner = function(arr, k) {
const len = arr.length;
let max = Number.MIN_SAFE_INTEGER;
let count = 0;
let temp = 0;
while (count < k) {
const first = arr[0];
const next = arr[1] || Number.MIN_SAFE_INTEGER;
if (first > next) {
count++;
arr.splice(1, 1);
arr.push(next);
} else {
count = 1;
arr.splice(0, 1);
arr.push(first);
}
max = Math.max(first, next);
temp++;
if (temp >= len) {
return max;
}
}
return arr[0];
};
上述解法中利用 splice 和 push 方法进行数组元素的交换,从而达到更新前两位数的目的。
但是这里其实没有必要更新前两位数,因为一次遍历就能知道结果,所以只要记录当前两个数的下标即可。
利用双指针记录当前两个数的下标,即可优化掉 splice 带来的时间复杂度,从而整体时间复杂度优化为 O(n)。
const getWinner = function(arr, k) {
let preIndex = 0;
let nextIndex = 1;
let count = 0;
let maxNum = Number.MIN_SAFE_INTEGER;
while (nextIndex < arr.length) {
if (arr[nextIndex] < arr[preIndex]) {
count++;
} else {
count = 1;
preIndex = nextIndex;
}
if (count === k) {
return arr[preIndex];
}
maxNum = Math.max(maxNum, arr[nextIndex], arr[preIndex]);
nextIndex++;
}
return maxNum;
};
03
排布二进制网格的最少交换次数
题目描述【Medium】
给你一个 n x n 的二进制网格 grid,每一次操作中,你可以选择网格的 相邻两行 进行交换。
一个符合要求的网格需要满足主对角线以上的格子全部都是 0 。
请你返回使网格满足要求的最少操作次数,如果无法使网格符合要求,请你返回 -1 。
主对角线指的是从 (1, 1) 到 (n, n) 的这些格子。
示例:
输入:grid = [[0,0,1],[1,1,0],[1,0,0]]
输出: 3
本道题的难点在于理解题意,明白依据什么进行相邻两行的交换?
最终是要完成主对角线右上方全是零,那么交换的目的就是将右边连续 0 最多的行移动到最高层。
首先需要记录每一行右边连续 0 的个数,然后根据连续 0 个数与行数的关系进行交换操作。
时间复杂度 O(n^3)。
const minSwaps = function(grid) {
const row = grid[0].length;
// 统计每一行右边连续 0 的个数
const record = Array(row).fill(0);
for (let i = 0; i < row; i++) {
for (let j = row - 1; j >= 0; j--) {
if (grid[i][j] == 0) {
record[i]++;
} else {
break;
}
}
}
let step = 0;
for (let i = 0; i < row - 1; i++) {
const currentMinZero = row - 1 - i;
if (record[i] >= currentMinZero) {
continue;
}
let isFlag = true; // 不可以将右上角全部填充成 0
for (let j = i + 1; j < row; j++) {
if (record[j] >= currentMinZero) {
step += (j - i);
const temp = record[j];
record.splice(j, 1);
record.splice(i, 0, temp);
isFlag = false;
break;
}
}
if (isFlag) {
return -1;
}
}
return step;
};
04
最大得分
题目描述【Hard】
你有两个 有序 且数组内元素互不相同的数组 nums1 和 nums2 。
一条 合法路径 定义如下:
选择数组 nums1 或者 nums2 开始遍历(从下标 0 处开始)。
从左到右遍历当前数组。
如果你遇到了 nums1 和 nums2 中都存在的值,那么你可以切换路径到另一个数组对应数字处继续遍历(但在合法路径中重复数字只会被统计一次)。
得分定义为合法路径中不同数字的和。
请你返回所有可能合法路径中的最大得分。
由于答案可能很大,请你将它对 10^9 + 7 取余后返回。
示例:
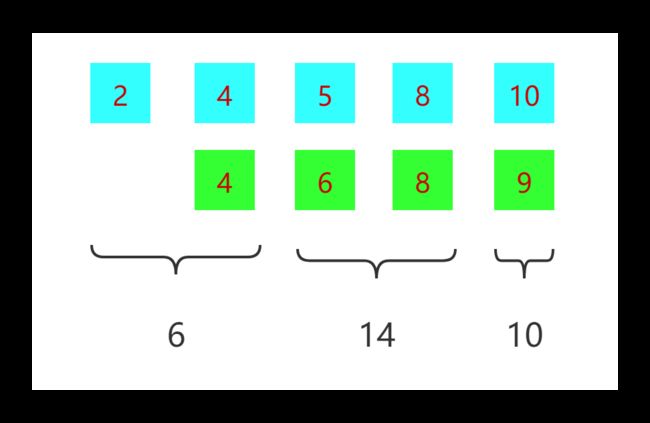
输入:nums1 = [2,4,5,8,10], nums2 = [4,6,8,9]
输出:30
解释:合法路径包括:
[2,4,5,8,10], [2,4,5,8,9], [2,4,6,8,9], [2,4,6,8,10],(从 nums1 开始遍历)
[4,6,8,9], [4,5,8,10], [4,5,8,9], [4,6,8,10] (从 nums2 开始遍历)
最大得分为上图中的绿色路径 [2,4,6,8,10] 。
不要把本道题想得太复杂,保持局部路径得分最大,那么最终的合法路径的得分就最大。
利用双指针遍历两个数组,同时记录两个分支的得分,当遇到相同节点时,取分支中最大的得分,并且重新开始计分,最终各分支的最大得分和即为结果。
时间复杂度 O(n)。
const maxSum = function(nums1, nums2) {
let sum1 = 0;
let sum2 = 0;
let maxSum = 0;
let startNums1Index = 0;
let startNums2Index = 0;
while (startNums1Index < nums1.length && startNums2Index < nums2.length) {
if (nums1[startNums1Index] === nums2[startNums2Index]) {
maxSum += (Math.max(sum1, sum2) + nums1[startNums1Index]);
sum1 = 0;
sum2 = 0;
startNums1Index++;
startNums2Index++;
} else if (nums1[startNums1Index] < nums2[startNums2Index]) {
sum1 += nums1[startNums1Index];
startNums1Index++;
} else {
sum2 += nums2[startNums2Index];
startNums2Index++;
}
}
while(startNums1Index < nums1.length) {
sum1 += nums1[startNums1Index];
startNums1Index++;
}
while(startNums2Index < nums2.length) {
sum2 += nums2[startNums2Index];
startNums2Index++;
}
maxSum += Math.max(sum1, sum2);
return maxSum % (10 ** 9 + 7);
};
05
往期精彩回顾
前端工程师的 LeetCode 之旅 -- 周赛 185
前端工程师的 LeetCode 之旅 -- 周赛 184
前端工程师的 LeetCode 之旅 -- 周赛 183
前端工程师的 LeetCode 之旅 -- 周赛 182
![]()
你点的每个赞,我都认真当成了喜欢