CS224n学习笔记 01_Introduction and Word Vectors
CS224n学习笔记 01
- How do we represent the meaning of a word?
- How do we have usable meaning in a computer?
- 1. WordNet
- 2. One-Hot: Representing words as discrete symbols
- 3. Word Vector: Representing words by their context
- 4. Word2vec
人类之所以比类人猿更“聪明”,是因为我们有语言,因此是一个人机网络,其中人类语言作为网络语言。人类语言具有 信息功能 和 社会功能 。据估计,人类语言只有大约5000年的短暂历。语言是人类变得强大的主要原因。写作是另一件让人类变得强大的事情。它是使知识能够在空间上传送到世界各地,并在时间上传送的一种工具。但是,相较于如今的互联网的传播速度而言,人类语言是一种缓慢的语言。然而,只需人类语言形式的几百位信息,就可以构建整个视觉场景。这就是自然语言如此迷人的原因。
NLP(Natural Language Processing),就是利用计算机处理自然语言文本的技术。
How do we represent the meaning of a word?
自然语言的意义,包括:
- 用一个词、词组等表示的概念;
- 一个人想用语言、符号等来表达的想法;
- 表达在作品、艺术等方面的思想。
理解自然语言的意义最普遍的语言方式(linguistic way) : 语言符号与语言符号的意义的转化
signifier(symbol) ⇔ signified(idea or thing) = denotational semantics \boxed{\text{signifier(symbol)}\Leftrightarrow \text{signified(idea or thing)}} \ = \textbf{denotational semantics} signifier(symbol)⇔signified(idea or thing) =denotational semantics
How do we have usable meaning in a computer?
1. WordNet
WordNet是一个包含同义词集和上位词(“is a”关系) synonym sets and hypernyms 的列表的辞典,使用样例如下图:

WordNet存在的问题:
- 是很好的资源但忽略了细微的一些差别:例如词典中‘proficient’与‘good’认为是同义词,但是这只在某些文本上下文中成立。
- 忽略了一些单词的含义(即含义不完整);
- 偏主观(缺少客观性);
- 需要人类来不断地更新和改写;
- 无法计算单词之间的相似度。
2. One-Hot: Representing words as discrete symbols
在传统的自然语言处理中,我们把词语看作离散的符号: hotel, conference, motel - a localist representation。单词可以通过独热向量(one-hot vectors,只有一个1,其余均为0的稀疏向量) 。向量维度=词汇量(如500,000)。
m o t e l = [ 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 ] h o t e l = [ 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 ] motel = [0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 1 \ 0 \ 0 \ 0 \ 0] \\ hotel = [0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 1 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0] motel=[0 0 0 0 0 0 0 0 0 0 1 0 0 0 0]hotel=[0 0 0 0 0 0 0 1 0 0 0 0 0 0 0]
one-hot编码存在的问题:
- 由于所有的one-hot vectors都是正交的,因此没有办法计算向量之间相似度;
- 当词汇量大时,向量维度容易过大。
3. Word Vector: Representing words by their context
这种方式的思想的核心在于——Distributional semantics(一个单词的意思是由经常出现在它附近的单词给出的)。
因此,我们可以利用词w的多个上下文词,去建立一个词w的表示。 例如在下图中,可以利用banking的上下文词来建立一个banking的表示:

基于Distributional semantics的思想,我们提出了词向量word vectors,它是我们为每个单词构建一个密集的向量,使其与出现在相似上下文中的单词向量相似,有时又被称为词嵌入 word embeddings或词表示word representations。例如banking的词向量:

4. Word2vec
**Word2vec (Mikolov et al. 2013)**是一个利用文件文本语料训练词向量的框架,它的思想包括以下几点:
- 我们有大量的文本 (corpus means ‘body’ in Latin. 复数为corpora);
- 固定文本词汇表中的每个单词都由一个向量表示;
- 文本中的每个位置t,其中有一个中心词c和上下文(“外部”)单词o;
- 使用c和o的词向量的相似性 来计算给定c的o的 概率 (反之亦然);
- 不断调整词向量来最大化这个概率。
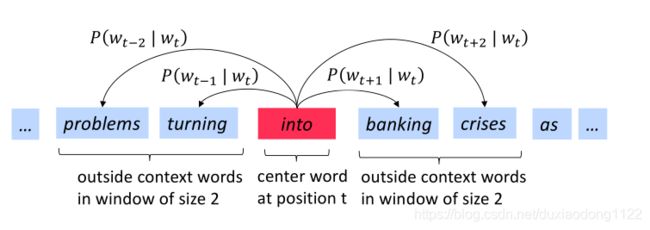
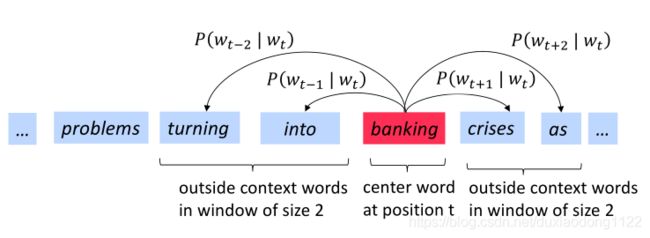
下图为窗口大小j=2时,计算上下文词的条件概率 P ( w t + j ∣ w t ) P\left(w_{t+j} | w_{t}\right) P(wt+j∣wt)的过程,center word分别为into和banking:
objective function :
对于每个位置t=1,…,T,在大小为m的固定窗口内预测上下文单词,给定中心词wj,其似然概率为:
L i k e l i h o o o d = L ( θ ) = ∏ t = 1 T ∏ − m ≤ j ≤ m j ≠ 0 P ( w t + j ∣ w t ; θ ) Likelihoood = L(\theta) = \prod^{T}_{t=1} \prod_{-m \leq j \leq m \atop j \neq 0} P(w_{t+j} | w_{t} ; \theta) Likelihoood=L(θ)=t=1∏Tj=0−m≤j≤m∏P(wt+j∣wt;θ)
由似然概率得到目标函数为:
J ( θ ) = − 1 T log L ( θ ) = − 1 T ∑ t = 1 T ∑ − m ≤ j ≤ m j ≠ 0 log P ( w t + j ∣ w t ; θ ) J(\theta)=-\frac{1}{T} \log L(\theta)=-\frac{1}{T} \sum_{t=1}^{T} \sum_{-m \leq j \leq m \atop j \neq 0} \log P\left(w_{t+j} | w_{t} ; \theta\right) J(θ)=−T1logL(θ)=−T1t=1∑Tj=0−m≤j≤m∑logP(wt+j∣wt;θ)
使用log函数的意义在于,将求累乘改为求累加;使用负号的意义在于,将极大化似然概率率转化为求损失函数最小化的问题。
如何最小化objective function:
对于每个单词w,都有两个向量表示,当w为中心词时,其词向量为v_w;当w为上下文词时,其词向量为u_w。于是,对于一个中心词c和它的一个上下文词o,得到了Word2vec prediction function:
P ( o ∣ c ) = exp ( u o T v c ) ∑ w ∈ V exp ( u w T v c ) P(o | c)=\frac{\exp \left(u_{o}^{T} v_{c}\right)}{\sum_{w \in V} \exp \left(u_{w}^{T} v_{c}\right)} P(o∣c)=∑w∈Vexp(uwTvc)exp(uoTvc)
其中,点积操作用来比较u和v之间词向量的相似性,取幂操作用来保证点积的结果为正。
Word2vec prediction function公式类似于机器学习中经常用到的softmax function:
softmax ( x i ) = exp ( x i ) ∑ j = 1 n exp ( x j ) = p i \operatorname{softmax}\left(x_{i}\right)=\frac{\exp \left(x_{i}\right)}{\sum_{j=1}^{n} \exp \left(x_{j}\right)}=p_{i} softmax(xi)=∑j=1nexp(xj)exp(xi)=pi
在最小化objective function的过程中,我们随机初始化u_w和v_w,然后使用梯度下降法进行参数的更新:
f r a c ∂ ∂ v c log P ( o ∣ c ) = ∂ ∂ v c log exp ( u o T v c ) ∑ w ∈ V exp ( u w T v c ) = ∂ ∂ v c ( log exp ( u o T v c ) − log ∑ w ∈ V exp ( u w T v c ) ) = ∂ ∂ v c ( u o T v c − log ∑ w ∈ V exp ( u w T v c ) ) = u o − ∑ w ∈ V exp ( u w T v c ) u w ∑ w ∈ V exp ( u w T v c ) \\frac{\partial}{\partial v_c}\log P(o|c) =\frac{\partial}{\partial v_c}\log \frac{\exp(u_o^Tv_c)}{\sum_{w\in V}\exp(u_w^Tv_c)}\\ =\frac{\partial}{\partial v_c}\left(\log \exp(u_o^Tv_c)-\log{\sum_{w\in V}\exp(u_w^Tv_c)}\right)\\ =\frac{\partial}{\partial v_c}\left(u_o^Tv_c-\log{\sum_{w\in V}\exp(u_w^Tv_c)}\right)\\ =u_o-\frac{\sum_{w\in V}\exp(u_w^Tv_c)u_w}{\sum_{w\in V}\exp(u_w^Tv_c)} frac∂∂vclogP(o∣c)=∂vc∂log∑w∈Vexp(uwTvc)exp(uoTvc)=∂vc∂(logexp(uoTvc)−logw∈V∑exp(uwTvc))=∂vc∂(uoTvc−logw∈V∑exp(uwTvc))=uo−∑w∈Vexp(uwTvc)∑w∈Vexp(uwTvc)uw
我们可以对上述结果重新排列如下,第一项是真正的上下文单词,第二项是预测的上下文单词。使用梯度下降法,模型的预测上下文将逐步接近真正的上下文:
f r a c ∂ ∂ v c log P ( o ∣ c ) = u o − ∑ w ∈ V exp ( u w T v c ) u w ∑ w ∈ V exp ( u w T v c ) = u o − ∑ w ∈ V exp ( u w T v c ) ∑ w ∈ V exp ( u w T v c ) u w = u o − ∑ w ∈ V P ( w ∣ c ) u w frac{\partial}{\partial v_c}\log P(o|c) =u_o-\frac{\sum_{w\in V}\exp(u_w^Tv_c)u_w}{\sum_{w\in V}\exp(u_w^Tv_c)}\\ =u_o-\sum_{w\in V}\frac{\exp(u_w^Tv_c)}{\sum_{w\in V}\exp(u_w^Tv_c)}u_w\\ =u_o-\sum_{w\in V}P(w|c)u_w frac∂∂vclogP(o∣c)=uo−∑w∈Vexp(uwTvc)∑w∈Vexp(uwTvc)uw=uo−w∈V∑∑w∈Vexp(uwTvc)exp(uwTvc)uw=uo−w∈V∑P(w∣c)uw
再对u_o进行偏微分计算,注意这里的u_o是 u_(w=0) 的简写,故可知:
∂ ∂ u o ∑ w ∈ V u w T v c = ∂ ∂ u o u o T v c = ∂ u o ∂ u o v c + ∂ v c ∂ u o u o = v c \frac{\partial}{\partial u_o}\sum_{w \in V } u_w^T v_c = \frac{\partial}{\partial u_o} u_o^T v_c = \frac{\partial u_o}{\partial u_o}v_c + \frac{\partial v_c}{\partial u_o}u_o= v_c ∂uo∂w∈V∑uwTvc=∂uo∂uoTvc=∂uo∂uovc+∂uo∂vcuo=vc
∂ ∂ u o log P ( o ∣ c ) = ∂ ∂ u o log exp ( u o T v c ) ∑ w ∈ V exp ( u w T v c ) = ∂ ∂ u o ( log exp ( u o T v c ) − log ∑ w ∈ V exp ( u w T v c ) ) = ∂ ∂ u o ( u o T v c − log ∑ w ∈ V exp ( u w T v c ) ) = v c − ∑ ∂ ∂ u o exp ( u w T v c ) ∑ w ∈ V exp ( u w T v c ) = v c − exp ( u o T v c ) v c ∑ w ∈ V exp ( u w T v c ) = v c − exp ( u o T v c ) ∑ w ∈ V exp ( u w T v c ) v c = v c − P ( o ∣ c ) v c = ( 1 − P ( o ∣ c ) ) v c \frac{\partial}{\partial u_o}\log P(o|c) =\frac{\partial}{\partial u_o}\log \frac{\exp(u_o^Tv_c)}{\sum_{w\in V}\exp(u_w^Tv_c)}\\ =\frac{\partial}{\partial u_o}\left(\log \exp(u_o^Tv_c)-\log{\sum_{w\in V}\exp(u_w^Tv_c)}\right)\\ =\frac{\partial}{\partial u_o}\left(u_o^Tv_c-\log{\sum_{w\in V}\exp(u_w^Tv_c)}\right)\\ =v_c-\frac{\sum\frac{\partial}{\partial u_o}\exp(u_w^Tv_c)}{\sum_{w\in V}\exp(u_w^Tv_c)}\\ =v_c - \frac{\exp(u_o^Tv_c)v_c}{\sum_{w\in V}\exp(u_w^Tv_c)}\\ =v_c - \frac{\exp(u_o^Tv_c)}{\sum_{w\in V}\exp(u_w^Tv_c)}v_c\\ =v_c - P(o|c)v_c\\ =(1-P(o|c))v_c ∂uo∂logP(o∣c)=∂uo∂log∑w∈Vexp(uwTvc)exp(uoTvc)=∂uo∂(logexp(uoTvc)−logw∈V∑exp(uwTvc))=∂uo∂(uoTvc−logw∈V∑exp(uwTvc))=vc−∑w∈Vexp(uwTvc)∑∂uo∂exp(uwTvc)=vc−∑w∈Vexp(uwTvc)exp(uoTvc)vc=vc−∑w∈Vexp(uwTvc)exp(uoTvc)vc=vc−P(o∣c)vc=(1−P(o∣c))vc
当P(o|c)→1,即通过中心词c我们可以正确预测上下文词o,此时我们不需要调整u_o,反之,则相应调整u_o。