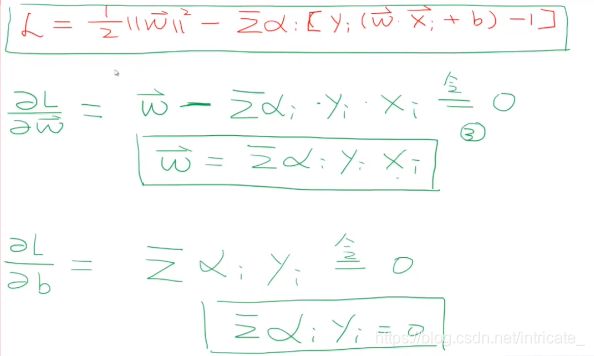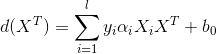机器学习笔记20-SVM
SVM 基本概念
将实例的特征向量(以二维为例)映射为空间中的一些点,就是如下图的实心点和空心点,它们属于不同的两类。
那么 SVM 的目的就是想要画出一条线,以“最好地”区分这两类点,以至如果以后有了新的点,这条线也能做出很好的分类。
![]()
画线的标准是什么?/ 什么才叫这条线的效果好?
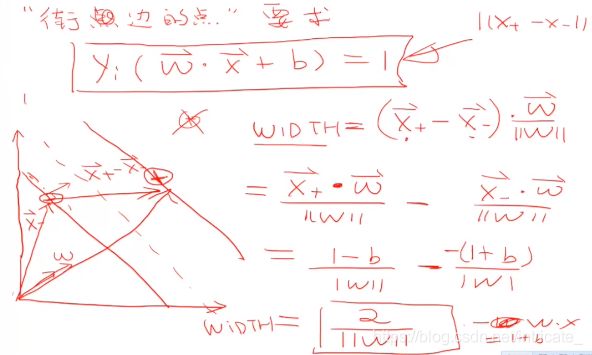
SVM 将会寻找可以区分两个类别并且能使边际(margin)最大的超平面(hyper plane)
边际(margin)是什么?
边际就是某一条线距离它两侧最近的点的距离之和。
比如下图中两条虚线构成的带状区域就是 margin,虚线是由距离中央实线最近的两个点所确定出来的。可以明显的看到但左图的 margin 比较小,右图的margin 明显变大也更接近我们的目标。
SVM 算法特性
- 训练好的模型的算法复杂度是由支持向量的个数决定的,而不是由数据的维度决定的。所以 SVM 不太容易产生 overfitting。
- SVM 训练出来的模型完全依赖于支持向量,即使训练集里面所有非支持向量的点都被去除,重复训练过程,结果仍然会得到完全一样的模型。
- 一个 SVM 如果训练得出的支持向量个数比较少,那么SVM 训练出的模型比较容易被泛化。
SVM的公式推导
首先,我们假设超平面为: ![]()
假设2维特征向量:X=(x1,x2)
把b看作额外的weight, 记作![]()
则超平面的方程为:![]()
所有超平面右上方的点满足: ![]()
所有超平面左下方的点满足:![]()
调整 weight,使超平面定义如下:
H1:![]() for
for ![]()
H1:![]() for
for ![]()
把上述两式合并得到:![]()
所有坐落在边际超平面上的点被称作支持向量(support vectors)
对于所有的支持向量,满足条件:![]()
欲找到具有“最大间隔”(maximum margin)的划分超平面,也就是找到参数w和b,使得γ最大,即:
![]()
上面的约束等价于如下约束:
![]()
利用 Karush-Kuhn-Tucker (KKT)条件和拉格朗日公式,可以推出 MMH 可以被表示为以下“决定边界 (decision boundary)”
把![]() 带入回L可以得到
带入回L可以得到
约束条件有:
![]()
最后我们得到决策边界:
l是支持向量点的个数,因为大部分的点并不是支持向量点,只有个别在边际超平面上的点才是支持向量点。那么我们就只对属于
支持向量的点进行求和;
 为支持向量点的特征值;
为支持向量点的特征值;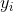 为支持向量点
为支持向量点 的类别标记,比如是+1还是-1;
的类别标记,比如是+1还是-1;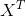 是要测试的实例,想知道它属于哪一类,带入以上方程
是要测试的实例,想知道它属于哪一类,带入以上方程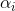 和
和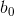 都是单一数值型参数,由以上提到的最优算法得出,
都是单一数值型参数,由以上提到的最优算法得出,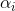 是拉格朗日乘数
是拉格朗日乘数
SVM 求解案例
sklearn 简单例子
# sklearn 库中导入 svm 模块
from sklearn import svm
# 定义三个点和标签
X = [[2, 0], [1, 1], [2,3]]
y = [0, 0, 1]
# 定义分类器,clf 意为 classifier,是分类器的传统命名
clf = svm.SVC(kernel = 'linear') # .SVC()就是 SVM 的方程,参数 kernel 为线性核函数
# 训练分类器
clf.fit(X, y) # 调用分类器的 fit 函数建立模型(即计算出划分超平面,且所有相关属性都保存在了分类器 cls 里)
# 打印分类器 clf 的一系列参数
print (clf)
# 支持向量
print (clf.support_vectors_)
# 属于支持向量的点的 index
print (clf.support_)
# 在每一个类中有多少个点属于支持向量
print (clf.n_support_)
# 预测一个新的点
print (clf.predict([[2,0]]))
输出结果:
SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape='ovr', degree=3, gamma='auto_deprecated',
kernel='linear', max_iter=-1, probability=False, random_state=None,
shrinking=True, tol=0.001, verbose=False)
[[1. 1.]
[2. 3.]]
[1 2]
[1 1]
[0]
- 可以看到 SVM 找到的支持向量是(1,1)和(2,3)两个点,和我们上面的例子是符合的
- 输出的属于支持向量的点的 index 就是 1 和 2
- 由于找到了两个支持向量分别属于正类和负类,所以输出的每个类中属于支持向量的点的个数就是 1 和 1
sklearn 划分超平面
print(__doc__)
# 导入相关的包
import numpy as np
import pylab as pl # 绘图功能
from sklearn import svm
# 创建 40 个点
np.random.seed(0) # 让每次运行程序生成的随机样本点不变
# 生成训练实例并保证是线性可分的
# np._r表示将矩阵在行方向上进行相连
# random.randn(a,b)表示生成 a 行 b 列的矩阵,且随机数服从标准正态分布
# array(20,2) - [2,2] 相当于给每一行的两个数都减去 2
X = np.r_[np.random.randn(20, 2) - [2, 2], np.random.randn(20, 2) + [2, 2]]
# 两个类别 每类有 20 个点,Y 为 40 行 1 列的列向量
Y = [0] * 20 + [1] * 20
# 建立 svm 模型
clf = svm.SVC(kernel='linear')
clf.fit(X, Y)
# 获得划分超平面
# 划分超平面原方程:w0x0 + w1x1 + b = 0
# 将其转化为点斜式方程,并把 x0 看作 x,x1 看作 y,b 看作 w2
# 点斜式:y = -(w0/w1)x - (w2/w1)
w = clf.coef_[0] # w 是一个二维数据,coef 就是 w = [w0,w1]
a = -w[0] / w[1] # 斜率
xx = np.linspace(-5, 5) # 从 -5 到 5 产生一些连续的值(随机的)
# .intercept[0] 获得 bias,即 b 的值,b / w[1] 是截距
yy = a * xx - (clf.intercept_[0]) / w[1] # 带入 x 的值,获得直线方程
# 画出和划分超平面平行且经过支持向量的两条线(斜率相同,截距不同)
b = clf.support_vectors_[0] # 取出第一个支持向量点
yy_down = a * xx + (b[1] - a * b[0])
b = clf.support_vectors_[-1] # 取出最后一个支持向量点
yy_up = a * xx + (b[1] - a * b[0])
# 查看相关的参数值
print("w: ", w)
print("a: ", a)
print("support_vectors_: ", clf.support_vectors_)
print("clf.coef_: ", clf.coef_)
# 在 scikit-learin 中,coef_ 保存了线性模型中划分超平面的参数向量。形式为(n_classes, n_features)。若 n_classes > 1,则为多分类问题,(1,n_features) 为二分类问题。
# 绘制划分超平面,边际平面和样本点
pl.plot(xx, yy, 'k-')
pl.plot(xx, yy_down, 'k--')
pl.plot(xx, yy_up, 'k--')
# 圈出支持向量
pl.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1],
s=80, facecolors='none')
pl.scatter(X[:, 0], X[:, 1], c=Y, cmap=pl.cm.Paired)
pl.axis('tight')
pl.show()
输出结果:
Automatically created module for IPython interactive environment
w: [0.90230696 0.64821811]
a: -1.391980476255765
support_vectors_: [[-1.02126202 0.2408932 ]
[-0.46722079 -0.53064123]
[ 0.95144703 0.57998206]]
clf.coef_: [[0.90230696 0.64821811]]
![]()
核方法(kernel trick)
在线性 SVM 中转化为最优化问题时求解的公式计算都是以内积(dot product)形式出现的,其中![]() 是把训练集中的向量点转化到高维的非线性映射函数,因为内积的算法复杂度非常大,所以我们利用核函数来取代计算非线性映射函数的内积。
是把训练集中的向量点转化到高维的非线性映射函数,因为内积的算法复杂度非常大,所以我们利用核函数来取代计算非线性映射函数的内积。
以下核函数和非线性映射函数的内积等同,但核函数 K 的运算量要远少于求内积。
![]()
参考:https://blog.csdn.net/qq_31347869/article/details/88071930
https://blog.csdn.net/ch18328071580/article/details/94168411