CycleGAN实现图像风格迁移的神作
论文链接:http://openaccess.thecvf.com/content_ICCV_2017/papers/Zhu_Unpaired_Image-To-Image_Translation_ICCV_2017_paper.pdf
在CycleGAN出现之前,pix2pix网络在处理image-image translation问题上比较state-of-the-art。但是pix2pix需要利用成对(pair)的数据进行模型训练,如下图所示:

成对的数据在自然界中是非常稀有的,因此pix2pix对数据的要求很高,一般而言不具备通用性。CycleGAN的出现可以解决这一问题,也就是说,CycleGAN可利用unpaired数据,在source domain X X X和target domain Y Y Y之间建立一个映射: G : X → Y G:X\rightarrow Y G:X→Y,从而使得源域 X X X的图像转化为与目标域 Y Y Y分布相似的图像。也就是说,图像 G ( X ) G(X) G(X)无法被分辨出是从 Y Y Y中采样的还是由 G G G生成的。
通过这个操作,我们就可以将自然图像转化为具有莫奈风格的图像,可以将斑马转变成普通的骏马,将冬天转变为夏天等等。也就是说,CycleGAN可以实现图像的风格迁移,更广义地来说,实现了图像间的翻译。
但是如果仅有 G : X → Y G:X\rightarrow Y G:X→Y,显然是不能完成这一任务的。因为这个映射只能确保 G ( X ) G(X) G(X)神似目标域 Y Y Y中的样本,并不能确保它与生成前的图像是对应的。举个不太恰当例子,现在的源域 X X X表示“中文”,目标域 Y Y Y表示“英文”。从 X X X中采样一个样本「你好吗」,经过 G : X → Y G:X\rightarrow Y G:X→Y得到的 G ( X ) G(X) G(X)理应是「How are you」。但是,由于该映射只是希望 G ( X ) G(X) G(X)拥有目标域“英文”的特征,所以它可以是任意一句英文,如「I’m fine」。这样就失去了translation的意义。同时,GAN网络为了保证最小化Loss,宁愿所有样本的都生成同一个输出,也不会冒险去生成多样的结果,这就造成了Mode Collapse.
为了解决这个问题,CycleGAN中引入了循环一致性损失。仅仅有 G : X → Y G:X\rightarrow Y G:X→Y是不够的,还需要再引入一个映射 F : Y → X F:Y\rightarrow X F:Y→X,以将 G ( X ) G(X) G(X)重新映射回源域 X X X,并衡量 F ( G ( X ) ) F(G(X)) F(G(X))与 X X X之间的差距,希望这个差距越小越好。这种思想相当于是一种Autoencoder, G ( X ) G(X) G(X)相当于AE中的编码,如果这个编码能够还原出与 X X X相似的 F ( G ( X ) ) F(G(X)) F(G(X)),那么就可以认为 G ( X ) G(X) G(X)虽然接近目标域分布 Y Y Y,但原始图像上的语义特征并没丢失。
有了这一重约束,上面例子中的「你好吗」就不会翻译成「I’m fine」,因为「I’m fine」的语义特征和「你好吗」不同,不易从「I’m fine」还原到「你好吗」。
因此,整个网络的模型架构如下图所示:
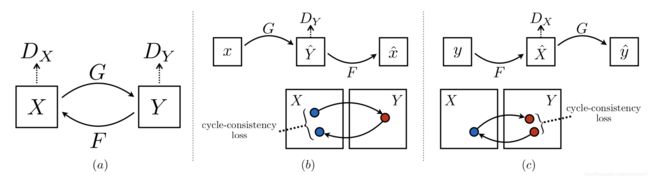
图(a)展示的是 G : X → Y G:X\rightarrow Y G:X→Y和 F : Y → X F:Y\rightarrow X F:Y→X两个生成器映射过程, D Y D_{Y} DY鉴别的是 G ( X ) G(X) G(X)属于目标域分布 Y Y Y的确定性,和GAN中的鉴别器原理一致; D X D_{X} DX与之同理;图(b)展示的正向循环一致性损失,即 x → G ( x ) → F ( G ( x ) ) ≈ x x\rightarrow G(x)\rightarrow F(G(x))\approx x x→G(x)→F(G(x))≈x;图(c)展示的反向循环一致性损失,即 y → F ( y ) → G ( F ( y ) ) ≈ y y\rightarrow F(y)\rightarrow G(F(y))\approx y y→F(y)→G(F(y))≈y。
因此整个训练过程的损失函数定义如下:
L ( G , F , D X , D Y ) = L G A N ( G , D Y , X , Y ) + L G A N ( F , D X , Y , X ) + λ L c y c ( G , F ) L(G,F,D_{X},D_{Y})=L_{GAN}(G,D_{Y},X,Y)+L_{GAN}(F,D_{X},Y,X)+\lambda L_{cyc}(G,F) L(G,F,DX,DY)=LGAN(G,DY,X,Y)+LGAN(F,DX,Y,X)+λLcyc(G,F)
其中前两项是常规生成对抗网络中的损失函数,最后一项是循环一致性损失函数, λ \lambda λ是一个调节系数。对于前两项,这里采用了LSGAN的思想,可以进一步表达为:
L L S G A N ( G , D Y , X , Y ) = E y ∼ p d a t a ( y ) [ ( D Y ( y ) − 1 ) 2 ] + E x ∼ p d a t a ( x ) [ D Y ( G ( x ) ) 2 ] L_{LSGAN}(G,D_{Y},X,Y)=E_{y\sim p_{data}(y)}[(D_{Y}(y)-1)^{2}]+E_{x\sim p_{data}(x)}[D_{Y}(G(x))^{2}] LLSGAN(G,DY,X,Y)=Ey∼pdata(y)[(DY(y)−1)2]+Ex∼pdata(x)[DY(G(x))2]
L L S G A N ( F , D X , X , Y ) = E x ∼ p d a t a ( x ) [ ( D X ( x ) − 1 ) 2 ] + E y ∼ p d a t a ( y ) [ D X ( G ( y ) ) 2 ] L_{LSGAN}(F,D_{X},X,Y)=E_{x\sim p_{data}(x)}[(D_{X}(x)-1)^{2}]+E_{y\sim p_{data}(y)}[D_{X}(G(y))^{2}] LLSGAN(F,DX,X,Y)=Ex∼pdata(x)[(DX(x)−1)2]+Ey∼pdata(y)[DX(G(y))2]
对于循环一致性损失,其相当于自动编码器的重构误差,可以表达为:
L c y c ( G , F ) = E x ∼ p d a t a ( x ) [ ∣ ∣ F ( G ( x ) ) − x ∣ ∣ 1 ] + E y ∼ p d a t a ( y ) [ ∣ ∣ G ( F ( y ) ) − y ∣ ∣ 1 ] L_{cyc}(G,F)=E_{x\sim p_{data}(x)}[||F(G(x))-x||_{1}]+E_{y\sim p_{data}(y)}[||G(F(y))-y||_{1}] Lcyc(G,F)=Ex∼pdata(x)[∣∣F(G(x))−x∣∣1]+Ey∼pdata(y)[∣∣G(F(y))−y∣∣1]
CycleGAN的理论到这里就差不多了,可以看出理论并不是很复杂,而是非常精妙。巧妙的引入了循环一致性改变了网络的结构,不再需要成对的数据,从而使得CycleGAN非常的generalized。下面是论文中CycleGAN的一些实验结果:
根据上图,CycleGAN可以实现斑马和马,冬天夏天即橙子苹果间的转换,论文中还做了很多有趣的实验,如图像增强,将随机拍摄的自然图像转换为专业的摄影图片,或融入莫奈的画风。
但是CycleGAN仍然存在一些问题,例如在将马转化为斑马的时候,很可能会将骑马的人也加上斑纹。因为原始训练集都是大自然中的马,因此模型学习不到人的相关知识。笔者也做过CycleGAN的实验,发现有些时候模型会将一些比较突出的背景也加上斑纹,如石头,醒目的植物等等,因此在稳定性方面还是有提升空间的。此外,CycleGAN不易实现形状的改变,比如将猫改成狗,外表形状上必然要发生变化,而CycleGAN不易实现,这也是可以改进之处。
总结
CycleGAN的精髓就是利用循环一致性,对网络进行改造,使得网络类似于两个相互对抗的自动编码器,从而实现了用unpaired数据进行图像到图像的翻译。理论不难,主要是这个idea太巧妙了。