机器学习1:一元线性回归

机器学习1:一元线性回归

原理

一元线性回归

y = b + k
这个方程对应的图像是一条直线，称作回归线。其中，
k为回归线的斜率， b为回归线的截距。

代价函数

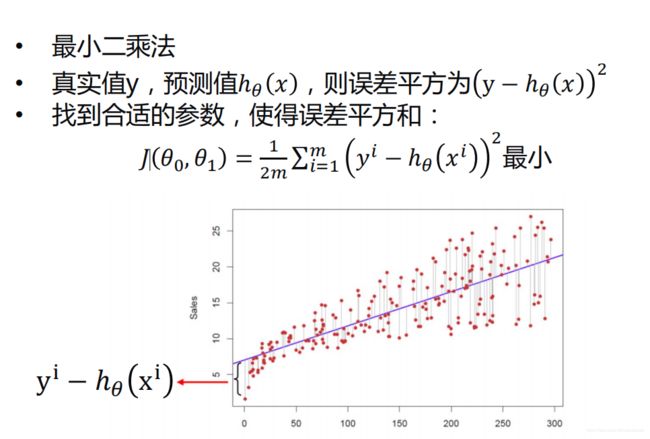
线性回归本质就是寻找代价函数最小的斜率和截距

相关系数

决定系数

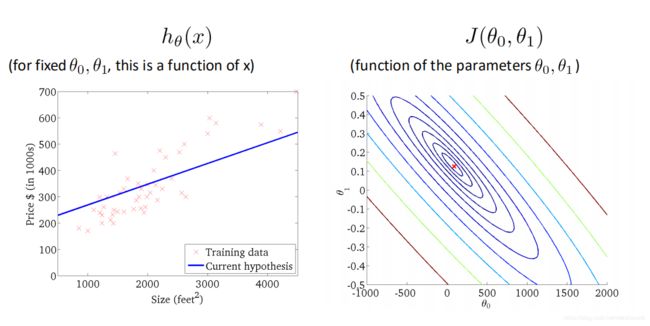
梯度下降法

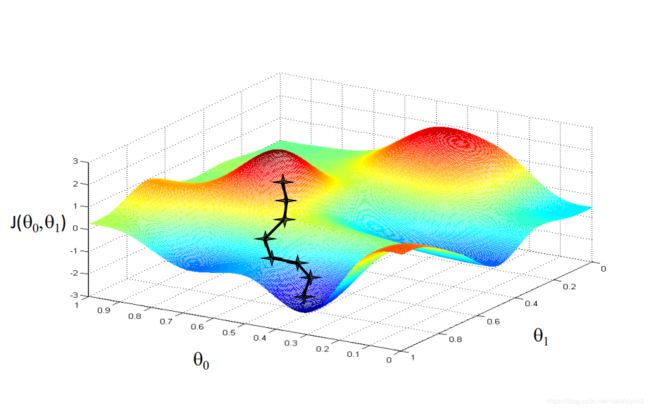
不同的初始点可能会有不同的路径

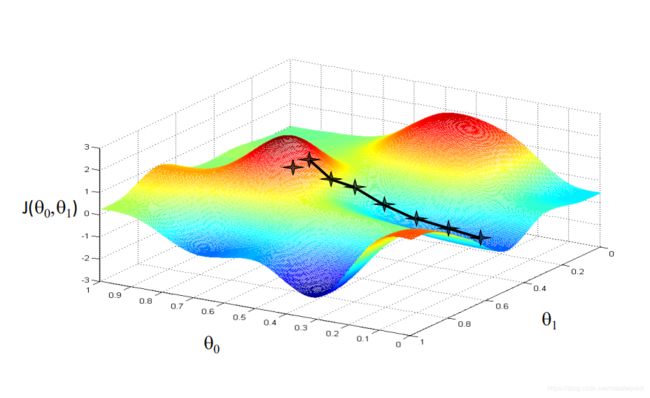
梯度下降法求一元回归方程斜率和截距

学习率不能太小，也不能太大，可以多尝试一些值
0.1,0.03,0.01,0.003,0.001,0.0003,0.0001…
有可能会陷入局部极小值

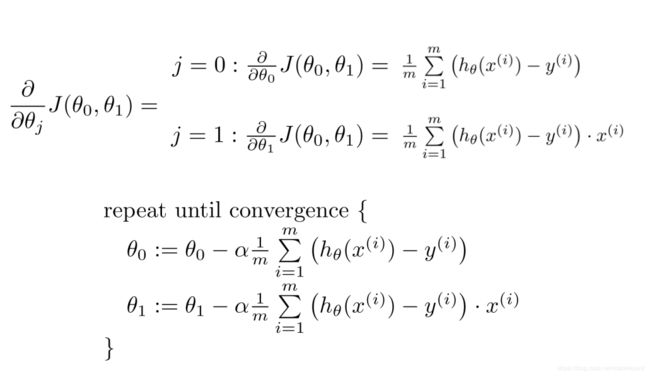
算法实现

import numpy as np
import matplotlib.pyplot as plt
#载入数据
data=np.genfromtxt("data.csv",delimiter=",")
x_data=data[:,0]
y_data=data[:,1]
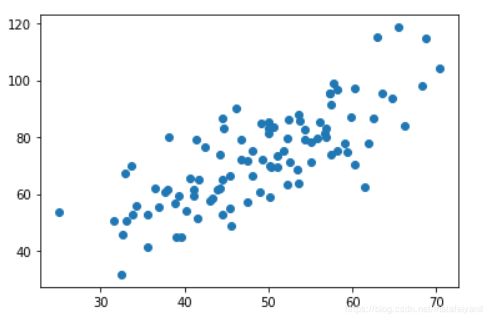
plt.scatter(x_data,y_data)
plt.show()

#学习率
lr=0.0001
#初始斜率
k=0
#初始截距
b=0
#最大迭代次数
epochs=50

#最小二乘法
def compute_error(b,k,x_data,y_data):
    totalError=0
    for i in range(0,len(x_data)):
        totalError+=(y_data[i]-(k*x_data[i]+b))**2    #求代价函数
    return totalError/float(len(x_data))/2

def gradient_descent_runner(x_data,y_data,b,k,lr,epochs):
    #计算总数据量
    m=float(len(x_data))
    #循环epochs次
    for i in range(epochs):
        b_grad=0
        k_grad=0
        #计算梯度的总和再求平均
        for j in range(0,len(x_data)):
            b_grad += (1/m)*(((k*x_data[j])+b)-y_data[j])
            k_grad += (1/m)*x_data[j]*(((k*x_data[j])+b)-y_data[j])
        #更新b和k
        b=b-(lr*b_grad)
        k=k-(lr*k_grad)
    return b,k       
 
print("Starting b = {0}, k = {1}, error = {2}".format(b, k, compute_error(b, k, x_data, y_data)))
print("Running...")
b, k = gradient_descent_runner(x_data, y_data, b, k, lr, epochs)
print("After {0} iterations b = {1}, k = {2}, error = {3}".format(epochs, b, k, compute_error(b, k, x_data, y_data)))

#画图
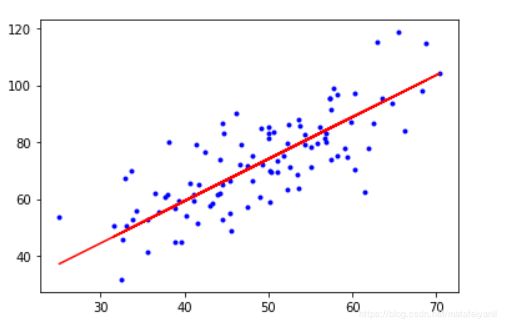
plt.plot(x_data, y_data, 'b.')
plt.plot(x_data, k*x_data + b, 'r')
plt.show()       

sklearn算法实现

from sklearn.linear_model import LinearRegression  #导入线性回归模型
import numpy as np
import matplotlib.pyplot as plt

#载入数据
data=np.genfromtxt("data.csv",delimiter=",")
x_data=data[:,0]
y_data=data[:,1]
plt.scatter(x_data,y_data)
plt.show()
print(x_data.shape)

x_data=data[:,0,np.newaxis]  #加上一个维度
print(x_data.shape)

x_data=data[:,0,np.newaxis]
y_data=data[:,1,np.newaxis]
#创建并拟合模型
model=LinearRegression()
model.fit(x_data,y_data)

#画图
plt.plot(x_data, y_data, 'b.')
plt.plot(x_data, model.predict(x_data) , 'r')
plt.show()