深度目标检测网络中关于anchor的神之问(配代码详解)(一)
目录
Faster RCNN中的anchor的得出原理是什么?
Faster RCNN中给定一张图如何计算anchor的数量?
如何改变Faster RCNN中anchor的数量和尺寸?
YOLO中的anchor的得出原理是什么?
YOLO的anchor机制和RPN的anchor有什么不同?
Faster RCNN中的anchor的得出原理是什么?
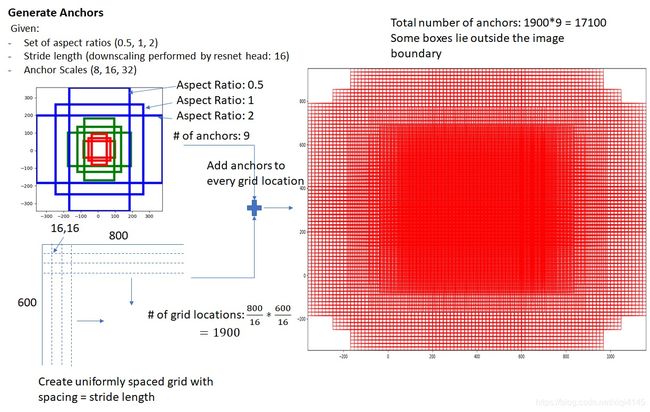
固定的,长宽比为:0.5;1;2,尺度为:8;16;32
其实从源码上看,可分为两个步骤:
1)保持anchor的面积不变,但是改变长宽的比例。此步有三个比例,最终得到三个不同长宽比的预测框
2):保持长宽的比例不变,但是进行scale的缩放,从而改变比例。此步是在上一步的基础上进行的,也是有三个比例,将每一个长宽比的预测框,缩放三次,那么最后,就得到了9个预测框(下面的介绍为方便理解统一称呼anchor为预测框)了!
配着代码看个清楚:
首先,看下总函数:
def generate_anchors(base_size=16, ratios=[0.5, 1, 2],
scales=2 ** np.arange(3, 6)):
"""
Generate anchor (reference) windows by enumerating aspect ratios X
scales wrt a reference (0, 0, 15, 15) window.
"""
base_anchor = np.array([1, 1, base_size, base_size]) - 1
ratio_anchors = _ratio_enum(base_anchor, ratios)
anchors = np.vstack([_scale_enum(ratio_anchors[i, :], scales)
for i in xrange(ratio_anchors.shape[0])])
return anchors其中,base_anchor是默认的anchor初始值为[0, 0, 15, 15]。ratio_anchors得出的是上面介绍的1)的结果,就是进行按长宽比例进行变换的三个预测框的信息。再下面的经过_scale_enum函数来处理后的结果,对应着2)所介绍的,生成了不同缩放比例的9个预测框信息。
PS:这里有一个很重要的点要注意,代码里面表示的anchor的描述向量的意义,是指:[框的左上角的横坐标,框的左上角的竖坐标,框的右下角的横坐标和框的右下角的横坐标],而不是一般理解的[框的长,框的宽,框的中心坐标x,框的中心坐标y]
对1)环节的实现:
ratio_anchors = _ratio_enum(base_anchor, ratios)
def _ratio_enum(anchor, ratios):
"""
Enumerate a set of anchors for each aspect ratio wrt an anchor.
"""
w, h, x_ctr, y_ctr = _whctrs(anchor)
size = w * h
size_ratios = size / ratios
ws = np.round(np.sqrt(size_ratios))
hs = np.round(ws * ratios)
anchors = _mkanchors(ws, hs, x_ctr, y_ctr)
return anchors这个是对根据长宽比的不同来实现变换的,首先,经过一个_whctrs函数将原理根据左上角,右下角描述预测框的方式,变为用[框的长,框的宽,框的中心坐标x,框的中心坐标y]来表示。接着,计算面积size,通过除以不同的长宽比,变换出新的ws,hs,而中心点的x,y坐标是不用变换的。这样就得到了新的三个(根据ratio参数的个数来决定)预测框了。最后再通过_mkanchors函数将之变换回[框的左上角的横坐标,框的左上角的竖坐标,框的右下角的横坐标和框的右下角的横坐标]的形式。并把结果返回,这个过程,使预测框有1个变成了3个。
PS:这个地方我一直保留有疑问,就是为啥好多博客上都说这个过程是长宽比改变,但保存面积不变?我看的明明是变的啊?三组ws*hs的结果不一样,和原来的w*h也不一样啊
下面说说上面遇到的两个函数_whctrs和_mkanchors,看主线思路的可直接跳过。
_whctrs函数收到一个根据左右角坐标来表示框的向量。先根据向量的内容计算出来w,h,x,y然后再返回出去就行了。
def _whctrs(anchor):
"""
Return width, height, x center, and y center for an anchor (window).
"""
w = anchor[2] - anchor[0] + 1
h = anchor[3] - anchor[1] + 1
x_ctr = anchor[0] + 0.5 * (w - 1)
y_ctr = anchor[1] + 0.5 * (h - 1)
return w, h, x_ctr, y_ctr_mkanchors函数可以说是_whctrs函数的逆过程,
def _mkanchors(ws, hs, x_ctr, y_ctr):
"""
Given a vector of widths (ws) and heights (hs) around a center
(x_ctr, y_ctr), output a set of anchors (windows).
"""
ws = ws[:, np.newaxis]
hs = hs[:, np.newaxis]
anchors = np.hstack((x_ctr - 0.5 * (ws - 1),
y_ctr - 0.5 * (hs - 1),
x_ctr + 0.5 * (ws - 1),
y_ctr + 0.5 * (hs - 1)))
return anchors
将之再反向计算回去,以[框的左上角的横坐标,框的左上角的竖坐标,框的右下角的横坐标和框的右下角的横坐标]的传递,方便后面的计算。
对2)的实现:
anchors = np.vstack([_scale_enum(ratio_anchors[i, :], scales)
for i in xrange(ratio_anchors.shape[0])])
def _scale_enum(anchor, scales):
"""
Enumerate a set of anchors for each scale wrt an anchor.
"""
w, h, x_ctr, y_ctr = _whctrs(anchor)
ws = w * scales
hs = h * scales
anchors = _mkanchors(ws, hs, x_ctr, y_ctr)
return anchors这个的话也不难,主要是_scale_enum函数的操作,还是通过_whctrs函数将之变成[w,h,x,y]的表达形式,然后乘以对应的scales系数,得到新的ws和hs,和变换长宽比的时候一样,也都是不改变中心坐标的x和y,最后,返回anchors值。
需要再解释的地方就是,在总函数哪里,列表里加循环那步有点复杂,解释起来就是,ratio_anchors[i, :]将上步得到的3个框信息,逐一的导入,i就是表示第几个框(ratio_anchors.shape[0])),后面的scales系数,就是对应着三个缩放系数。
最后得到的是九个anchors。
完整代码
https://github.com/rbgirshick/py-faster-rcnn/blob/781a917b378dbfdedb45b6a56189a31982da1b43/lib/rpn/generate_anchors.py
# --------------------------------------------------------
# Faster R-CNN
# Copyright (c) 2015 Microsoft
# Licensed under The MIT License [see LICENSE for details]
# Written by Ross Girshick and Sean Bell
# --------------------------------------------------------
import numpy as np
def generate_anchors(base_size=16, ratios=[0.5, 1, 2],
scales=2 ** np.arange(3, 6)):
"""
Generate anchor (reference) windows by enumerating aspect ratios X
scales wrt a reference (0, 0, 15, 15) window.
"""
base_anchor = np.array([1, 1, base_size, base_size]) - 1
ratio_anchors = _ratio_enum(base_anchor, ratios)
anchors = np.vstack([_scale_enum(ratio_anchors[i, :], scales)
for i in xrange(ratio_anchors.shape[0])])
return anchors
def _whctrs(anchor):
"""
Return width, height, x center, and y center for an anchor (window).
"""
w = anchor[2] - anchor[0] + 1
h = anchor[3] - anchor[1] + 1
x_ctr = anchor[0] + 0.5 * (w - 1)
y_ctr = anchor[1] + 0.5 * (h - 1)
return w, h, x_ctr, y_ctr
def _mkanchors(ws, hs, x_ctr, y_ctr):
"""
Given a vector of widths (ws) and heights (hs) around a center
(x_ctr, y_ctr), output a set of anchors (windows).
"""
ws = ws[:, np.newaxis]
hs = hs[:, np.newaxis]
anchors = np.hstack((x_ctr - 0.5 * (ws - 1),
y_ctr - 0.5 * (hs - 1),
x_ctr + 0.5 * (ws - 1),
y_ctr + 0.5 * (hs - 1)))
return anchors
def _ratio_enum(anchor, ratios):
"""
Enumerate a set of anchors for each aspect ratio wrt an anchor.
"""
w, h, x_ctr, y_ctr = _whctrs(anchor)
size = w * h
size_ratios = size / ratios
ws = np.round(np.sqrt(size_ratios))
hs = np.round(ws * ratios)
anchors = _mkanchors(ws, hs, x_ctr, y_ctr)
return anchors
def _scale_enum(anchor, scales):
"""
Enumerate a set of anchors for each scale wrt an anchor.
"""
w, h, x_ctr, y_ctr = _whctrs(anchor)
ws = w * scales
hs = h * scales
anchors = _mkanchors(ws, hs, x_ctr, y_ctr)
return anchors
if __name__ == '__main__':
import time
t = time.time()
a = generate_anchors()
print time.time() - t
print a
from IPython import embed;
embed()
Faster RCNN中给定一张图如何计算anchor的数量?
以源码为例,源码初始坐标为[0, 0, 15, 15]意味着第一个anchors对应的预测框的左上角坐标为(0,0),右下角的坐标为(15,15)。那么这个框移动的时候,以边长为步长,覆盖过的区域就不再覆盖了,所以,可以断步长为16(应知计算机里面是从0就开始计数的,0到15,是一共16)那么,给定一个输入图片,可以产生多少个预测框呢?假设给定一个600*800的大小的图片,那么先计算可移动的覆盖次数即:(800/16)*(600/16)=1900,那么,每次覆盖产生9个anchors,则最终的结果是1900*9=17100,一共17100个anchor.对应效果如上图右边。
如何改变Faster RCNN中anchor的数量和尺寸?
还是要对应源码来解释的,Faster R-CNN源码产生anchors的部分,位置$Faster RCNN/lib/rpn/generate_anchors.py:
def generate_anchors(base_size=16, ratios=[0.5, 1, 2],
scales=2 ** np.arange(3, 6)):(详细见第一个问题),从这里可以看出ratios的设定决定了产生的anchors的长宽比,scales设定决定了产生的anchosr的放缩尺度,anchors产生的个数是由这俩个设定的个数的乘积决定的,要是想改变个数就改变scales、ratios的参数个数即可。
YOLO中的anchor的得出原理是什么?
首先设置anchor的目的是为了使得预测框与ground truth的IOU更好(这个就好比是中心思想,一切操作的源头,一定记着)
那么是怎么实现的呢?YOLO(准确的说是v2和v3的版本)的anchor机制是借鉴Faster RCNN的RPN来设定的,但又稍有不同,YOLO中的anchor的数量不像是RPN那样提前人工设置好的,而是,根据所检测的数据集的情况通过用K-means++算法通过聚类的方式得出来的。那么这里有个问题,就是明明中心思想是为了使预测框和GT的IOU更好,为啥和anchor的数量有关系呢?这就要解释anchor的机制,在RPN中,anchor的数量是由scales、ratios两个参数共同的乘积决定的(具体见上问),其中ratios就代表着长宽比,那么,引用到YOLO里面来,为了让预测框和TGT有更好的IOU,就需要对ratios这个参数进行设置,使得使用的anchor的预测框的尺寸跟最多的GT尺寸保持一种“天然”重合的趋势,即让开始的时候就把anchor的预测框形状设置成训练数据中最普遍的GT长宽比的大小,这样得出来的结果不就可以有更好的IOU了吗?那么,就对ratios进行设置,那么怎么设置呢?总不能像RPN那样提前规定好一个固定的长宽比进行设定吧,不同的训练集有不同分布的GT长宽分布,不能要针对不同对象选取不同的对策,故而,采用了用聚类的方式,找出所训练数据集中最普遍的长宽比,继而,用这个长宽比来作为anchor预测框的长宽比。那么在YOLO中,并没有关于scales缩放的操作,只是调整了长宽比,假设最后得出了n组长宽比,那么最后,决定的每个anchor对应的预测框数量就是n*1(scales认为是1)个了,那么大神们嘴里说的5个anchor指的就是再yolov2版本的时候,人家是用COCO数据集来作为训练集,那么对这个数据集通过聚类聚出了5个聚类中心,即有5个可以涵盖整个数据集框分布的最常见长宽比,那么对应的,就是所谓的“5”了。
PS:因为加入了anchor机制,v2可以预测的框的数量变为了(13*13*num_anchors)相比于v1中的(7*7*2),YOLOv2的召回率大大提升,由原来的81%升至88%。
下面通过代码记下anchor的是怎么通过聚类得到这个“5”的。
下面这个是个总的函数,用来执行k-means++的聚类,思路很简单,先把数据集给读进去,然后,把数据集里的所有的框,给放到一个集合里面,然后,从集合里面初始化一个最开始的聚类中心,然后,根据这个中心,反复的进行迭代,将离它最近的(这个距离的测量是根据计算IOU来代替的)框的长宽,累加起来再求平均,就是下一次迭代的聚类中心了,反复n(自己可设定)轮,直到迭代轮数停止,或等到计算的聚类中心满足了所设定的IOU距离,就停止,那么,剩下的距离中心,就是这个数据集所得的anchor的长宽比了。
# 计算给定bounding boxes的n_anchors数量的centroids
# label_path是训练集列表文件地址
# n_anchors 是anchors的数量
# loss_convergence是允许的loss的最小变化值
# grid_size * grid_size 是栅格数量
# iterations_num是最大迭代次数
# plus = 1时启用k means ++ 初始化centroids
def compute_centroids(label_path,n_anchors,loss_convergence,grid_size,iterations_num,plus):
boxes = []
label_files = []
f = open(label_path)
for line in f:
label_path = line.rstrip().replace('images', 'labels')
label_path = label_path.replace('JPEGImages', 'labels')
label_path = label_path.replace('.jpg', '.txt')
label_path = label_path.replace('.JPEG', '.txt')
label_files.append(label_path)
f.close()
for label_file in label_files:
f = open(label_file)
for line in f:
temp = line.strip().split(" ")
if len(temp) > 1:
boxes.append(Box(0, 0, float(temp[3]), float(temp[4])))
if plus:
centroids = init_centroids(boxes, n_anchors)
else:
centroid_indices = np.random.choice(len(boxes), n_anchors)
centroids = []
for centroid_index in centroid_indices:
centroids.append(boxes[centroid_index])
# iterate k-means
centroids, groups, old_loss = do_kmeans(n_anchors, boxes, centroids)
iterations = 1
while (True):
centroids, groups, loss = do_kmeans(n_anchors, boxes, centroids)
iterations = iterations + 1
print("loss = %f" % loss)
if abs(old_loss - loss) < loss_convergence or iterations > iterations_num:
break
old_loss = loss
for centroid in centroids:
print(centroid.w * grid_size, centroid.h * grid_size)
# print result
for centroid in centroids:
print("k-means result:\n")
print(centroid.w * grid_size, centroid.h * grid_size)下面这部分是计算初始化的聚类中心的,先是随机的选一个框来作为初始化的框,centroid_index=np.random.choice(boxes_num, 1);然后,计算所有框到这个框的距离,并累加起来,将累加起来的值,乘上一个(0,1)之间的随机数,变成一个阈值,distance_thresh = sum_distance*np.random.random(),然后,再把刚刚的所有框都遍历一遍,如果大于这个阈值就认为下一个聚类中心点的聚类中心就是它了(这个过程中,所求的聚类中心的数量是需要提前设定好的,),这也是本着K-Means++算法在聚类中心的初始化过程中的基本原则是使得初始的聚类中心之间的相互距离尽可能远来进行,最后那个随机数选阈值的思路,学名叫做:以概率选择距离最大的样本作为新的聚类中心。
# 使用k-means ++ 初始化 centroids,减少随机初始化的centroids对最终结果的影响
# boxes是所有bounding boxes的Box对象列表
# n_anchors是k-means的k值
# 返回值centroids 是初始化的n_anchors个centroid
def init_centroids(boxes,n_anchors):
centroids = []
boxes_num = len(boxes)
centroid_index = np.random.choice(boxes_num, 1)
centroids.append(boxes[centroid_index])
print(centroids[0].w,centroids[0].h)
for centroid_index in range(0,n_anchors-1):
sum_distance = 0
distance_thresh = 0
distance_list = []
cur_sum = 0
for box in boxes:
min_distance = 1
for centroid_i, centroid in enumerate(centroids):
distance = (1 - box_iou(box, centroid))
if distance < min_distance:
min_distance = distance
sum_distance += min_distance
distance_list.append(min_distance)
distance_thresh = sum_distance*np.random.random()
for i in range(0,boxes_num):
cur_sum += distance_list[i]
if cur_sum > distance_thresh:
centroids.append(boxes[i])
print(boxes[i].w, boxes[i].h)
break
return centroids最后,就是通过迭代来选取新的聚类中心的过程了,思路也是一样,计算最小距离,并记录下来,然后,把这些进行累加new_centroids[i].w /= len(groups[i]) new_centroids[i].h /= len(groups[i],再平均求和,就是新聚类中心的w和h了。
# 进行 k-means 计算新的centroids
# boxes是所有bounding boxes的Box对象列表
# n_anchors是k-means的k值
# centroids是所有簇的中心
# 返回值new_centroids 是计算出的新簇中心
# 返回值groups是n_anchors个簇包含的boxes的列表
# 返回值loss是所有box距离所属的最近的centroid的距离的和
def do_kmeans(n_anchors, boxes, centroids):
loss = 0
groups = []
new_centroids = []
for i in range(n_anchors):
groups.append([])
new_centroids.append(Box(0, 0, 0, 0))
for box in boxes:
min_distance = 1
group_index = 0
for centroid_index, centroid in enumerate(centroids):
distance = (1 - box_iou(box, centroid))
if distance < min_distance:
min_distance = distance
group_index = centroid_index
groups[group_index].append(box)
loss += min_distance
new_centroids[group_index].w += box.w
new_centroids[group_index].h += box.h
for i in range(n_anchors):
new_centroids[i].w /= len(groups[i])
new_centroids[i].h /= len(groups[i])
return new_centroids, groups, loss完整代码
https://github.com/PaulChongPeng/darknet/blob/master/tools/k_means_yolo.py
# coding=utf-8
# k-means ++ for YOLOv2 anchors
# 通过k-means ++ 算法获取YOLOv2需要的anchors的尺寸
import numpy as np
# 定义Box类,描述bounding box的坐标
class Box():
def __init__(self, x, y, w, h):
self.x = x
self.y = y
self.w = w
self.h = h
# 计算两个box在某个轴上的重叠部分
# x1是box1的中心在该轴上的坐标
# len1是box1在该轴上的长度
# x2是box2的中心在该轴上的坐标
# len2是box2在该轴上的长度
# 返回值是该轴上重叠的长度
def overlap(x1, len1, x2, len2):
len1_half = len1 / 2
len2_half = len2 / 2
left = max(x1 - len1_half, x2 - len2_half)
right = min(x1 + len1_half, x2 + len2_half)
return right - left
# 计算box a 和box b 的交集面积
# a和b都是Box类型实例
# 返回值area是box a 和box b 的交集面积
def box_intersection(a, b):
w = overlap(a.x, a.w, b.x, b.w)
h = overlap(a.y, a.h, b.y, b.h)
if w < 0 or h < 0:
return 0
area = w * h
return area
# 计算 box a 和 box b 的并集面积
# a和b都是Box类型实例
# 返回值u是box a 和box b 的并集面积
def box_union(a, b):
i = box_intersection(a, b)
u = a.w * a.h + b.w * b.h - i
return u
# 计算 box a 和 box b 的 iou
# a和b都是Box类型实例
# 返回值是box a 和box b 的iou
def box_iou(a, b):
return box_intersection(a, b) / box_union(a, b)
# 使用k-means ++ 初始化 centroids,减少随机初始化的centroids对最终结果的影响
# boxes是所有bounding boxes的Box对象列表
# n_anchors是k-means的k值
# 返回值centroids 是初始化的n_anchors个centroid
def init_centroids(boxes,n_anchors):
centroids = []
boxes_num = len(boxes)
centroid_index = np.random.choice(boxes_num, 1)
centroids.append(boxes[centroid_index])
print(centroids[0].w,centroids[0].h)
for centroid_index in range(0,n_anchors-1):
sum_distance = 0
distance_thresh = 0
distance_list = []
cur_sum = 0
for box in boxes:
min_distance = 1
for centroid_i, centroid in enumerate(centroids):
distance = (1 - box_iou(box, centroid))
if distance < min_distance:
min_distance = distance
sum_distance += min_distance
distance_list.append(min_distance)
distance_thresh = sum_distance*np.random.random()
for i in range(0,boxes_num):
cur_sum += distance_list[i]
if cur_sum > distance_thresh:
centroids.append(boxes[i])
print(boxes[i].w, boxes[i].h)
break
return centroids
# 进行 k-means 计算新的centroids
# boxes是所有bounding boxes的Box对象列表
# n_anchors是k-means的k值
# centroids是所有簇的中心
# 返回值new_centroids 是计算出的新簇中心
# 返回值groups是n_anchors个簇包含的boxes的列表
# 返回值loss是所有box距离所属的最近的centroid的距离的和
def do_kmeans(n_anchors, boxes, centroids):
loss = 0
groups = []
new_centroids = []
for i in range(n_anchors):
groups.append([])
new_centroids.append(Box(0, 0, 0, 0))
for box in boxes:
min_distance = 1
group_index = 0
for centroid_index, centroid in enumerate(centroids):
distance = (1 - box_iou(box, centroid))
if distance < min_distance:
min_distance = distance
group_index = centroid_index
groups[group_index].append(box)
loss += min_distance
new_centroids[group_index].w += box.w
new_centroids[group_index].h += box.h
for i in range(n_anchors):
new_centroids[i].w /= len(groups[i])
new_centroids[i].h /= len(groups[i])
return new_centroids, groups, loss
# 计算给定bounding boxes的n_anchors数量的centroids
# label_path是训练集列表文件地址
# n_anchors 是anchors的数量
# loss_convergence是允许的loss的最小变化值
# grid_size * grid_size 是栅格数量
# iterations_num是最大迭代次数
# plus = 1时启用k means ++ 初始化centroids
def compute_centroids(label_path,n_anchors,loss_convergence,grid_size,iterations_num,plus):
boxes = []
label_files = []
f = open(label_path)
for line in f:
label_path = line.rstrip().replace('images', 'labels')
label_path = label_path.replace('JPEGImages', 'labels')
label_path = label_path.replace('.jpg', '.txt')
label_path = label_path.replace('.JPEG', '.txt')
label_files.append(label_path)
f.close()
for label_file in label_files:
f = open(label_file)
for line in f:
temp = line.strip().split(" ")
if len(temp) > 1:
boxes.append(Box(0, 0, float(temp[3]), float(temp[4])))
if plus:
centroids = init_centroids(boxes, n_anchors)
else:
centroid_indices = np.random.choice(len(boxes), n_anchors)
centroids = []
for centroid_index in centroid_indices:
centroids.append(boxes[centroid_index])
# iterate k-means
centroids, groups, old_loss = do_kmeans(n_anchors, boxes, centroids)
iterations = 1
while (True):
centroids, groups, loss = do_kmeans(n_anchors, boxes, centroids)
iterations = iterations + 1
print("loss = %f" % loss)
if abs(old_loss - loss) < loss_convergence or iterations > iterations_num:
break
old_loss = loss
for centroid in centroids:
print(centroid.w * grid_size, centroid.h * grid_size)
# print result
for centroid in centroids:
print("k-means result:\n")
print(centroid.w * grid_size, centroid.h * grid_size)
label_path = "/raid/pengchong_data/Data/Lists/paul_train.txt"
n_anchors = 5
loss_convergence = 1e-6
grid_size = 13
iterations_num = 100
plus = 0
compute_centroids(label_path,n_anchors,loss_convergence,grid_size,iterations_num,plus)
YOLO的anchor机制和RPN的anchor有什么不同?
1.YOLO不是像RPN那样手选的先验框,而是通过k-means得到的。
2.YOLO的anchor 仅对长宽比进行了规定,并没有尺度的设置。
3.YOLO所得到的anchor框,是针对每个分割好的小区域进行的(需要做个转换),而RPN针对的是整个图片。
由于从标记文件的width,height计算出的anchor boxes的width和height都是相对于整张图片的比例,而YOLOv2通过anchor boxes直接预测bounding boxes的坐标时,坐标是相对于栅格边长的比例(0到1之间),因此要将anchor boxes的width和height也转换为相对于栅格边长的比例。转换公式如下:
w=anchor_width*input_width/downsamples ;h=anchor_height*input_height/downsamples
例如:
卷积神经网络的输入为416*416时,YOLOv2网络的降采样倍率为32,假如k-means计算得到一个anchor box的anchor_width=0.2,anchor_height=0.6,则:
w=0.2*416/32=0.2*13=2.6;h=0.6*416/32=0.6*13=7.8