排序算法总结
文章目录
- 排序算法总结
- 冒泡排序
- 算法思想:
- 代码实现
- 时间复杂度及稳定性
- 插入排序
- 算法思想
- 代码实现
- 时间复杂度及稳定性
- 选择排序
- 算法思想
- 代码实现
- 时间复杂度及稳定性
- 归并排序
- 算法思想
- 代码实现
- 时间复杂度及稳定性
- 快速排序
- 堆排序
排序算法总结
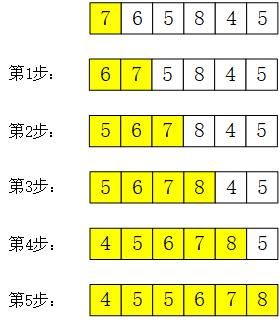
以数组arr = [7,6,5,8,4,5],升序排列为例:
冒泡排序
算法思想:
对数组进行n次遍历,每次交换相邻位置上左边比右边大的数,每次找到一个最大的数。
代码实现
def bubble_sort(arr,i):
for i in range(i):
if arr[i] > arr[i+1]:
arr[i],arr[i+1] = arr[i+1],arr[i]
if __name__ == '__main__':
arr = [7, 6, 5, 8, 4, 5]
for i in range(len(arr)-1,0,-1):
bubble_sort(arr,i)
print(arr)
时间复杂度及稳定性
时间复杂度:O(n^2)。一共进行了2次for循环。
稳定性:稳定。每次与相邻位置做比较进行交换,两数相等不做交换。
插入排序
算法思想
对数组进行n次遍历,每一次前(i-1)个数是有序的,比较第i个数与前i-1个数,将其插入到合适的位置。
代码实现
def insert_sort(arr,i):
value = arr[i]
while(i > 0):
if value < arr[i-1]:
arr[i] = arr[i-1]
i -= 1
else:
break
arr[i] = value
if __name__ == '__main__':
arr = [7, 6, 5, 8, 4, 5]
for i in range(1,len(arr),1):
insert_sort(arr,i)
print(arr)
时间复杂度及稳定性
时间复杂度:O(n^2)。进行了2次for循环。
稳定性:稳定。
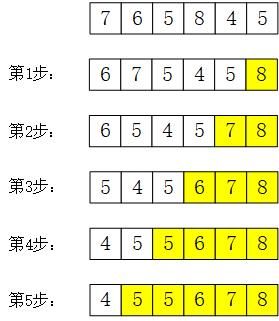
选择排序
算法思想
对数组进行n次遍历,每次选出剩余元素中最小的。
代码实现
def select_sort(arr, i):
for j in range(i, len(arr)):
if arr[j] < arr[i]:
arr[i],arr[j] = arr[j],arr[i]
if __name__ == '__main__':
arr = [7, 6, 5, 8, 4, 5]
for i in range(len(arr)):
select_sort(arr, i)
print(arr)
时间复杂度及稳定性
时间复杂度:O(n^2),进行了2次for循环;
稳定性:不稳定。假设arr = [5,5,4,5,5],存在4与第一个5的交换。
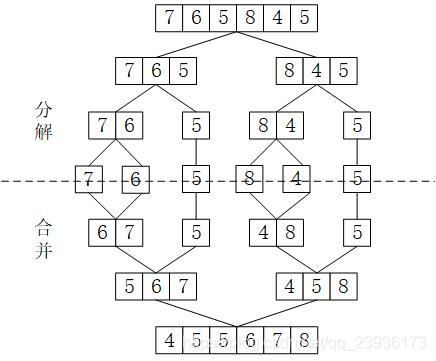
归并排序
详解:归并排序及“归并”思想的应用
算法思想
对数组进行不断的分解,分解到仅剩一个元素为止;然后,按照从小到大的规则进行合并。
代码实现
def merge_sort(arr):
# 递归的对数组进行分解,仅剩一个元素时,停止分解
if len(arr) == 1:
return arr
mid = len(arr) // 2
left = merge_sort(arr[:mid])
right = merge_sort(arr[mid:])
# 对数组进行合并
arr = merge(left, right)
return arr
def merge(left, right):
i = j = 0
arr = []
while (i < len(left) and j < len(right)):
if left[i] <= right[j]:
arr.append(left[i])
i += 1
else:
arr.append(right[j])
j += 1
while (i < len(left)):
arr.append(left[i])
i += 1
while (j < len(right)):
arr.append(right[j])
j += 1
return arr
if __name__ == '__main__':
arr = [2, 3, 8, 6, 7, 4, 5]
print(merge_sort(arr))
时间复杂度及稳定性
时间复杂度:O(n* log(n))。一共进行了n次分解,将数组分解为单个元素;之后,进行了log(n)次合并,得到有序数组。
稳定性:稳定。
快速排序
荷兰国旗与快速排序
堆排序
堆排序及复杂度分析