【小白学AI】随机森林 全解 （从bagging到variance）

文章转自公众号【机器学习炼丹术】，关注回复“炼丹”即可获得海量免费学习资料哦！

---

为什么现在还要学习随机森林？

随机森林中仍有两个未解之谜（对我来说）。随机森林采用的bagging思想中怎么得到的62.3% 以及 随机森林和bagging的方法是否有区别。

随机森林(Random Forest)就是通过集成学习的思想将多棵决策树集成的一种算法。基本单元是决策树。随机森林算法的提出也是为了改善决策树容易存在过拟合的情况。

1 随机森林

习惯上，我们将众多分类器(SVM、Logistic回归、决策树等)所组成的“总的分类器”，叫做随机森林。随机森林有两个关键词，一个是“随机”，一个是“森林”。森林就是成百上千棵树，体现了集成的思想，随机将会在下面总结到。

2 bagging

Bagging，其实就是bootstrap aggregating的缩写, 两者是等价的，其核心就是有放回抽样。

【bagging具体步骤】

1. 从大小为n的样本集中有放回地重采样选出n个样本；（没错就是n个样本抽取n个）
2. 在所有属性上，对这n个样本建立分类器(ID3信息增益、C4.5信息增益率、CART基尼系数、SVM、Logistic回归等)
3. 重复以上两步m次，即获得了m个分类器；
4. 将预测数据放在这m个分类器上，最后根据这m个分类器的投票结果，决定数据属于哪一类。

3 神秘的63.2%

一般被大家知晓的是：随机森林中每一次采样的比例是63.2%。 这个比例到底是怎么确定的呢？

在某手的面试中，我被问到了这个相关的问题，奈何学艺不精，哎。后来苦苦研究15分钟，终于得到答案，现在分享给大家。

---

bagging的最初的说法其实是：n个样本从中有放回抽样n次，这种条件下，势必会有抽取到相同样本的可能性，那么抽取到不同样本的期望值是多少呢？其实大家心里可能会有答案了，没错就是0.632n。

我们假设$U(k)$表示第k次抽样抽取到不同样本的概率。那么$U(k-1)$则表示第k-1次抽样抽取到不同样本的概率。

• 第k-1次抽样到不同样本的概率：$U(k-1)$
• 第k-1次抽样时，有$nU(k-1)$个样本还没有被抽取
• 第k次抽样时，还有$nU(k-1)-U(k-1)$的样本没有抽取
• 因此$U(k)=\frac{n-1}{n}U(k-1)=(\frac{n-1}{n}{)}^{k-1}U(1)$
• $U(1)=1$,第一次抽样的数据一定不会重复

因此k次放回抽样的不同样本的期望值为：
${\sum }_{i=1}^{k-1}U(i)=1+\frac{n-1}{n}+(\frac{n-1}{n}{)}^2+\dots$

利用等比数列的性质，得到：
${\sum }_{i=1}^{k-1}U(i)=(1-(\frac{n-1}{n}{)}^k)n$

当n足够大，并且k=n的情况下，上面的公式等于
$$(1-(\frac{n-1}{n}{)}^k)n=(1-\frac{1}{e})n\approx 0.632n$$

所以证明完毕，每一次bagging采样重复抽取n次其实只有63.2%的样本会被采样到。

---

4 随机森林 vs bagging

随机森林(Random Forest)在Bagging基础上进行了修改。 具体步骤可以总结如下:

1. 从训练样本集中采用Bootstrap的方法有放回地重采样选出n个样本，即每棵树的训练数据集都是不同的 ，里面包含重复的训练样本（这意味着随机森林并不是按照bagging的0.632比例采样 ）；

2. 从所有属性中有选择地选出K个属性，选择最佳属性作为节点建立CART决策树；

3. 重复以上步骤m次，即建立了m棵CART决策树

4. 这m个CART形成随机森林，通过投票表决分类结果，决定数据是属于哪一类。

随机森林(Random Forest)的随机性主要体现在两方面，一方面是样本随机，另一方面是属性随机。样本随机的原因是如果样本不随机，每棵树的训练数据都一样，那么最终训练出的分类结果也是完全一样的。

5 投票策略

1. 少数服从多数
2. 一票否决
3. 听说还有贝叶斯平均的方法。但是我没有过多了解。一般还是用少数服从多数的吧。

6 随机森林的特点

6.1 优点

1. 在当前的算法中，具有极好的准确率
2. 能够运行在大数据上
3. 能够处理具有高维特征的输入样本，不需要降维
4. 能够计算各个特征的重要度
5. 能够防止过拟合

6.2 bias 与 variance

说到机器学习模型的误差，主要就是bias和variance。

• Bias：如果一个模型的训练错误大，然后验证错误和训练错误都很大，那么这个模型就是高bias。可能是因为欠拟合，也可能是因为模型是弱分类器。

• Variance：模型的训练错误小，但是验证错误远大于训练错误，那么这个模型就是高Variance，或者说它是过拟合。

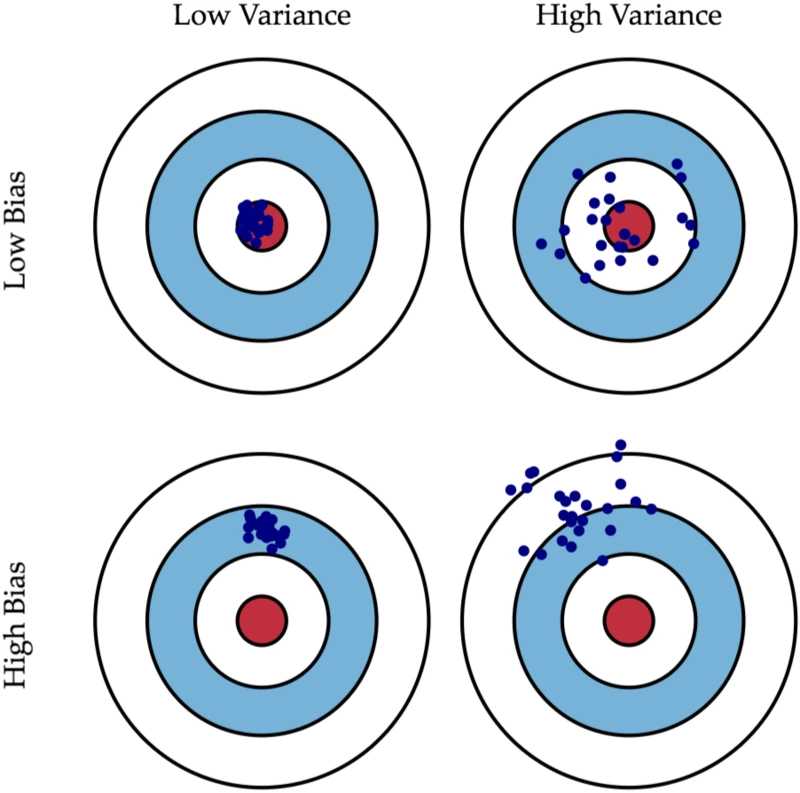
这个图中，左上角是低偏差低方差的，可以看到所有的预测值，都会落在靶心，完美模型；

右上角是高偏差，可以看到，虽然整体数据预测的好像都在中心，但是波动很大。

【高偏差vs高方差】
在机器学习中，因为偏差和方差不能兼顾，所以我们一般会选择高偏差、低方差的左下角的模型。稳定性是最重要的，宁可所有的样本都80%正确率，也不要部分样本100%、部分50%的正确率。个人感觉，稳定性是学习到东西的体现，高方差模型与随机蒙的有什么区别？

6.3 随机森林降低偏差证明

上面的可能有些抽象，这里用RandomForest(RF)来作为例子：
随机森林是bagging的集成模型，这里：
$RF(x)=\frac{1}{B}{\sum }_{i=1}^B{T}_{i,z_i}(x)$

• RF(x)表示随机森林对样本x的预测值；
• B表示总共有B棵树；
• $z_i$表示第i棵树所使用的训练集，是使用bagging的方法，从所有训练集中进行行采样和列采样得到的子数据集。

这里所有的$z$，都是从所有数据集中随机采样的，所以可以理解为都是服从相同分布的。所以不断增加B的数量，增加随机森林中树的数量，是不会减小模型的偏差的。
【个人感觉，是因为不管训练再多的树，其实就那么多数据，怎么训练都不会减少，这一点比较好理解】

【RF是如何降低偏差的？】
直观上，使用多棵树和bagging，是可以增加模型的稳定性的。怎么证明的？

---

我们需要计算$Var(T(x))$

假设不同树的$z_i$之间的相关系数为$\rho$,然后每棵树的方差都是${\sigma }^2$.

先复习一下两个随机变量相加的方差如何表示：
$Var(aX+bY)=a^{2}Var(X)+b^{2}Var(Y)+2abcov(X,Y)$

• Cov(X,Y)表示X和Y的协方差。协方差和相关系数不一样哦，要除以X和Y的标准差：
  $\rho =\frac{cov(X,Y)}{{\sigma }_X{\sigma }_Y}$

下面转成B个相关变量的方差计算，是矩阵的形式：

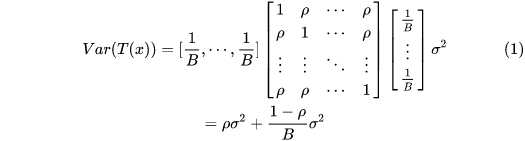
很好推导的，可以试一试。

这样可以看出来了，RF的树的数量越多，RF方差的第二项会不断减小，但是第一项不变。也就是说，第一项就是RF模型偏差的下极限了。

【总结】

• 增加决策树的数量B，偏差不变；方差减小；
• 增加决策树深度，偏差减小；$\rho$减小，${\sigma }^2$增加；
• 增加bagging采样比例，偏差减小；$\rho$增加，${\sigma }^2$增加；

【bagging vs boost】
之前的文章也提到过了boost算法。

GBDT中，在某种情况下，是不断训练之前模型的残差，来达到降低bias的效果。虽然也是集成模型，但是可以想到，每一个GBDT中的树，所学习的数据的分布都是不同的，这意味着在GBDT模型的方差会随着决策树的数量增多，不断地增加。

• bagging的目的：降低方差；
• boost的目的：降低偏差