【点分治】【点分治序】BZOJ3784 树上的路径

分析：

首先，定义点分治序为：
每次找到重心后，以重心为根，当前子树的DFS序。每一个重心的DFN序次连接，就组成了点分治序。显然，点分治序的长度是$NlogN$级的。

现在，根据一般点分治的方式，在以X为重心时，我们要找到所有子树中的点，与X的距离。对某个点u而言，如果考虑u->x->v的一条路径，则v不能在与u相同的子树中。且这个v在点分治序上的位置是相邻的。

于是，就可以找到对任意一个点u，经过某个重心，到达另一部分的点的最长路径。

找到全局最长路径后，显然这条路径可以加入答案。现在考虑次大的路径：把最长路径拆分为两部分，其余不变。

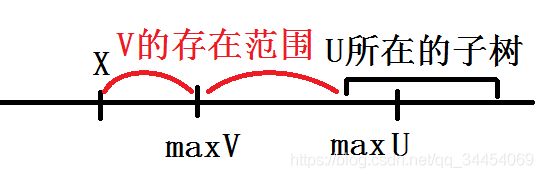
找最大值用RMQ即可。答案可以用堆来维护，弹出M次即可。

#include
#include
#include
#include
#include
#include
#define SF scanf
#define PF printf
#define MAXN 50010
using namespace std;
vector<int> a[MAXN],w[MAXN];
int n,m,cnt,tot;
int dist[MAXN*20];
int siz[MAXN],maxsiz[MAXN];
struct node{
	int l,r,dis,ans,pos;
	bool operator <(const node &a) const {
		if(ans!=a.ans)
			return ans<a.ans;
		if(dis!=a.dis)
			return dis<a.dis;
		if(l!=a.l)
			return l<a.l;
		return r<a.r;
	}
}que[MAXN*40];
priority_queue<node> q;
bool used[MAXN];
int find_g(int x,int fa,int siz1){
	siz[x]=1;
	maxsiz[x]=0;
	int g=-1;
	for(int i=0;i<int(a[x].size());i++){
		int u=a[x][i];
		if(used[u]||u==fa)
			continue;
		int g1=find_g(a[x][i],x,siz1);
		siz[x]+=siz[u];
		maxsiz[x]=max(maxsiz[x],siz[u]);
		if(g==-1||maxsiz[g]>maxsiz[g1])
			g=g1;
	}
	maxsiz[x]=max(maxsiz[x],siz1-siz[x]);
	if(g==-1||maxsiz[g]>maxsiz[x])
		g=x;
	return g;
}
int dfs(int x,int fa,int l,int r,int len){
	int siz=1;
	dist[++cnt]=len;
//	PF("<%d %d %d %d %d>\n",x,tot,l,r,len);
	que[++tot].l=l;
	que[tot].r=r;
	que[tot].dis=len;
	for(int i=0;i<int(a[x].size());i++){ 
		int u=a[x][i];
		if(used[u]||u==fa)
			continue;
		siz+=dfs(a[x][i],x,l,r,len+w[x][i]);
	}
	return siz;
}
void solve(int x){
	used[x]=1;
	dist[++cnt]=0;
//	PF("[%d %d]\n",x,cnt);
	int las=cnt;
	for(int i=0;i<int(a[x].size());i++){
		if(used[a[x][i]])
			continue;
		siz[a[x][i]]=dfs(a[x][i],x,las,cnt,w[x][i]);
	}
	for(int i=0;i<int(a[x].size());i++)
		if(used[a[x][i]]==0)
			solve(find_g(a[x][i],x,siz[a[x][i]]));
}
int get_max(int x,int y){
	if(dist[x]>dist[y])
		return x;
	return y;	
}
int bits[MAXN*20],gr[MAXN*20][20];
int query(int l,int r){
	int len=r-l+1;
	int k=bits[len];
	return get_max(gr[l][k],gr[r-(1<<k)+1][k]);	
}
int main(){
	int u,v,val;
	SF("%d%d",&n,&m);
	for(int i=1;i<n;i++){
		SF("%d%d%d",&u,&v,&val);
		a[u].push_back(v);
		a[v].push_back(u);
		w[u].push_back(val);
		w[v].push_back(val);
	}
	solve(find_g(1,0,n));
	for(int i=1;i<=cnt;i++)
		gr[i][0]=i;
	for(int i=1;i<20;i++)
		for(int j=1;j<=cnt;j++)
			gr[j][i]=get_max(gr[j][i-1],gr[min(cnt,j+(1<<(i-1)))][i-1]);
	
	for(int i=2;i<=cnt;i++)
		bits[i]=bits[i/2]+1;
	
//	for(int i=1;i<=cnt;i++)
//		PF("%d ",dist[i]);
//	PF("\n");
	for(int i=1;i<=tot;i++){
		que[i].pos=query(que[i].l,que[i].r);
		que[i].ans=dist[que[i].pos]+que[i].dis;
//		PF("[%d %d %d %d %d]\n",que[i].l,que[i].r,que[i].dis,que[i].pos,que[i].ans);
		q.push(que[i]);
	}
	while(m--){
		node nx=q.top();
		q.pop();
		PF("%d\n",nx.ans);
		if(nx.l!=nx.pos){
			que[++cnt]=nx;
			que[cnt].r=nx.pos-1;
			que[cnt].pos=query(que[cnt].l,que[cnt].r);
			que[cnt].ans=dist[que[cnt].pos]+que[cnt].dis;
			q.push(que[cnt]);
		}
		if(nx.r!=nx.pos){
			que[++cnt]=nx;
			que[cnt].l=nx.pos+1;
			que[cnt].pos=query(que[cnt].l,que[cnt].r);
			que[cnt].ans=dist[que[cnt].pos]+que[cnt].dis;
			q.push(que[cnt]);
		}
	}
}