小白科研笔记：作为普通卷积概念上的延伸——认识流形稀疏卷积

1. 引言

最近看一些3D目标检测算法（比如之前分析的CVPR2020的SA-SSD），发现它们都调用spconv这个库。spconv对应Facebook在CVPR2018发的一篇文章。文章全名是3D Semantic Segmentation with Submanifold Sparse Convolutional Networks。文章核心创新点是提出了子流形上的稀疏卷积层（对Submanifold Sparse Convolution直译，简称为SSCN）。别看Submanifold Sparse Convolution这个名字很高大上，其实它只是普通卷积的一种推广，用于处理稀疏高维数据，比如稀疏点云。这篇博客主要介绍流形稀疏卷积。我会按照自己的理解去尽可能简单的讲解流形稀疏卷积。

2. 流形稀疏卷积网络

2.1 提取点云特征的一些方法

深度学习需要提取目标对象的特征。对于二维图像，提取操作主要是做卷积。但是对于三维点云，提取特征就变成一个困难的事情，因为三维点云是稀疏和没有结构的。为了提取具有稀疏结构的点云特征，研究者们想出了很多办法，比如PointNet系列，深度连续卷积，边缘卷积，点云卷积，等等。这里所介绍的流形稀疏卷积就是一种不太一样的方法。

2.2 普通卷积处理稀疏数据的窘境

普通卷积处理稀疏数据会面临两个窘境：

1. 容易提取到失真的特征（从稀疏的数据中提取出稠密的特征）；
2. 产生不必要的计算（普通卷积会重头到尾算一遍，而稀疏数据很多地方是空洞）。

首先解释一下普通卷积计算量的问题。先拿2D卷积举个例子。假定2D卷积核的尺寸（Kernel Size）是3，卷积参数步长（Stride）是1。输入特征图通道是$m$个。输出特征图通道是$n$个。对一个特征图上的目标像素，做一次卷积操作，需要用到$3^{2}mn$次乘法。如果特征图是$d$维，就需要用到$d$维卷积核做卷积运算。假设这个卷积核的尺寸和步长跟之前一样。再假定输入输出特征图的通道数不变。那么做一次$d$维卷积运算，需要用到$3^{d}mn$次乘法。可以发现卷积计算复杂度会随着维度变化而做指数级的增长。如果输入特征图在$d$维空间是稀疏的话，完全没有必要在$3^d$空间（指一个边长为3的$d$维立方块）内遍历所有离散点，只需要考虑$3^d$空间那些有值的特征点即可。这就引出了作者的一个定义，即Active。在$3^d$空间内，对应有值特征的点记作Active，而无值特征的点记作Inactive。

图1：普通卷积提取稀疏数据特征的示意图

再解释一下普通卷积提取稀疏数据特征为什么会失真。作者举出一个二维空间下的例子，并放出一张示意图，如图1所示。左图是稀疏二维数据。白点是有值区域。灰点是无值区域。中间这个图是对左图进行一次卷积的结果。右图是对左图进行两次卷积的结果。可以发现，随着卷积层的增加，原本稀疏的数据会变得越来越稠密。所以使用普通卷积的深度网络，很可能从稀疏的数据中学出“稠密”的特征，这种特征会破坏原始数据的稀疏原貌。从图上看，这个圆环逐渐膨胀，最终变成一个油炸圈。作者称它为“子流形膨胀问题”（submanifold dilation problem）。怎么会跟流形扯上关系呢？可以认为二维空间下，左图的圆环可以看作是一维的流形。从左到右，这就是一个“膨胀”的流形。

我对流形不太了解。上面的讨论只是一个通俗解释。

基于上述两种情况，使用普通卷积不能高效精确地处理稀疏数据。于是乎稀疏卷积就应运而生了。

2.3 稀疏卷积

稀疏卷积和普通卷积一样，需要定义核的尺寸$f$以及卷积步长$s$（$f$是个奇数），以及输入通道数$m$和输出通道数$n$。作者定义稀疏卷积符号为$SC(m,n,f,s)$。和普通卷积一样，稀疏卷积在处理$d$维数据时候的感受野是$f^d$（指一个边长为$f$的$d$维立方块）。我假设输入是一个$A_1\times A_2\times ...\times A_d\times m$的张量$T_{in}$。经过稀疏稀疏卷积后，输出一个$B_1\times B_2\times ...\times B_d\times n$的张量$T_{out}$。和普通卷积一样，$A_i$和$B_i$满足一个约束条件：$B_i=(A_i-f+s)/s，i=1,2,...,d$。这些是稀疏卷积和普通卷积一样的地方。

下面就开始阐述稀疏卷积的不一样的地方。

特殊操作一：维护正常卷积计算——空值补零

为了方便说明，我来假设一个场景，比如我想计算$T_{in}$中的一个元素$t_{in}=T_{in}(a_1,a_2,...,a_d,m_0)$的稀疏卷积值。按卷积定义，我会提取以$t_{in}$为中心在$f^d$空间内的所有值跟$f^d$大小的核做点乘。如果$T_{in}$是非常稀疏的，稀疏卷积会把目标位置$t_{in}$所在的$f^d$空间内，空洞的位置补充为零。补零后再按照普通卷积的定义做计算。这倒不是什么神奇的操作，一般人都会这么想吧。

特殊操作二：维护特征稀疏性——强制清零

为了维护输入特征的稀疏性，作者设计了一个子流形稀疏卷积（是对 submanifold sparse convolution的直译），简称为$SSCN(m,n,f,s)$。$SSCN(m,n,f,s)$是$SCN(m,n,f,s=1)$的一种改进版。$SCN(m,n,f,s=1)$的输出尺寸满足关系：$B_i=A_i-f+1，i=1,2,...,d$。为了使输出的尺寸跟输入的尺寸一致，作者在输入张量$T_{in}$上做零值补充（Zero Padding），即在$d$维中的每一个维前和后补充$(f-1)/2$个零。因为$f$是奇数，所以$(f-1)/2$是个整数。那么有，

$B_i=A_i+2\ast (f-1)/2-f+1=A_i$

这样一来，稀疏卷积输出的张量尺寸和输入张量是一样的（除了通道数）。$T_{out}$会比$T_{in}$更“膨胀”，如图1所示，因为原本零值的地方会受感受野之内有值区域的影响而卷积出非零值（联系卷积的定义，思考看看）。为了维护原特征的稀疏性（原本零值的地方卷积后应该还是零值），记$T_{in}$中零值的区域为$D_{zero}$，在$T_{out}$中把$D_{zero}$区域的值重写为零即可。这也不是什么神奇的操作，强制清零后，卷积后的特征图和卷积前的特征图是一样稀疏的，维持了submanifold的几何特性（有点强行解释的味道）。

使用子流形稀疏卷积的效果如图2所示。考虑到零的乘法运算可以不予考虑，那么$d$维稀疏卷积需要大概$amn$个乘法运算，其中$a$是感受野内非零值元素的个数。它要比普通卷积的运算复杂度小。因此稀疏卷积解决了普通卷积面临的两个窘境。

图2：使用$SSCN$的计算结果，卷积之前是一个环，稀疏卷积之后也是一个环，没改变几何性质

特殊操作三：配套服务——与稀疏卷积相配套的激活池化BN层

在深度学习中，普通卷积常常和激活函数（Activation Functions），池化层（Pooling Layers），BN（Batch Normalization）配合起来使用，以发挥巨大的作用。对于稀疏卷积而言，是不是也可以和激活函数，池化层，BN配合起来使用呢？作者的回答是肯定的，但是要做一些小小的修改。

首先说激活函数。考虑到数据是稀疏的，没必要对空洞位置使用激活函数，所以主要对有值的位置使用激活函数。再说池化层。如果是Max Pooling的话，不需要修改。如果是Average Pooling的话，仅计算有值位置的平均值。对于BN，也只是对有值区域做正则化的操作。

总之，这些改动都是顺其自然的。

2.3 稀疏卷积的计算细节

稀疏卷积的输入是稀疏的特征图，输出的也是一个稀疏的特征图。因此没有必要用一块完整的内存无差别地存储特征图中全部的值。只需要存储那些有值的位置即可。

以输入的稀疏特征图$T_{in}$为例。设稀疏特征图中非零值元素的个数为$a$个。作者把稀疏的特征图$T_{in}$编码为一个$a\times m$特征矩阵$M_{in}$和一个哈希表$H_{in}$（Hashing Table，使用哈希表可以快速查找，从稀疏张量建立哈希表，利用了SparseHash这个库）。特征矩阵存放着输入特征图中所有非零的特征，$m$表示输入特征图的通道数。哈希表是一个键值对（Key-Value）组成的列表。Key指的是特征矩阵的行索引（在$0$到$a-1$整数范围之内）。Value表示对应元素在$T_{in}$中的索引，是一个$d$维向量。

输出的稀疏特征图$T_{out}$同样编码为$M_{out}$和$H_{out}$。考虑到稀疏卷积维护输入特征图的稀疏性，$H_{out}=H_{in}$。$M_{out}$是一个$a\times n$的矩阵，$n$是输出特征图的通道数。$M_{out}$初始化为一个零矩阵。在行索引上，$M_{out}$和$M_{in}$有着等同的意义。

这样编码还是不够的。以输入的稀疏特征图$T_{in}$为例。设非零值元素的集合为$S=\{s_i{\}}_{i=1}^a$。对于任一个元素$s_i$，我怎么知道元素$s_i$的感受野内有哪些位置在集合$S$中呢？对$s_i$，满足这样要求的集合记为$R(s_i)$。设$s_j\in R(s_i)$，那么$s_j$到$s_i$的曼哈顿距离$M(s_i,s_j)$一定是小于等于卷积核的大小$f$的。

$For$ $s_i\in S,$ $find$ $s_j\in R(s_i)$ $in$ $S$ $to$ $make$ $sure$ $that$ $M(s_i,s_j)\le f$

为了找$s_j$，最简单的办法就是遍历剩下的$a-1$个位置去计算曼哈顿距离。这样一个边遍历边计算的过程用到了哈希表（使用哈希表，应该不是用我说的这个最简单的方法找$R(s_i)$，原文貌似没有具体交代，另外我对哈希表也不熟）。而集合$\{R(s_i){\}}_{i=1}^a$称之为rule book。对于$s_i$，知道$R(s_i)$后，后续操作就是做卷积运算中求积求和的计算了。

注释：这是我对原文4.2节Implementation的一个粗糙认识。可能有不对的地方。

2.4 稀疏卷积网络搭建

使用稀疏卷积网络，作者给出FCN网络和U-Net网络的搭建示意图。输入数据不是点云，而是体素化的点云（那种“我的世界”中的块块，每一个块块有int型的三维坐标）。

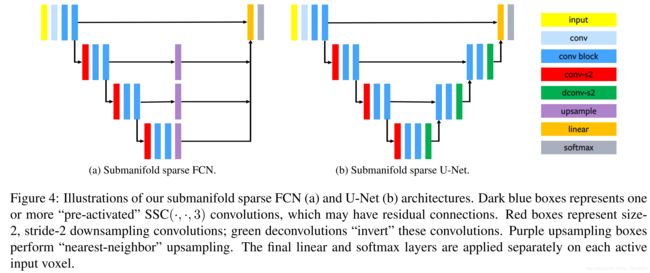
图3：使用稀疏卷积网络的FCN网络和U-Net网络的搭建示意图

深蓝色的方框conv block是$SSC(\cdot ,\cdot ,3)$的卷积组合。其他颜色的方框都是平常操作。

3. 结束语

下面是个人胡扯时间。

我对稀疏卷积关注不多。只是在分析代码偶然发现这篇论文的。流形稀疏卷积是普通卷积的推广，用于提取稀疏特征。为了提高计算效率，流形稀疏卷积使用了哈希表。在这篇文章之前也有很多papers都在讨论稀疏卷积，这篇文章把稀疏卷积的技术变得更加成熟，写成一个通用工具库spconv，供很多做点云深度学习的研究者使用。从理论上看，它的创新并不是很大，只是对普通卷积做了一丁点改动。从工程上看，它的出现完善了稀疏数据的处理。这是篇不错的文章。