[gdgzoi] 小肥猪

Description

有k头小肥猪，你每次要给他们一些饲料，重复n次。

每次给的饲料用m个操作表示：

• 操作1：（1 x）给第x头猪一份饲料；
• 操作2：（2 x y）把第x头猪的饲料给第y头猪（第x头猪就没有饲料了）；
• 操作3：（3 x）把第x头猪的饲料加倍；

给你k、m、n和m个操作，回答操作过后每头猪有多少份饲料。

Input

第1行三个数：k、m、n；
第2~m+1行每行一个操作。

Output

1行m个数：操作后每头猪的饲料个数（模10000）。

Sample Input

3 4 3
1 3
1 2
2 3 1
3 2

Sample Output

3 14 0

HINT

 

【提示】

第一次操作后：1 2 0

第二次操作后：2 6 0

第三次操作后：3 14 0

【数据范围】

对于50%的数据：n≤10^4；

对于100%的数据：k≤10，m≤10，n≤10^10；

 

题目给出一系列操作，要求我们维护一组数并循环n次，考虑到数据范围，我们很容易想到运用矩阵快速幂维护

因此我们可以构建一个(k+1)*(k+1)大小的矩阵A来存储操作，构建另一个同样大小的矩阵B存储猪的信息，由于操作有三种，我们可以另开三个矩阵表示操作，由于矩阵乘法具有交换律和结合律，每个操作表示的矩阵与A相乘，最后便能得到m次操作后的总状态，幂n-1方后就是最终状态，再用这时的A乘B便可得到操作完成后猪的信息了

如何维护矩阵？假设猪有4头，我们可以得出一下矩阵(i,j均从0开始)

B：其中只有第0列储存信息，1-3行表示每头猪，0行用于+1操作

A矩阵与三个操作的矩阵均初始化为单位矩阵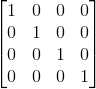：行对应每头将被更改的猪，同一行的每列对应该头猪的更改和第几头有关

对于每个操作，我们修改矩阵并与A相乘，表示操作合并完成，再把更改的部分变回去

对于操作一：对x +1,则将(x,0)变为1

对于操作二：对x->y,则将(x,x)变为0，(y,x)变为1

对于操作三：对x*2,则将(x,x)变为2

注意相乘时操作矩阵在前，A在后（行乘列），快速幂后得到最终矩阵A乘B即可（A在前）

 

贴上代码

#include
#include
#define LL long long
using namespace std;
const int mod=10000;
struct matrix //用结构体存矩阵
{
    LL m[11][11];
}ans,res,bas1,bas2,bas3,pig;//ans为A，pig为B，bas表示三种操作
void buildmatrix(LL n)//矩阵初始化
{
    for(LL i=0;i<=n;i++) ans.m[i][i]=bas1.m[i][i]=bas2.m[i][i]=bas3.m[i][i]=1;
}
matrix mul(matrix a,matrix b,LL n)//矩阵相乘
{
    matrix tmp;
    for(LL i=0;i<=n;i++)
        for(LL j=0;j<=n;j++)
            tmp.m[i][j]=0;
    for(LL i=0;i<=n;i++)
        for(LL j=0;j<=n;j++)
            for(LL k=0;k<=n;k++)
                tmp.m[i][j]=(tmp.m[i][j]+a.m[i][k]*b.m[k][j]%mod)%mod;
    return tmp;
}
void pw(LL m,LL n)//矩阵快速幂
{
	for(LL i=0;i<=n;i++)
		for(LL j=0;j<=n;j++)
			res.m[i][j]=ans.m[i][j];
	while(m!=0)
	{
		if(m&1==1) ans=mul(ans,res,n);
		res=mul(res,res,n);
		m>>=1;
		}
}
int main()
{
    LL k,m,n;
    scanf("%lld%lld%lld",&k,&m,&n);
	buildmatrix(k);
    for(LL i=1;i<=m;i++)//储存操作至A
    {
        LL x,y,z;
        scanf("%lld",&x);
        if(x==1)
        {
            scanf("%lld",&y); 
            bas1.m[y][0]=1;
            ans=mul(bas1,ans,k);
            bas1.m[y][0]=0;
            }
        else if(x==2)
        {
            scanf("%lld%lld",&y,&z);
            bas2.m[y][y]=0; bas2.m[z][y]=1;
            ans=mul(bas2,ans,k);
            bas2.m[y][y]=1; bas2.m[z][y]=0;
            }
        else if(x==3)
		{
			scanf("%lld",&y);
			bas3.m[y][y]=2;
			ans=mul(bas3,ans,k);
			bas3.m[y][y]=1;
			}
    }
	pw(n-1,k);
	pig.m[0][0]=1;
	ans=mul(ans,pig,k);//得到最终矩阵
	for(int i=1;i<=k;i++)
		printf("%lld ",ans.m[i][0]);
	return 0;
}