python3的主成分分析实现
1 主成分分析
主成分分析是最常用的线性降维方法,他的目标是通过某种线性投影,将高维的数据映射到低维的空间中,并期望在所投影的维度上数据的方差最大,以此使用较少的维度,保留原样本数据,并进行一定的分类效果。
2 代码
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# 类别1
mean_vec1 = np.zeros(3)
cov_vec1 = np.eye(3)
class1_sample = np.random.multivariate_normal(mean_vec1, cov_vec1, 20)
# 类别2
mean_vec2 = np.ones(3)
cov_vec2 = np.eye(3)
class2_sample = np.random.multivariate_normal(mean_vec2, cov_vec2, 20)
# 三维数据显示
fig = plt.figure()
ax3d = Axes3D(fig)
ax3d.scatter(class1_sample[:, 0], class1_sample[:, 1], class1_sample[:, -1], c='red', marker='*')
ax3d.scatter(class2_sample[:, 0], class2_sample[:, 1], class2_sample[:, -1], c='green', marker='v')
ax3d.set_xlabel('x')
ax3d.set_ylabel('y')
ax3d.set_zlabel('z')
plt.show()
# 样本融合
all_samples = np.concatenate((class1_sample.T, class2_sample.T), axis=1)
# 特征属性的平均值
mean_x = np.mean(all_samples[0, :])
mean_y = np.mean(all_samples[1, :])
mean_z = np.mean(all_samples[-1, :])
# 平均向量
mean_vector = [[mean_x], [mean_y], [mean_z]]
# 计算散布矩阵
scatter_matrix = np.zeros((3, 3))
for i in range(all_samples.shape[1]):
scatter_matrix += (all_samples[:, i].reshape(3, 1) - mean_vector).dot(
(all_samples[:, i].reshape(3, 1) - mean_vector).T)
# 计算散布矩阵的特征值与特征向量
cov_val, cov_vec = np.linalg.eig(scatter_matrix)
# 特征向量矩阵
p_matrix = cov_vec[:-1, :]
# 原样本转换为2维空间
sample1 = class1_sample.dot(p_matrix.T)
sample2 = class2_sample.dot(p_matrix.T)
# 二维分类结果
plt.scatter(sample1[:, 0], sample1[:, -1], c='red', marker='*')
plt.scatter(sample2[:, 0], sample2[:, -1], c='green', marker='v')
plt.show()
3 代码分析
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
%matplotlib inline
# 创建数据类别1
mean_vec1 = np.zeros(3)
cov_vec1 = np.eye(3)
class1_sample = np.random.multivariate_normal(mean_vec1, cov_vec1, 20)
# 创建数据类别2
mean_vec2 = np.ones(3)
cov_vec2 = np.eye(3)
class2_sample = np.random.multivariate_normal(mean_vec2, cov_vec2, 20)
##数据一
[[-0.18824646 -1.33075096 -0.50953962] [-1.51345505 -0.21800559 -0.19354508] [ 0.06972766 1.28399446 -0.70890196] [-1.51182542 0.45581198 1.66305495] [ 0.50393135 1.08821783 0.79799525] [ 0.57135366 1.61395242 0.55793326] [ 1.02407165 -1.41778723 -0.36826073] [ 1.98043694 -0.08672202 -0.97120255] [-1.23079047 1.34163702 -1.24938097] [ 0.9335483 0.44425385 0.27977026] [-0.72184862 -0.49866148 -1.56652308] [ 1.13328421 0.31036248 -1.45290437] [ 1.0157016 -1.32093825 -1.09136048] [ 1.52518567 1.59195416 -1.38433345] [ 0.38703136 0.92409533 1.45326261] [ 0.59927004 -0.59666334 0.17839374] [-0.66518415 -1.43809813 1.09350578] [-1.46955758 0.18001336 -0.76495692] [-0.72943385 0.71111324 -1.02510776] [-0.3507752 0.31299407 -0.19680486]]
##数据二
[[ 1.33769733 0.28473144 -0.04875153] [ 1.58317734 0.62258189 -1.38034385] [-0.79252804 1.17062301 1.4898586 ] [ 1.2243252 1.28736916 0.87256069] [ 0.70472781 1.8335202 1.7392653 ] [-1.27203079 0.19023692 1.91827356] [ 1.84398833 1.77172076 1.10738029] [ 0.96184992 2.16924159 -1.16572662] [ 2.09161784 2.80988672 0.82252391] [ 0.45899857 0.9931214 0.45920956] [ 0.61343236 1.61840536 -0.64902815] [ 0.4456511 0.62043124 1.16013802] [ 0.83416574 0.99955764 -0.08979452] [ 0.26529412 2.43121433 0.5488105 ] [ 1.59844842 0.96479399 1.53844923] [ 1.23519874 -0.71355965 -0.65513125] [ 0.89733245 1.11660151 1.50145115] [ 1.10857813 2.31673053 0.94663564] [ 1.76717208 1.32904038 2.27194158] [ 1.35635691 4.17526895 0.73188424]]
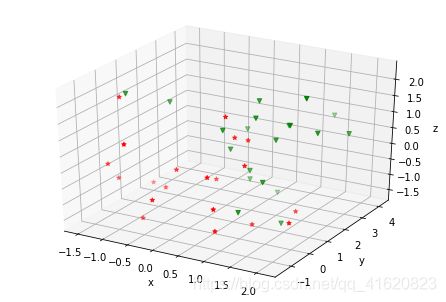
# 在三维空间展示数据
fig=plt.figure()
ax3d=Axes3D(fig)
ax3d.scatter(class1_sample[:,0],class1_sample[:,1],class1_sample[:,-1],c='red',marker='*')
ax3d.scatter(class2_sample[:,0],class2_sample[:,1],class2_sample[:,-1],c='green',marker='v')
ax3d.set_xlabel('x')
ax3d.set_ylabel('y')
ax3d.set_zlabel('z')
plt.show()
可以明显看到两组数据在三维空间的位置,具有严格的不可分性;
#将两组数据组合起来(横向组合)
all_samples=np.concatenate((class1_sample.T,class2_sample.T),axis=1)
##组合的数据
[[-0.18824646 -1.51345505 0.06972766 -1.51182542 0.50393135 0.57135366 1.02407165 1.98043694 -1.23079047 0.9335483 -0.72184862 1.13328421 1.0157016 1.52518567 0.38703136 0.59927004 -0.66518415 -1.46955758 -0.72943385 -0.3507752 1.33769733 1.58317734 -0.79252804 1.2243252 0.70472781 -1.27203079 1.84398833 0.96184992 2.09161784 0.45899857 0.61343236 0.4456511 0.83416574 0.26529412 1.59844842 1.23519874 0.89733245 1.10857813 1.76717208 1.35635691] [-1.33075096 -0.21800559 1.28399446 0.45581198 1.08821783 1.61395242 -1.41778723 -0.08672202 1.34163702 0.44425385 -0.49866148 0.31036248 -1.32093825 1.59195416 0.92409533 -0.59666334 -1.43809813 0.18001336 0.71111324 0.31299407 0.28473144 0.62258189 1.17062301 1.28736916 1.8335202 0.19023692 1.77172076 2.16924159 2.80988672 0.9931214 1.61840536 0.62043124 0.99955764 2.43121433 0.96479399 -0.71355965 1.11660151 2.31673053 1.32904038 4.17526895] [-0.50953962 -0.19354508 -0.70890196 1.66305495 0.79799525 0.55793326 -0.36826073 -0.97120255 -1.24938097 0.27977026 -1.56652308 -1.45290437 -1.09136048 -1.38433345 1.45326261 0.17839374 1.09350578 -0.76495692 -1.02510776 -0.19680486 -0.04875153 -1.38034385 1.4898586 0.87256069 1.7392653 1.91827356 1.10738029 -1.16572662 0.82252391 0.45920956 -0.64902815 1.16013802 -0.08979452 0.5488105 1.53844923 -0.65513125 1.50145115 0.94663564 2.27194158 0.73188424]]
#计算每个维度的平均值,并组合为向量
mean_x=np.mean(all_samples[0,:])
mean_y=np.mean(all_samples[1,:])
mean_z=np.mean(all_samples[-1,:])
mean_vector=[[mean_x],[mean_y],[mean_z]]
#计算散布矩阵
scatter_matrix=np.zeros((3,3))
for i in range(all_samples.shape[1]):
scatter_matrix+=(all_samples[:,i].reshape(3,1)-mean_vector).dot((all_samples[:,i].reshape(3,1)-mean_vector).T)
##散布矩阵
[[58.47880319 5.25865694 6.97297876] [ 5.25865694 29.32284753 12.84701742] [ 6.97297876 12.84701742 54.36874878]]
##计算特征值和特征向量
cov_val,cov_vec=np.linalg.eig(scatter_matrix)
##特征值
[67.67454409 50.73021281 23.7656426 ]
##特征向量
[[ 0.68120972 0.72918572 0.06512683] [ 0.31480819 -0.21145288 -0.92530183] [ 0.66094563 -0.65082706 0.37359739]]
## 取前2维特征向量组成特征向量矩阵(按照特征值从大到小排列)
p_matrix=cov_vec[:-1,:]
##原样本转换为2维空间
sample1=class1_sample.dot(p_matrix.T)
sample2=class2_sample.dot(p_matrix.T)
#二维分类结果
plt.scatter(sample1[:,0],sample1[:,-1],c='red',marker='*')
plt.scatter(sample2[:,0],sample2[:,-1],c='green',marker='v')