树上差分（点差分与边差分）

矩阵的差分应该很简单，典型题目是这样的：

给你一堆数，有n次修改操作，每次给i..j这个区间加上x。最后问所有数中最大的那个。

差分，通俗一点就是把区间的操作改为点操作，在点上记录变化量。上题只需记录dlt[i]+=x,dlt[j+1]-=x，最后用前缀和扫一遍即可。

树上差分，顾名思义就是在树上搞差分。

有两种典型题型，一种是边差分，一种是点差分。

边差分

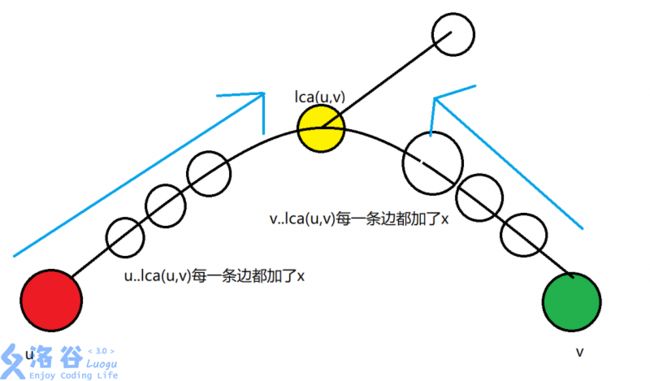
给你一棵树，有n次修改操作，每次把u..v的路径权值加x，最后问从x..y的路径权值和。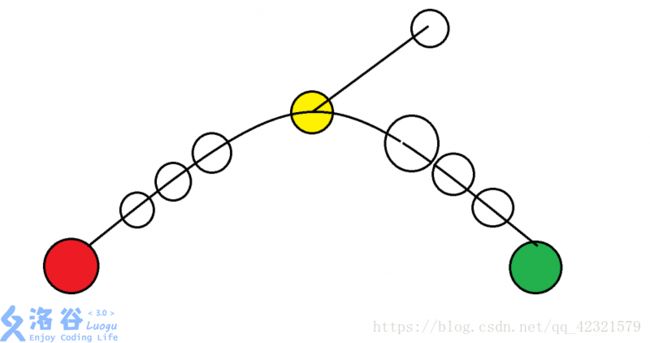

 

 

例如有一次操作是把红点（u）到绿点（v）之间的路径全部加x。那么我就标记dlt[u]+=x,dlt[v]+=x。

这样在最后求解的时候，回溯的时候顺便算一下答案就出来了。

然后我们要在lca(u,v)处标记dlt[lca(u,v)]-=2x。这样就使得加x的效果只局限在u..v，不会向lca(u,v)的爸爸蔓延。

点差分

点差分和边差分稍有差别：

有n次修改操作，每次把u..v的所有点权都加x，最后问点权最大的为多少。

做法也是和边差分稍有不同，我们不在dlt[lca(u,v)]-=2x，而是把dlt[lca(u,v)]-=x并把dlt[fa[lca(u,v)]]-=x。为什么呢？因为lca(u,v)也在u..v这条路径上，它同样需要被加x。回溯的时候会从u和v两个方向都给lca(u,v)加一个x，而它只能加一个，因此dlt[lca(u,v)]-=x。而lca(u,v)的爸爸则根本无法被加，在lca(u,v)已经只加一个x了，因此dlt[fa[lca(u,v)]]-=x就能让lca(u,v)的爸爸不加x。

点差分例题：[USACO15DEC]最大流Max Flow

直接上代码：

#include
#include
#include
#include
#include
using namespace std;
int max0;//指数大小 
vector vec[50005]; 
int fa[50005][20], dep[50005],dlt[50005]; 
int ans = 0; 
void dfs(int x){
    for(int i = 1;i <= max0;i++){
        fa[x][i]=fa[fa[x][i-1]][i-1];//i的第2^j个父亲 是i的第2^(j-1)个父亲的第2^(j-1)个父亲
    } 
    for(int i = 0; i < vec[x].size();i++){
    	int u = vec[x][i];
        if(u != fa[x][0]){     //如果u不是x的父亲就是x的儿子
            fa[u][0] = x;       //记录儿子的第一个父亲是x
            dep[u] = dep[x] + 1;      //处理深度
            dfs(u);
        }
    }
}
int LCA(int u,int v){
    if(dep[u] < dep[v]) swap(u,v);  //我们默认u的深度一开始大于v，那么如果u的深度小就交换u和v
    int delta = dep[u] - dep[v];    //计算深度差
    for(int x = 0;x <= max0;x++){    //此循环用于提到深度相同。x从0或者max0开始都可以 
        if((1 << x) & delta)//因为我们要将u往上提delta个深度，所以将delta分解成二进制后，找到是1的位就向上提2^x个深度，这样最后一定提了delta个位 
            u = fa[u][x];
    }
    if(u == v) return u;//深度相同而且相等，表示原来u、v就在一条树链上，直接返回此时的结果 
    for(int x = max0;x >= 0;x--)     //注意！此处循环必须是从大到小!因为我们应该越提越“精确”，
        if(fa[u][x] != fa[v][x]){   //如果从小到大的话就有可能无法提到正确位置，自己可以多想一下
			u = fa[u][x];
            v = fa[v][x];
        }
    return fa[u][0];    //此时u、v的第一个父亲就是LCA。
}
void dfs_cnt(int x){//回溯前缀和，找到最大的点权 
	for(int i = 0; i < vec[x].size(); i++){
		int v = vec[x][i];
		if(v != fa[x][0]){
			dfs_cnt(v);
			dlt[x] += dlt[v];
		}
		ans = max(ans, dlt[x]);
	}
}
int main(){
	int n,k;
	cin >> n >> k;
	max0 = log2(n);
	for(int i = 0; i < n - 1; i++){
		int a,b;
		scanf("%d%d",&a,&b);
		vec[a].push_back(b);
		vec[b].push_back(a);
	}
	dfs(1);
	for(int j = 0; j < k; j++){
		int a,b;
		scanf("%d%d",&a,&b);
		int c = LCA(a,b);
		dlt[c]--,dlt[fa[c][0]]--;//树上的点差分 
		dlt[a]++,dlt[b]++;
	}
	dfs_cnt(1); 
	cout << ans << endl;
	return 0;
} 

差分适用于修改多而询问少的情况，本题中只有一次询问，非常适合，又学习了一种数据结构，棒棒~~