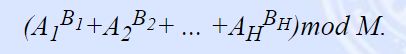SZU寒训day1
SZU寒训day1
introduction
day1的主要内容是贪心、二分、三分、快速幂。本文纯属做个回顾。
贪心
贪心就是用当前最优来替代整体最优啦。但是不是所有地方都可以这么用,要自行证明当前最优时整体解必然最优。
二分
二分查找
时间复杂度:O(logn) 当然很多时候还需要一个O(nlogn)的快排
二分答案
用于答案有一定范围?验证答案的函数是单调的?(比如求minimax或maximin)
时间复杂度:O(k*nlogn)(k是验证答案的时间)
emmm…基本上弱爆了吧
三分
上面说了二分是在单调函数里找某个值,那三分就是在凹函数或者凸函数里面找极值 首先来看看求 a b a^b ab的一般写法。 但当要求b超级无敌大的时候,这种三行的代码就显得那么的苍白无力,于是在二进制的启发下有了快速幂。 原理 balabala完了看题 给你一堆电视节目开始结束时间,输出能完整看到的电视节目的个数。 也就是求没有交集的最多区间,冥冥中有种贪心的感觉。 按结束时间排序 O(nlogn) 给定自然数l和r ,选取2个整数x,y满足l <= x <= y <= r ,使得x|y最大。 要研究一下或运算,有1则1,零零得0。 当[l,r)中没有 2 k − 1 2^k-1 2k−1时,也就是说l跟r二进制下位数相同,那l跟r的二进制形式肯定有左t位相同,第t+1位,r为1,l为0。[l,r]中所有数前t位都会相同,由于|的结果有1则1,r第t+1位为1,|后第t+1位也是1.所以我们只要让y从t+2位开始都是1,而前t+1位与l相同就行。r|y就是答案。(为什么y∈[l,r]呢?) 我有n个大小不一的蛋糕,f+1个人分,每个人只吃一块the same size的蛋糕。问最多每个人能吃多少? 乍一看就想平均分了,但是不行,人家宁愿扔了剩下的,也只吃从一个蛋糕上来的一块。好像直接没法求一个人能吃多少。但是要是告诉我每个人吃了多少,我可以求出蛋糕够不够吃。 二分答案,范围(0,maxpiesize],但是这一题卡精度卡得十分难受。 如图,已知H,h,D,求max(L) 搞出他的函数出来,发现是凸函数。 三分 由于数很大,所以要用以下公式 快速幂 F(x) = max(Si(x)), i = 1 . . . n. The domain of x is [0, 1000]. Si(x) is a quadric function. 画画图就知道F(x)是凹函数,于是就可以三分啦。 有N个人口不一的城市要选举,Mac做了M个投票箱。求他制作投票箱的容量最少是多少,才能让每个城市每个人都可以投票。 跟上面分蛋糕差不多,直接好像没法求。那就逆向思维,猜一个投票箱容量,验证一下行不行。 二分 给出p,a两个数,问p是不是关于a的伪素数(即不是素数但符合费马小定理) 费马小定理 emmm~什么东西?别管,按题目模拟就完事儿。 快速幂+判素数 A为一个方阵,则Tr A表示A的迹(就是主对角线上各项的和),求Tr(A^k)%9973。 矩阵快速幂裸题 第一天水题为主。
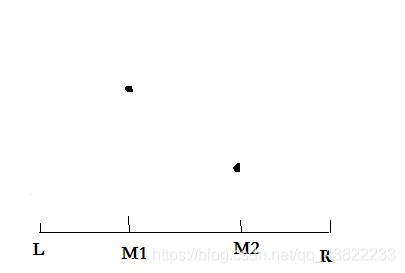
若f(x)是凸函数,f(M1)>f(M2)时,R取M2,f(M1)快速幂
ans=1;
for(int i=0;i<b;i++)
ans*=a;
首先先看一个例子。求 3 8 3^8 38怎么做才会快呢?
先拆成乘法,看看有哪些重复运算,把他去掉。
ans=3 * 3 * 3 * 3 * 3 * 3 * 3 * 3 显然这里 3 ∗ 3 3*3 3∗3是一个重复运算,我们算一次 3 ∗ 3 = 9 3*3=9 3∗3=9代进去就好
ans=9 * 9 * 9 * 9 显然这里 9 ∗ 9 9 * 9 9∗9是重复运算,我们算一次 9 ∗ 9 = 81 9 * 9=81 9∗9=81代进去就好
ans=81 * 81=6561
这样我们用了3次乘法就解决了本来8次乘法的问题了。
废话就说到这了
上代码ans=1;
while(b)
{
if(b&1)ans=ans*a;//b&1等价于b%2
b>>=1;//右移1位,等价于b/=2
a=a*a;
}
把b化为二进制数,如果是奇数就证明有一个单独的a不能做重复乘法,所以就把它乘了。于是剩下的a是偶数个,可以化为 ( a 2 ) (a^2) (a2)^(b/2),此时a*a要重复b遍。所以干脆a=a * a,b/=2,于是就可以变成 a b a^b ab,发现没有,又是 a b a^b ab。于是就是递归啦!HDU 2037
题意
分析
贪啥呢?贪结束时间,先看结束时间早的(让影响后面的节目最少),然后找这个节目结束后开始的结束时间最早的,循环~解
遍历一边 O(n)
总时间复杂度 O(nlogn)HDU - 5969
题意
其中|表示按位或。分析
一开始我的想法是让x=r,让y为[l,r)中最大一个 2 k − 1 2^k-1 2k−1,这样y在二进制下就是比r小一位,每位都是1的数,那x|y=2^(k+1)-1显然是最大的。但很快我就发现了一个问题,要是[l,r)中没有 2 k − 1 2^k-1 2k−1怎么办,显然我的答案只是特殊情况。解
其实当[l,r)中有 2 k − 1 2^k-1 2k−1时,这个 2 k − 1 2^k-1 2k−1也是上面所说y的特殊情况。代码
#includeHDU - 1969
题意
分析
解
代码
#includeZOJ - 3203
题意
分析
解
代码
#includePOJ - 1995
题意
分析
ab%m=(a%m)(b%m)%m
(a+b)%m=a%m+b%m解
代码
#includeUVALive - 5009
题意
求the minimum of F(x)(x∈[0,1000])分析
求f(x)要算一次n个函数,求最大值。代码
#includeHRBUST - 2176
题意
分析
解
代码
#includePOJ 3641
题意
分析
解
注意要开long long代码
#includeHDU - 1575
题意
分析
代码
#include最后
由于本蒟蒻水平有限,本文仅供参考。(有错轻喷 )