A - Alice的难题（数论+前后缀预处理）

传送门

---

1.第一步肯定是求出所有数的鸡汤值了，考虑到最小质因子，使用欧拉筛即可求得（不懂自行百度）

2.对于三个不相交的连续区间$a,b,c$，如下所示：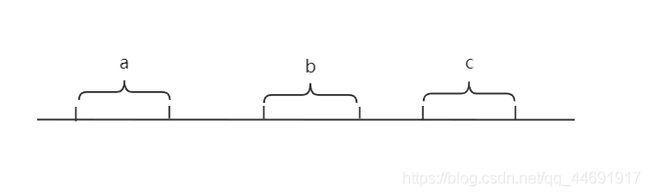
我们可以发现对应排列有以下六种情况：

• $a,b,c$
• $a,c,b$
• $b,a,c$
• $b,c,a$
• $c,a,b$
• $c,b,a$

3.对于上面的每种情况，我们设从左向右分别是$x,y,z$。不难想到我们需要在区间$[x,n-z]$内枚举所有长度为$y$的线段，问题便转化为，求区间$[1,n-y-z]$内每个前缀的长度为$x$的最大区间；求区间$[x+y+1,n]$内的每个后缀的长度为$z$的最大区间。那么我们只需预处理前缀后缀，然后预处理长度为$x$的区间右端点结束的最大值，长度为$z$的区间左端点起始的最大值。这样之后在枚举$y$，就很容易求出答案了

#include <set>
#include <map>
#include <stack>
#include <queue>
#include <math.h>
#include <cstdio>
#include <string>
#include <bitset>
#include <cstring>
#include <sstream>
#include <iostream>
#include <algorithm>
#include <unordered_map>
using namespace std;
#define fi first
#define se second
#define pb push_back
#define ins insert
#define lowbit(x) (x&(-x))
#define mkp(x,y) make_pair(x,y)
#define mem(a,x) memset(a,x,sizeof a);
typedef long long ll;
typedef long double ld;
typedef unsigned long long ull;
typedef pair<int,int> P;
const double eps=1e-8;
const double pi=acos(-1.0);
const int inf=0x3f3f3f3f;
const ll INF=1e18;
const int Mod=1e9+7;
const int maxn=1e6+10;

int prime[maxn/3],num[maxn],fac[maxn];
ll pre[maxn],sub[maxn];
ll L[maxn],R[maxn];
int cnt,n;

void euler() {
    int tmp;
    for(int i=2;i<maxn;i++){
        if(!fac[i]){
            prime[cnt++]=i;
            fac[i]=i;
        }
        for(int j=0;(tmp=i*prime[j])<maxn;j++){
            fac[tmp]=prime[j];
            if(!(i%prime[j])) break;
        }
    }
}

ll solve(int x,int y,int z){
    int m1=n-y-z,m2=x+y+1;
    ll res=0;
    for(int i=1;i+x-1<=m1;i++){
        res=max(res,pre[i+x-1]-pre[i-1]);
        L[i+x-1]=res;
    }
    res=0;
    for(int i=n;i-z+1>=m2;i--){
        res=max(res,sub[i-z+1]-sub[i+1]);
        R[i-z+1]=res;
    }
    ll ans=0;
    for(int i=x;i+y<=n-z;i++){
        ans=max(ans,pre[i+y]-pre[i]+L[i]+R[i+y+1]);
    }
    return ans;
}

int main(){
    //freopen("in.txt","r",stdin);
    //freopen("out.txt","w",stdout);
    //ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    int t,a,b,c;
    scanf("%d",&t);
    euler();
    while(t--){
        scanf("%d",&n);
        scanf("%d%d%d",&a,&b,&c);
        for(int i=1,x;i<=n;i++){
            scanf("%d",&x);
            num[i]=fac[x];
        }
        pre[0]=sub[n+1]=0;
        for(int i=1;i<=n;i++) pre[i]=pre[i-1]+num[i];
        for(int i=n;i>=1;i--) sub[i]=sub[i+1]+num[i];
        ll ans=0;
        ans=max(ans,solve(a,b,c));
        ans=max(ans,solve(a,c,b));
        ans=max(ans,solve(b,a,c));
        ans=max(ans,solve(b,c,a));
        ans=max(ans,solve(c,a,b));
        ans=max(ans,solve(c,b,a));
        printf("%lld\n",ans);
    }
    return 0;
}