Ural 1519 Formula 1
1519. Formula 1
Memory Limit: 16 MB
Background
Regardless of the fact, that Vologda could not get rights to hold the Winter Olympic games of 20**, it is well-known, that the city will conduct one of the Formula 1 events. Surely, for such an important thing a new race circuit should be built as well as hotels, restaurants, international airport - everything for Formula 1 fans, who will flood the city soon. But when all the hotels and a half of the restaurants were built, it appeared, that at the site for the future circuit a lot of gophers lived in their holes. Since we like animals very much, ecologists will never allow to build the race circuit over the holes. So now the mayor is sitting sadly in his office and looking at the map of the circuit with all the holes plotted on it.
Problem
Who will be smart enough to draw a plan of the circuit and keep the city from inevitable disgrace? Of course, only true professionals - battle-hardened programmers from the first team of local technical university!.. But our heroes were not looking for easy life and set much more difficult problem: "Certainly, our mayor will be glad, if we find how many ways of building the circuit are there!" - they said.
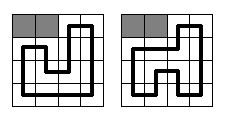
It should be said, that the circuit in Vologda is going to be rather simple. It will be a rectangle N*M cells in size with a single circuit segment built through each cell. Each segment should be parallel to one of rectangle's sides, so only right-angled bends may be on the circuit. At the picture below two samples are given for N = M = 4 (gray squares mean gopher holes, and the bold black line means the race circuit). There are no other ways to build the circuit here.
Input
The first line contains the integer numbers N and M (2 ≤ N, M ≤ 12). Each of the next N lines contains M characters, which are the corresponding cells of the rectangle. Character "." (full stop) means a cell, where a segment of the race circuit should be built, and character "*" (asterisk) - a cell, where a gopher hole is located.
Output
You should output the desired number of ways. It is guaranteed, that it does not exceed 263-1.
Samples
| input |
output |
|---|---|
| 4 4**.............. |
2 |
| 4 4................ |
6 |
| 3814039 | 12:33:28 27 Sep 2011 |
= Dwylkz = | 1519. Formula 1 | C++ | Accepted | 0.218 | 1 392 KB |
It's the frist time, i solve Pulg_DP problem and AC in Ural. To my surprise, Ural's URL dosen't have any word which has "Ural" inside. Finally, i find out that Ural is a school in Russa.
Pulg_DP, it sounds like something difficult. But unfortunately, nowadays, most of the time, it will appear in ACM, like segment tree. So, i have to spend few days on it..
Pulg_DP is a kind of State compressed DP, but it depended on Conectivty, u can find some detail in Chen dan qi's PPT.
Actually, the time i spend on coding hash table is longer than comprehand Plug_DP theory. The hash table is an important point, because it seriously affects ur program's efficiency.
It's easy to conclude the range of the state is 0 ~ 3 ^ 13 and as Bit operation is faster, i use quatenary instead. Of course it will MLE if we define a hash array with 4 ^ 13 elements. According to the exactly number of state, I define a simply hash funtion which is based on module operation and use link list to avoid the conflict in mapping.
The following is my ugly code and the my English is ugly too{= =}.
#include
#include
#include
#include
using namespace std;
#define MAXN (13)
#define MAXSS (531441)
#define MAXS (4151)
#define LLU __int64
#define L(x) (1 << x)
#define R(x) ((1 << x) << 1)
#define LR(x, y) ((1 << x) << (y - 1))
#define GET(x, y) ((x >> y) & 3)
char M[MAXN][MAXN];
int t, n, m, ei, ej;
struct State
{
LLU s, c;
} ts;
vector S[2];
struct Hash
{
vector hash[MAXS];
void clr()
{
int i;
for (i = 0; i < MAXS; i++)
hash[i].clear();
}
void ins(LLU x, LLU add)
{
LLU key = x % MAXS;
int i;
for (i = 0; i < hash[key].size(); i++)
if (S[!t][hash[key][i]].s == x)
break;
if (i == hash[key].size())
{
hash[key].push_back(S[!t].size());
S[!t].push_back(ts);
}
else S[!t][hash[key][i]].c += add;
}
} H;
LLU find(LLU s, LLU i, bool np)
{
int b = 1, p = 2, d = 1;
if (np) swap(p, d);
while (b)
{
if (np) i += 2;
else i -= 2;
if (GET(s, i) == p) b++;
if (GET(s, i) == d) b--;
}
return i;
}
LLU SCDP()
{
LLU l, u, li, ui, b, res = 0;
int i, j, k;
t = 0;
ts.s = 0;
ts.c = 1;
S[0].clear();
S[0].push_back(ts);
for (i = 0; i < n; i++)
{
li = 0; ui = 2;
for (j = 0; j < m; j++)
{
H.clr();
S[!t].clear();
for (k = 0; k < S[t].size(); k++)
{
ts = S[t][k];
l = GET(ts.s, li);
u = GET(ts.s, ui);
if (!M[i][j])
{
if (!l && !u) H.ins(ts.s, ts.c);
}
else
{
if (!l && !u)
{
if (i + 1 < n && j + 1 < m && M[i + 1][j] && M[i][j + 1]) //## -> ()
{
ts.s += L(li) + R(ui);
H.ins(ts.s, ts.c);
}
}
else if (!l || !u)
{
if (l && !u)
{
if (i + 1 < n && M[i + 1][j]) //*# -> *#
{
H.ins(ts.s, ts.c);
}
if (j + 1 < m && M[i][j + 1]) //*# -> #*
{
ts.s += LR(ui, l) - LR(li, l);
H.ins(ts.s, ts.c);
}
}
else if (!l && u)
{
if (j + 1 < m && M[i][j + 1]) //#* -> #*
{
H.ins(ts.s, ts.c);
}
if (i + 1 < n && M[i + 1][j]) //#* -> *#
{
ts.s += LR(li, u) - LR(ui, u);
H.ins(ts.s, ts.c);
}
}
}
else if (l && u)
{
if (l == 1 && u == 2) // () -> ##
{
if (i == ei && j == ej)
res += ts.c;
}
else
{
if (l == 1 && u == 1) //(( -> ##
{
b = find(ts.s, ui, true);
ts.s += L(b) - R(b) - L(li) - L(ui);
}
else if (l == 2 && u == 2) //)) -> ##
{
b = find(ts.s, li, false);
ts.s += R(b) - L(b) - R(li) - R(ui);
}
else if (l == 2 && u == 1) //)( -> ##
{
ts.s -= R(li) + L(ui);
}
H.ins(ts.s, ts.c);
}
}
}
}//K end.
t ^= 1;
li += 2; ui += 2;
}//J end.
for (j = 0; j < S[t].size(); j++)
S[t][j].s <<= 2;
}//I end.
return res;
}
int main()
{
#ifndef ONLINE_JUDGE
freopen("test.txt", "rt", stdin);
#endif
int i, j;
while (~scanf("%d%d", &n, &m))
{
for (i = 0; i < n; i++)
scanf("%s", M[i]);
for (i = 0; i < n; i++)
for (j = 0; j < m; j++)
if (M[i][j] == '.')
{
M[i][j] = true;
ei = i;
ej = j;
}
else M[i][j] = false;
printf("%I64d\n", SCDP());
//break;
}
return 0;
}
Besides, Timus only support __int64.
That's it, have a good coding time~{= =}