【Codeforces Round #632 (Div. 2) / 1333C】- C. Eugene and an array - 思维 + 计数（详解）

C. Eugene and an array

time limit per test ：1.5 seconds                                 memory limit per test ：256 megabytes
inputstandard input                                        outputstandard output

Eugene likes working with arrays. And today he needs your help in solving one challenging task.

An array c is a subarray of an array b if c can be obtained from b by deletion of several (possibly, zero or all) elements from the beginning and several (possibly, zero or all) elements from the end.

Let's call a nonempty array good if for every nonempty subarray of this array, sum of the elements of this subarray is nonzero. For example, array [−1,2,−3] is good, as all arrays [−1], [−1,2], [−1,2,−3], [2], [2,−3], [−3] have nonzero sums of elements. However, array [−1,2,−1,−3] isn't good, as his subarray [−1,2,−1] has sum of elements equal to 0.

Help Eugene to calculate the number of nonempty good subarrays of a given array a.

Input

The first line of the input contains a single integer n (1≤n≤2×105)  — the length of array a.

The second line of the input contains n integers a1,a2,…,an (−109≤ai≤109)  — the elements of a.

Output

Output a single integer  — the number of good subarrays of a.

Examples

input

3
1 2 -3

output

5

input

3
41 -41 41

output

3

Note

In the first sample, the following subarrays are good: [1], [1,2], [2], [2,−3], [−3]. However, the subarray [1,2,−3] isn't good, as its subarray [1,2,−3] has sum of elements equal to 0.

In the second sample, three subarrays of size 1 are the only good subarrays. At the same time, the subarray [41,−41,41] isn't good, as its subarray [41,−41] has sum of elements equal to 0.

题目大意

给一个长度为n的数组a，问有多少子串满足没有和为0的子串？

思路

这个是一个计数题，对于计数题我们要做到不重不漏，一开始我是前缀和然后排序再处理，完全跑偏（不能排序，但是我一直没发现），不管怎么做都会算重或算漏。

1. 如何知道一个串和是否为0？我们只要用map记录是否出现过这个sum值，如果一个sum值在之前出现过，现在又出现，那么从之前的位置到现在的位置这个子串的和就为0。
2. 对于一个串我们可以很快知道有多少串包含这个串，但是一个串可以包含多个串，有的串和为0，有的串和不为0，这是造成重复统计的原因，那么一个和为0的串我们要如何计算不包含当前串和其他和为0的串且还未被统计的串呢？我们只要枚举右端点然后统计有多少合法的左端点，以当前点为右端点就可以保证所计算的串在这之前未被统计过，来看下面这张图。
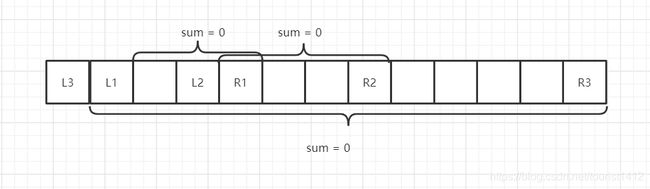
3. 当我们统计到R3这个位置时，我们可以发现从L3 + 2 ~ R3 - 1之间的任意一点作为左端点都不包含串（L3，R3]，但是可能会包含串(L1, R1]，(L2, R2]，L2 + 1 ~ R3 - 1之间的点才是合法的左端点（L2为L1，L2，L3中最大的左端点）。我们可以用map记录sum上一次出现的位置（即左端点）。
4. 也就是说我们要用一个变量pre记录sum = 0的串的左端点的最大值，以保证不包含sum = 0的串。（pre要初始化为-1，因为我们表示串的方式是左开右闭）
5. 代码实现起来很短，但要注意map的使用，因为我们初始pos[0] = 0(pos是一个map），在下次遇到sum = 0时判断语句if (pos[sum])会出现问题，所以用if( pos.count(sum))来判断sum是否出现过。

代码

#include 
using namespace std;
#define pb push_back
#define mp make_pair
#define fi first
#define se second
typedef long long ll;
typedef unsigned long long ull;
typedef pair PII;
const int mod = 1e9 + 7;
const int N = 2e5 + 10;
const int INF = 0x3f3f3f3f;
ll qpow(ll base, ll n){ll ans = 1; while (n){if (n & 1) ans = ans * base % mod; base = base * base % mod; n >>= 1;} return ans;}
ll gcd(ll a, ll b){return b ? gcd(b, a % b) : a;}
map pos;
int main()
{
	int n;
	cin >> n;
	ll tmp, sum = 0, ans = 0;
	pos[0] = 0;
	int pre = -1;
	for (int i = 1; i <= n; ++ i){
		scanf("%lld", &tmp);
		sum += tmp;
		if (pos.count(sum))pre = max(pre, pos[sum]);
		ans += i - pre - 1;
		pos[sum] = i;
	}
	cout << ans << endl;
	return 0;
}