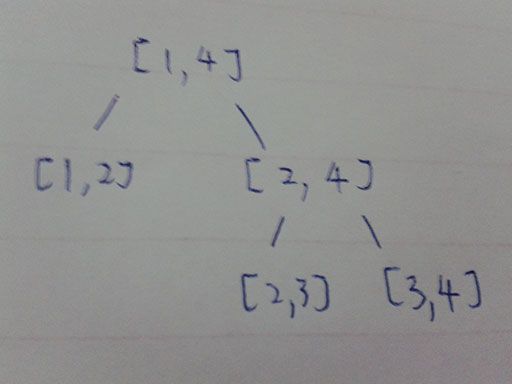扫描线用于求若干个相交矩形的面积并,因为用几何方法在相交的情况复杂的时候难以计算。下面给2个矩形的情况做例子
给定2个矩形对角的点坐标,则下图的面积为图2的三种颜色面积和

图1

图2
现在假设有一条竖着的线从左边往右边扫,扫到矩阵的边时,若是入边,将边这一个区间的cover属性+1,出边则-1
图中圈圈的数字是第几条边,花括号的数是cover值。如图扫描线经过②号边(入边)时最上面部分是1,下面还是1,中间是2,到出边就又减了

图3
则扫描到②号线时,计算一次面积,长为②号线的x减去①号线(前面一条线)的x,高为[Ymin,Ymax]中所有cover为正的高度和
(在这里即为①号线的Yup,Ydown差)。这样重复下去即求得面积和。
放线段树上,区间端点为各条边的上下2个y值,每个区间也都有个cover属性表示覆盖的次数,如上所提。
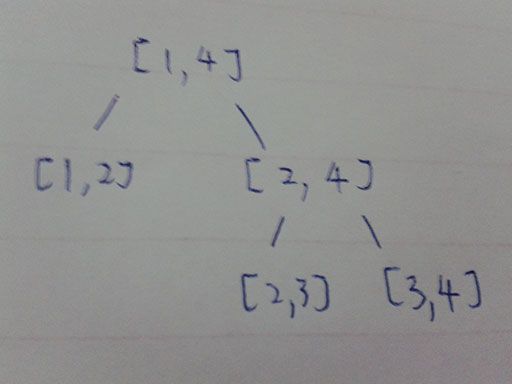
图4
假设点为[1,1],[2,2],[3,3],[4,4](按图1的情况),则有上图。①号线为[1,3],②为[2,4]...
看这图的第二行,前面一个区间是[1,2],后面是[2,4],而不是{3,4],是因为在矩形里,区间是连续的,[2,3]是存在的,如果为mid+1则[2,3]会被弄没。
第三行:[1,2]没有再继续分成[1,1]和[2,2],是因为这样的点区间没有意义,一条线当然要两个点
然而区间端点并不一定是这么好的整数,即可能是浮点数,还可能坐标很大,所以需要对这些区间的Y值离散化(这里不解释,可见),离散化后就跟上图的1,2,3,4一样了。
NEUQ扫描线-视频链接
HDU 1542 Atlantis 也是POJ 1151 Atlantis 不过POJ用G++交的话记得是%.2f而不是%.2lf
思路一:保存区间时区间端点都用double类型,避免离散化的麻烦。然后只对叶区间处理,如扫描图3里的第②条线时,
面积为②号线上cover为1、为2、为1的三段这和。
这种情况下求每一部分面积时:长为当前线的x减去前面一条线的x,代码里的tree[i].x保存上一条线的x值,可以这样做是因为每次求第i条线时,
上一条线已经扫过,在建树时设置x为-1表示没有上一条。
#include
#include
#include
#include
#include
#include
思路二(主流一点):给每个区间增加一个len属性,表示该区间能与下一条线段计算用的高度,然后顺势每次插入线段就用整个大区间(树)与下一条能算的高度求出面积。
(区间存端点有点离散化的思想,把区间存的都变成了常规的整数l,r)如插入②时,因为有y数组排序,插入的区间就是【2,4】,则【2,4】能与下一条计算的是y[4]-y[2],然后通过pushup把【1,2】能计算的也加进来,就可以求②和③中间的面积了。因为区间的l,r是int,所以插入的线段的区间需要用二分在y数组里找出下标。
#include
#include
#include
#include
#include
#include
既然是整型的l,r,那就按常规的线段树飘逸去吧,把tree结构体省了,添加参数代替。
#include
#include
#include
#include
#include
#include