Pytorch学习笔记——卷积神经网络基础

卷积神经网络基础

卷积神经网络包含卷积层、池化层

1、卷积层

二维互相关运算

输入的二维矩阵与一个二维核矩阵的二维互相关计算，通常情况下核矩阵size小于输入矩阵，举例

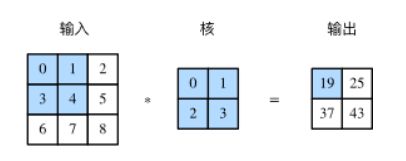
这里实现为0×0+1×1+3×2+4×3=19，然后核矩阵在输入矩阵中向右移动一格，再算1×0+2×1+4×2+5×3=25，以此类推

import torch 
import torch.nn as nn
# corr2d函数实现二维互相关运算，输入矩阵X，核矩阵K，返回输出矩阵Y

def corr2d(X, K):
    H, W = X.shape
    h, w = K.shape
    Y = torch.zeros(H - h + 1, W - w + 1)  # (H-h)/1 + 1 , w  
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            Y[i, j] = (X[i: i + h, j: j + w] * K).sum()    #矩阵对应相乘相加
    return Y

二维卷积层

是输入矩阵与核矩阵的互相关运算加上标量偏置，卷积层用到的并非卷积运算而是互相关运算

# 继承nn.Module父类
class Conv2D(nn.Module):
    # Conv2D(kernel_size)
    def __init__(self, kernel_size):
        super(Conv2D, self).__init__()
        self.weight = nn.Parameter(torch.randn(kernel_size))
        self.bias = nn.Parameter(torch.randn(1))
    # forward(x)
    def forward(self, x):
        return corr2d(x, self.weight) + self.bias   # 二维互相关运算加偏差，广播机制

举例

学习卷积核以检测颜色边缘

X = torch.ones(6, 8)     
Y = torch.zeros(6, 7)
X[:, 2: 6] = 0
Y[:, 1] = 1
Y[:, 5] = -1
print(X)        # size(6,8)
print(Y)        # size(6,7) 列数比特征少一列，0为左到右一列数据不变，1为减1，-1为0减-1，检测图像颜色边缘

conv2d = Conv2D(kernel_size=(1, 2))  # 核size
step = 30
lr = 0.01
for i in range(step): 
    # 求Y_hat
    Y_hat = conv2d(X) # forward(X) 
    l = ((Y_hat - Y) ** 2).sum()
    # l从y_hat反向传播
    l.backward() 
    # 梯度下降
    conv2d.weight.data -= lr * conv2d.weight.grad
    conv2d.bias.data -= lr * conv2d.bias.grad
    
    # 梯度清零
    conv2d.weight.grad.zero_()
    conv2d.bias.grad.zero_()
    if (i + 1) % 5 == 0:
        print('Step %d, loss %.3f' % (i + 1, l.item()))
        
print(conv2d.weight.data)
print(conv2d.bias.data)

2、特征图与感受野

特征图：二维卷积层输出的矩阵被称为输入矩阵某一级别的特征，且特征随着卷积层数量增加而愈发抽象
感受野：输入阴影部分为输出阴影部分的感受野，输入3x3矩阵为输出2x2矩阵的感受野

3、填充和步幅

填充：通常填0，在上下，或者左右填充数字以改变数据矩阵形状

步幅：卷积核在输入数组每次滑动的行数列数，如下为行步幅为2，列步幅为3

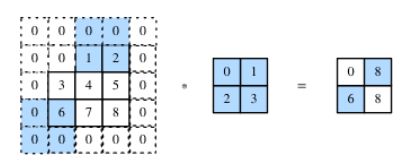
通常情况下，我们可以通过控制填充与步幅的关系来控制输出矩阵形状

其中n，p，k，s分别为行列方向上的输入、填充、核和步幅

4、多输入通道和多输出通道

多输入通道

如RGB图像中输入通道数为3，多输入通道中每一个通道对应一个卷积核，分别做二维互相关运算然后相加得到输出矩阵，可以得知输入size为ci×h×w，卷积核size为ci×kh×kw，输出size与单输入通道与单核做二维互相关计算一致

多输出通道

多输出通道模型如下

若输入层为ci×h×w，输出通道为co，则卷积核size为co×ci×kh×kw，单输出层size与单输入层与单卷积核做二维互相关运算一致

特殊卷积层

1×1卷积层

可以在不改变高和宽的情况下改变通道数

输入输出尺寸相同

我们在卷积神经网络中使用奇数高宽的核，比如 3×3 ， 5×5 的卷积核，对于高度（或宽度）为大小为 2k+1 的核，令步幅为1，在高（或宽）两侧选择大小为 k 的填充，便可保持输入与输出尺寸相同

Pytorch实现卷积层

# 卷积层的实现利用了nn.Conv2d
# 4train_nums, 2 channels, 3 high, 5 wide
X = torch.rand(4, 2, 3, 5)
print(X.shape)

# padding(1, 2)  意思是行（上下）分别增加一行0，列（左右）分别增加一列0
# 卷积层结构参数输入通道数等于X通道数，Kernel size整体小于等于X的size
conv2d = nn.Conv2d(in_channels=2, out_channels=3, kernel_size=(3, 5), stride=1, padding=(1, 2))
Y = conv2d(X)
print('Y.shape: ', Y.shape)
print('weight.shape: ', conv2d.weight.shape)
print('bias.shape: ', conv2d.bias.shape)

5、池化层

分成均值池化与最大池化，以最大池化举例，二维互相关操作以感受野内最大值代替，同理均值以感受野内均值代替

池化层之后不做矩阵相加操作，也就是说输入数据经过池化后通道数不改变

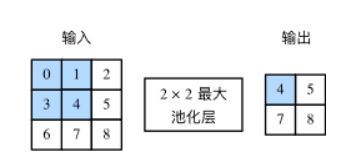
Pytorch实现

# 主要运用了nn.MaxPool2d函数
# 均值池化 nn.AvgPool2d
X = torch.arange(32, dtype=torch.float32).view(1, 2, 4, 4)  #（1，2，4，4）尺寸，值为1-32的四维矩阵
pool2d = nn.MaxPool2d(kernel_size=3, padding=1, stride=(2, 1))
Y = pool2d(X)
print(X)
print(Y)

笔记内容来自动手学深度学习Pytorch版