慢教育Scratch教案分享：神奇的斐波那契数列

固定链接： https://www.kidscoding8.com/52348.html

我们先来了解一下什么是斐波那契数列。

 

假定一个数列，后面的每一项都等于前两项之和，如果从第0项开始，它的值是0 ，第1项是1，那么，这个自然数数列会是这个样子：

0，1，1，2，3，5，8，13，21，34，55，89……

可以用一个公式来表示：F（n）=F(n-1)+F(n-2)（n≥2，n∈N*）

这些数字就被称为斐波那契数（Fibonacci sequence）。

 

据说，这个规律是意大利数学家列昂纳多·斐波那契（Leonardo Fibonacci）在研究兔子繁殖的时候发现的，所以，又称作“兔子数列”。

 

兔子繁殖的故事是这样的：如果一开始有一对兔子，它们每月生育一对兔子，小兔在出生后一个月又开始生育且繁殖情况与最初的那对兔子一样，那么一年后有多少对兔子？

答案是，每月兔子的总数可以用以下数列表示：1，1，2，3，5，8，13，21，34，55，89，144，233…

 

这一数列看起来相当简单，但却隐藏着一些有趣的东西。

 

今天的慢教育scratch教案分享，我们试着用scratch程序来实现斐波那契数列，然后用这个数列来绘制一些漂亮的图形。

 

任务说明

 

首先，提示下，今天这个案例，我们首先是学习结构化的编程思路。简单的说，就是自己构建一个实现某种功能的积木块（相当于其他编程语言的函数），将一个大任务，“分而治之”。

 

通常情况下，程序的整体功能并非全部编写在一段脚本中，而是把整体功能划分为多个部分，每个过程实现程序的部分功能，最后将各个过程合并在一起。合理使用“结构化的编程”思路，使程序看起来更加清晰易读懂，也更便于测试和调试，以及后期的修改和维护。

 

在scratch中，有两种方法可以实现结构化编程，一种是“广播”机制，今天不详细介绍。第二种方式就是“创建自己的积木块”（只有scratch2中有此功能）。

 

在scratch2的更多模块中，可自定于积木块，和系统自带的各种积木块一样，自定义积木块也可以卡合到脚本中。具体创建积木块的方式，以及给积木块添加参数的方法，这里不做详细讨论，大家可自己去实践，不懂的同学可参看系统的帮助文件。

 

今天我们主要讲讲怎么用自定义方式，构建一个求任意一项斐波那契数的积木块，然后，调用这个积木块来画图。

 

任务分析

 

用计算机程序构建斐波那契数列，有很多方法。（今天留给大家的思考题，你还能用哪些方式，实现斐波那契数列？试着用scratch来实现。）

 

学过编程的同学，看到F(n)=F(n-1)+F(n-2)这个公式，第一反应是用递归法。

 

 首先我们来说说什么是递归，简单的来说，就是一个积木块（函数）需要调用自己来完成某种功能，这种调用就叫做递归。

 

但我们需要清楚一点，递归在使用的时候，并不是一直调用自己，我们需要给他一个停下来的时机。就像打仗一样，要知道进攻的路线，但如果遇到突发状况也要能及时撤退。所以我们的递归也一样，你需要给他一条前进路径也要给他一条返回路径。所以在使用递归策略时，必须有一个明确的递归结束条件，称为递归出口。

 

递归会让代码看起来很简洁， 但递归有它致命的缺点，就是效率是很低。所以，我们如果用递归法计算斐波那契的第五十个数，会让计算变得缓慢。

 

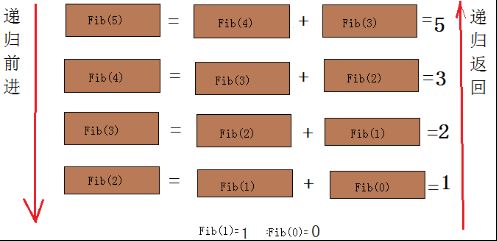
我们分析一下递归的执行过程，在斐波那契数列中，我们计算第五项的话，递归的过程是这样的：

 

 

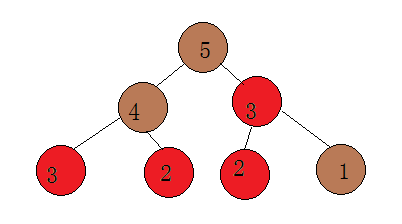
可能这样你还看不出问题，其实上面的图相当是一个树状结构：

     

 

红色的部分在之后又会被求到，如果我们给的数值不是5是一个更大的数，则被重复计算和调用的数和次数会变得更多。可见，在这样一个过程中，我们把某些值一直在重复计算，使得它的效率变得非常低，你们可以试着求一下第40 、50个斐波那契数。

 

现在我们换一种方法，来构建一个斐波那契数列积木块（函数）。

 

首先，我们定义四个变量：

 

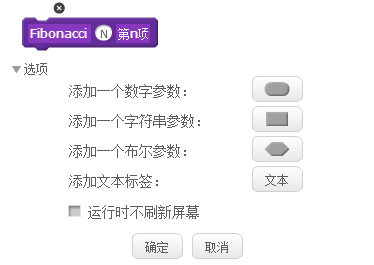
然后，在更多模块选项里面，点击新建功能块，输入一个便于识别和阅读的名称定义功能块的名称。

 

 

展开选项，可添加参数，前三项是不同类型的参数，我们这里选择数字参数，每个参数前，都可添加一个文本标签，作为参数说明。

 

 

 

参数添加完成后，在编程区，会出现这个起始积木块，然后我们根据规划的功能，添加不同的积木，来实现这个自定义积木块的功能。

 

 

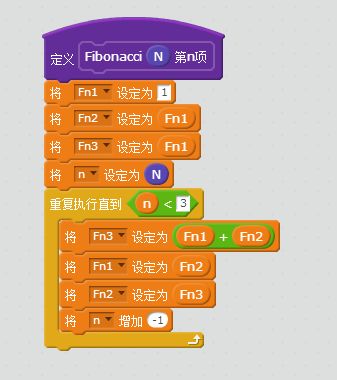
分析斐波那契数列的定义，我用迭代法来实现，代码如下：

 

 

首先，初始化四个自定义变量的值。定义第一项的值为1，再将第一项的值赋于第2、3项。设定变量n等于积木块传递的参数值，拥有控制循环次数。

 

然后，通过三个变量的迭代，用一个循环，可以很简洁的计算出第N项的值。（这里变量Fn3的值便是N项斐波那契数列的值。）

 

积木块构建完成。至此，我们可以调用这个积木块，计算出任意一项的数值。

 

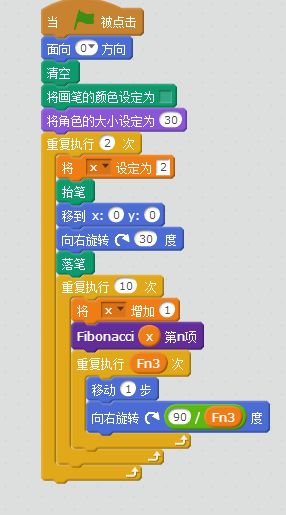
下面我们演示，怎么调用这个积木块，画一条斐波那契曲线。

 

 

这段代码运行的结果是这样的：

据说，达芬奇著名的蒙娜丽莎，就是符合斐波那契曲线构图的。

 

 

因为斐波那契数列中，后一项除以前一项数，随着数值的增大，结果会无限趋近与一个数：1.61803398875…

 

是不是很眼熟？

 

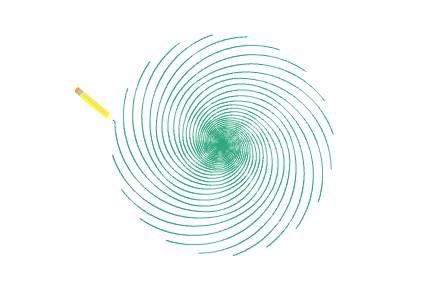
是的，这个数就是所谓的黄金分割。这也许说明了斐波那契数列与黄金分割有天然的联系。这条曲线也被称作为黄金螺旋。

 

我们来看看存在于自然界中的神奇黄金螺旋：

 

飓风云图

 

 

银河极也有相似的曲线

 

 我们转动一个角度，再画一条斐波那契曲线，看看是什么效果。

 

 像不像这货呢？

 

 

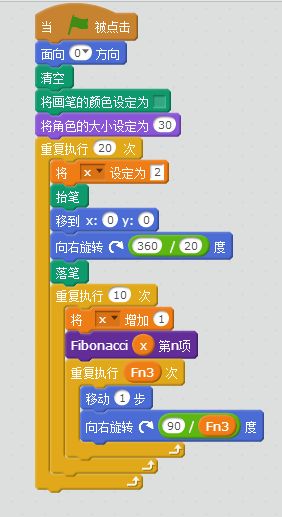
我们再继续画斐波那契曲线，将循环次数增加到20次。

 

结果是这样的：

对比下，向日葵里面是不是隐含着很多神秘的斐波那契螺旋？

 

 

据说，很多植物的特征都暗合斐波那契数的规律

 

 

仙人掌中也有斐波那契螺旋的影子

 

松果是最典型的例子

 

 
还有蓟、菊花、菠萝……都是按这种方式生长的

 

每层树枝的数目也往往构成斐波那契数列

 

据说，这样的布局能使植物的生长疏密得当、最充分地利用阳光和空气，所以很多植物都在亿万年的进化过程中演变成了如今的模样。

 

 

总而言之，斐波那契数量似乎暗合某种神秘的力量。不过，要说花瓣数也符合斐波那契数列，我觉得，也许仅仅是巧合？

 

毕竟，还有很多花的花瓣数不在斐波那契数列里面，譬如著名的十字花科族群。

 

 

 最后，让我们来膜拜下，发现这个规律的意大利人

 

 

-End-