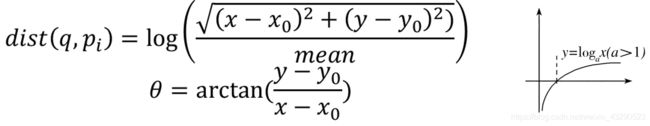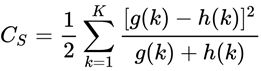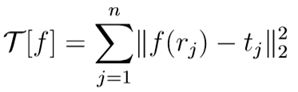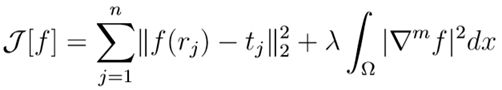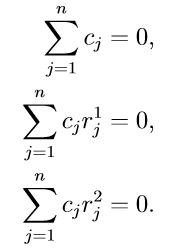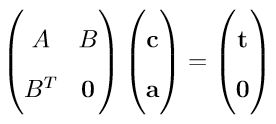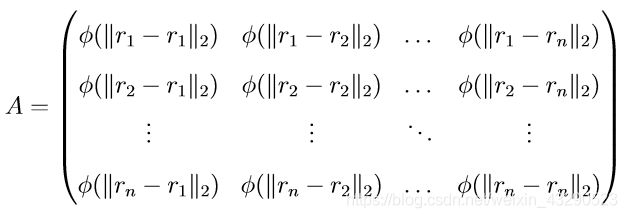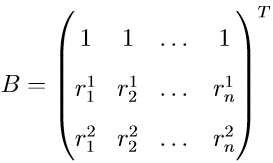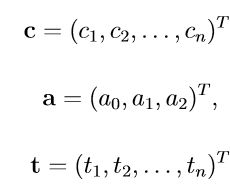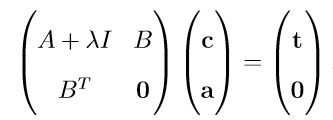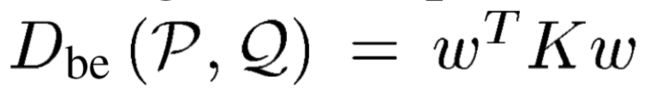形状上下文(shape context)算法完全解读

前言

一般来说，在计算机视觉任务中，形状匹配可以分为

1. 基于特征(Feature-based): 基于傅里叶变化、特征点的、骨架的等等。
2. 基于亮度 (brightness-based): 更偏向于使用像素的灰度值来进行形状匹配。

形状上下文作为一种基于特征的描述子，根据两幅图片轮廓采样点之间的相互关系(如距离、梯度)，提供了一种较为鲁棒的形状匹配策略。

下面我们一步一步来探讨形状上下文算法。

一. 轮廓提取(Canny Edge Detection)和轮廓点采样(Jitendra’s Sampling)

轮廓提取

对于轮廓的提取，我们采用canny算子，主要步骤分为

1. 高斯平滑
2. sobel提取梯度幅值和方向
3. 非极大抑制
4. 双阈值检测以及连接(滞后门限处理)

这里不再细说，下面带大家看一看轮廓采样这一步骤。

轮廓采样

对于一般图像，如果采样给定个数的像素点，我们可以使用均匀采样、随机采样、等间隔采样等方式。但是对于二维轮廓点集来说，因为它的分布并不是均匀的，所以这些方法并不适用。

图1、图2是使用canny算子提取的轮廓，图3、图4是随机采样100个点得到的采样结果，可以看到采样过后轮廓信息出现了一定的丢失。如果我们想得到图5、图6这样的采样结果，该如何去做呢？

一种朴素的想法就是：我们是否可以将轮廓点对之间的欧式距离考虑到采样步骤中，得到一个 相对均匀(或者说是，点对间足够分散) 的的轮廓采样结果呢？比如说，每次剔除最短距离点对中的任意一个点，并解除它与其他点之间的距离关系，依次重复，直至点对只剩下所需数目的点集。

这个就是Jitendra’s sampling的思路，下面附上Jitendra采样的流程：

一些Tips:

1. 第一步需要对轮廓点进行随机重排，这样子可以保证删除点对的随机性，避免删除时产生连锁反应(l_ab>l_bc>l_cd>l_de,如果每次删除最小点对右值，则删除步骤可能变成了e→d→c→b→a)。
2. 其中阈值(k = 3)主要是针对于轮廓点过多而预设的一个倍数关系。如果轮廓点(I)>3×采样点(N)，直接对轮廓点集随机采样，取前3N个就行。
3. 可以先对点对距离进行排序，然后逐一删除符合条件(点对中的每个点都没有被删除)的右值(左值均可，规则统一就行)。

下面附上论文样例中这部分的Matlab源码：

function [xi,yi,ti]=get_samples_1(x,y,t,nsamp);
% [xi,yi,ti]=get_samples_1(x,y,t,nsamp);
%
% uses Jitendra's sampling method

N=length(x);
k=3;
Nstart=min(k*nsamp,N);

ind0=randperm(N);
ind0=ind0(1:Nstart);

xi=x(ind0);
yi=y(ind0);
ti=t(ind0);
xi=xi(:);
yi=yi(:);
ti=ti(:);

d2=dist2([xi yi],[xi yi]);
d2=d2+diag(Inf*ones(Nstart,1));

s=1;
while s
   % find closest pair
   [a,b]=min(d2);
   [c,d]=min(a);
   I=b(d);
   J=d;
   % remove one of the points
   xi(J)=[];
   yi(J)=[];
   ti(J)=[];
   d2(:,J)=[];
   d2(J,:)=[];
   if size(d2,1)==nsamp
      s=0;
   end
end

二. 形状上下文(Shape Context)直方图矩阵的构建及其相似度度量方法

对于轮廓中的点对，哪些信息对于形状匹配起到贡献呢？

1. 距离，
2. 角度，
3. 等…

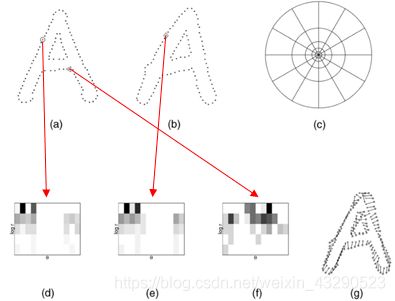
那么对于每个轮廓点，我们可以构建以其为中心的极对数坐标系 log-polar coordinates(包括12个角度区域和5个距离区域，如下图c)，再将它周围的轮廓点映射到每个区域内，然后统计落在每个区域的轮廓点数，最后进行归一化处理(即除以落在所有区域中的轮廓点数)。这样子我们就生成了形状上下文直方图矩阵。如下图所示，我们可以直观的看到，相似度_d-e > 相似度_d-f。

一些Tips:

1. 采用极对数坐标的好处：主要使得描述子对邻近采样点更敏感，强化局部特性。
2. 首先求出点对的距离矩阵，再除以距离均值，使形状上下文描述符对缩放不敏感。然后再将距离矩阵映射到对数域中，与阈值作比较。因为对数函数是单调变换，所以log域中的五个距离阈值可以映射到欧氏距离中(0.125,0.25,0.5,1.0,2.0, 这里大于2.0的点认为距离目标点太远，因此不考虑)后，再将距离矩阵与阈值比较，可以去除log运算的时间成本。如下图:

% use a log. scale for binning the distances
r_bin_edges=logspace(log10(r_inner),log10(r_outer),5);

3. 角度矩阵的求法也是如上图，相对简单。

4. 求解完距离矩阵和角度矩阵就可以做区域映射了，统计各个区域内点数。如果这里我们采样100个轮廓点，将会生成100×60大小的矩阵。

5. 别忘了做归一化处理。

此时，形状上下文直方图矩阵就构建完成了。下面我们使用卡方统计χ² 来计算点_输入图与点_模板图的相似度。

经过之前的计算，我们获得了输入图像 和模板图像 的N(100)×K(60)的形状上下文直方图矩阵，对于输入图像和模板图像中的每一个点，都有K维的直方图向量，分别记作 g(k) 和 h(k), 并代入卡方公式计算相似度度量矩阵:

此时我们就得到了关于形状上下文的相似度度量矩阵(N×N)。

这里解释一下为什么是N×N的矩阵：输入和模板图像均采样N个轮廓点(也可以采样不同的轮廓点数，再通过后续我们所说的伪点策略做匹配)，然后对于两张图片每个点对，将 g(k) 和 h(k) 带入卡方公式，可以计算出一个C_s。所以一共生成了N×N的矩阵。

三. 局部外观(Local Appearance)描述矩阵的构建及其相似度度量方法

根据形状上下文直方图矩阵，我们获得到了全局信息，即全局点对目标点的一个方位矩阵,类似于在不同方向、角度轮廓上点集的密度。那么接下来，我们考虑再添加一个局部外观信息来约束局部特征。

局部外观信息有很多，例如

1. 局部方向(local orientation)
2. 局部颜色直方图(local color histogram)
3. 局部纹理(local texture)
4. 局部拓扑(local topology)
5. 等等…

我们在这里考虑使用局部方向(local orientation) 作为形状上下文的局部外观信息。

1. 对于输入图像 和模板图像，我们计算相应灰度图的梯度Gx和Gy，然后找到轮廓点对应的梯度值并求出切向角 θ₁，θ₂。
2. 这里我们引入切向角非相似性(tangent angle dissimilarity)函数作为衡量局部方向的依据:

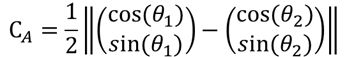
为什么可以这么定义呢，我们来看下图，假设有一个半径为1的圆，那么对于 θ₁，θ₂，通过余弦和正弦将其转化到欧氏空间中，再计算它们的欧式距离，就可以衡量两个角度的相似性了。

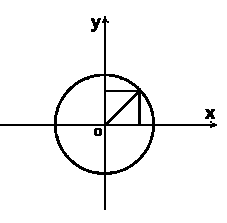
一些Tips:
可以对切向角非相似性函数做变换，得到一个简单的计算公式：

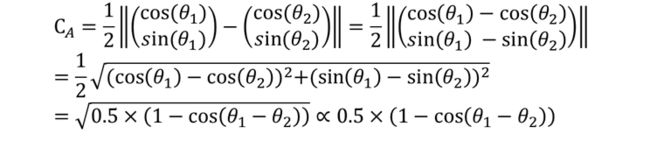
最后一步就是将两个相似度度量矩阵进行加权求和，输出总相似度度量矩阵:

C_s对应于形状上下文(Shape Context), C_A对应于局部外观(local Appearance),论文给的 β=0.1。

四. 匈牙利匹配(Hungarian)策略

匈牙利匹配是一种常见的二部图匹配，复杂度O(N³)，常用的场景有：

1. 寻找最大匹配问题，也就是寻找增广路径的过程：
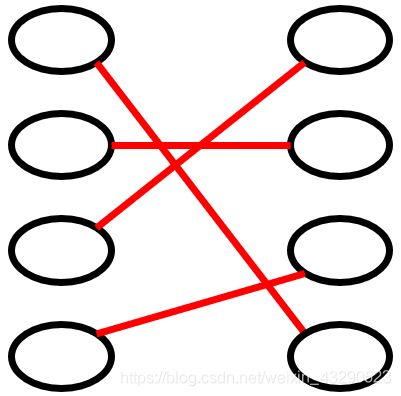
   给定匹配关系，找出使得匹配数最多的一种匹配。如下图,最大匹配为3，即L1-R2, L2-R3, L3-R1。我们不细说该方法的实现(深度或广度优先匈牙利)，大家如果有兴趣可以尝试尝试。
   
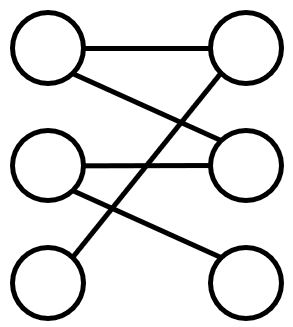
2. 寻找最短路径的问题：给定N对N个点对的距离，求出使得总距离最小的点对匹配关系。

在这里我们将之前的相似度度量矩阵抽象成距离矩阵，使用匈牙利算法的目的就是求出使得总损失最小的点对匹配。具体步骤如下：

1. 变换距离矩阵A_ij→B_ij，使得B_ij的各行各列都有0
2. 尝试分配，如果得到最优解，返回最小损失，否则进入(3)
3. 做最少直线覆盖所有0元素，转到(4)
4. 距离矩阵增加额外0元素，转到(2)

下面给出两个例子：

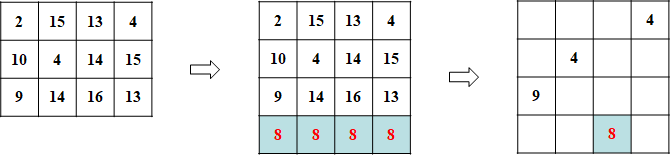
1. 如下图所示，给出4-4点对的距离矩阵。

• 每行减去相应行的最小值(图1→图2)，此时并非每行每列均有0元素。
• 每列减去相应列的最小值(图2→图3)，此时每行每列均有0元素。
• 判断是否得到最优解，我们发现此时形成完全匹配，流程结束。
• 最短距离 Dist_min = 4+4+9+11 = 28。

对应的匹配关系如下：

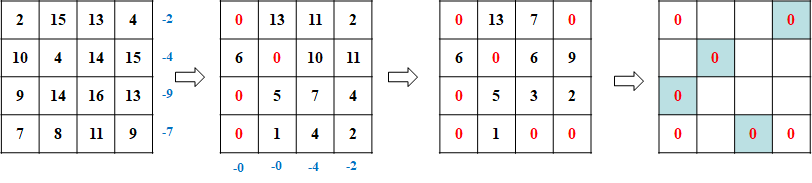
2. 如下图，给出另外4-4点对的距离矩阵。

• 每行减去相应行的最小值(图1→图2)，此时并非每行每列均有0元素。
• 每列减去相应列的最小值(图2→图3)，此时每行每列均有0元素。
• 判断是否得到最优解，我们发现此时并没有形成完全匹配。
• 做最少直线覆盖所有0元素，添加额外0元素，即所有没有被直线覆盖的元素减去最小值，直线相交的元素加上最小值(图4→图5)。
• 判断是否得到最优解，我们发现此时形成完全匹配，流程结束。
• 最短距离 Dist_min = 2+4+1+8 = 15。
• 最后，图7展示了对应的匹配关系。

我们想一想为什么可以这么做：

1. 因为距离矩阵的这种对应关系，无论我们按行(列)减去相应行(列)的最小值，都不会影响距离排序。
2. 参照例2，在添加额外0的那一步，我们将没被直线覆盖的矩阵取出，各个元素减去最小的元素e，当我们再把这个矩阵放回去的时候，为了维持距离排序关系，我们需要将14和44位置对应的0元素也减去e，或者将24和34位置加上e。

下面链接是匈牙利算法在线测试的链接：

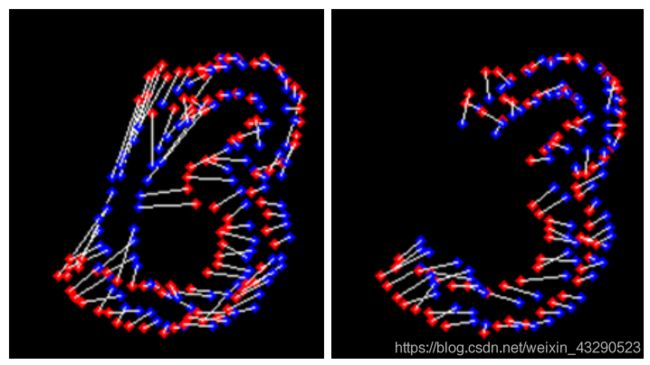
经过匈牙利算法后，两幅图片(digit-0,digit-3)的对应关系就找到了，我们将对应关系用白线连接起来：

由上图可以直观的发现，大部分的点对关系已经找到。但是仍然有一部分（中间）点对硬生生的进行了匹配。这是我们不太希望的。我们是不是可以添加一个阈值，使得这些匹配损失非常大的点对不进行匹配呢？

下面我们引入了伪点匹配。

五. 伪点匹配

通过添加伪点，

1. 解决两幅图像轮廓点数不同的情况。
2. 剔除一些匹配损失过大的点对匹配（离群值检测-outlier detection）

下面我们具体看一看如何实现伪点匹配。

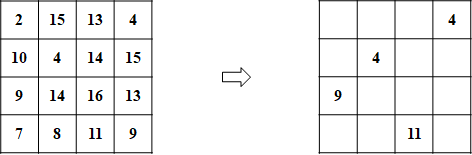
1. 如果距离矩阵不是N×M(M>N)，如下图1:

• 添加（M-N）行损失为thresh（=8）的矩阵进行补全，使其成为方阵。这M-N个点即为伪点（dummy point）。
• 再利用匈牙利算法做匹配。
• 删除与伪点相匹配的点。
• 最短距离 Dist_min = 4+4+9 = 17。

2. 离群点检测和剔除。下左图给出4-4点对的距离矩阵。如果不添加伪点，求得的最小距离如下右图。
   
   下面考虑添加伪点的情况。

• 添加R行R列损失为thresh（=8）的矩阵进行拓展，这2R个点即为伪点（dummy point）。
• 再利用匈牙利算法做匹配。
• 删除与伪点相匹配的点。

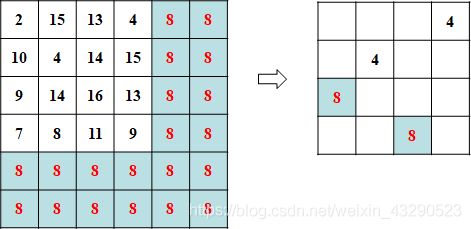
这意味着，对于点A，如果此时没有其损失小于阈值的匹配点可用时，将被分配一个伪点。

下图展示了伪点匹配对于匹配结果的影响，左为不添加伪点的情况，右为添加伪点的情况：其中伪点个数为轮廓点的0.25，且损失为0.25。

1. 添加伪点使得轮廓对于噪声鲁棒性增强，但是也意味着对于下一次的迭代（经TPS变形的图像，将在下一节介绍TPS），形状上下文矩阵以及相似度矩阵都会因离群点的出现而作相应的变化：即不在考虑离群点的贡献。
2. 同时我们仍然要获取这些离群点的形状上下文，因为可能经过下一次的变形，这些离群点又会成为内点(inlier points)。具体可以参考matlab源码。

六. 薄板样条插值（Thin Plate Spline）进行轮廓点拟合

通过匈牙利以及伪点匹配策略，我们从2N个轮廓点中获得了S个匹配度很高的匹配点对。我们又萌发了一种想法：就是能不能通过这S个匹配点对，将输入轮廓做一次变形，使其更加接近于模板轮廓呢？然后对于变形后的轮廓与模板轮廓，再次寻找匹配度高的匹配点对呢？

于是我们引入了薄板样条插值（TPS）函数来对输入轮廓做变形，使得总弯曲能量达到最小。

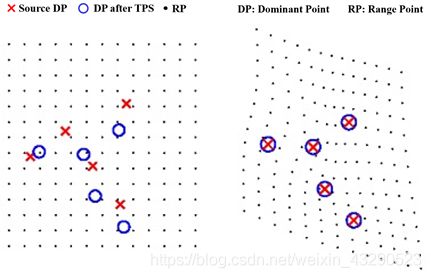
薄板样条插值是一种常见的插值方法，经常用于二维图像配准中。通过将N个主点（Dominant Point）变形到对应位置，求出相应的位移场，然后计算其他区域点变换后坐标。如下图：

对于一般插值方法而言，插值的首要约束就是：

给定插值点(r_j, t_j)，设法构造一个连续光滑的函数y = f(x),使得函数曲线（面）通过所有插值点，即f(r_j)=t_j。于是目标函数可以写成一下形式：

对于多谐波样条插值(Polyharmonic Spline)而言,添加基于梯度的平滑项（正则项）：

薄板样条插值是多谐波样条插值的特例（m=2）

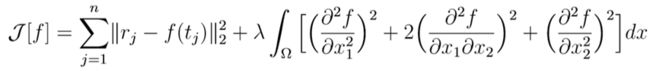
我们将正则化项中λ称为正则化参数，积分部分称为弯曲能量，即：

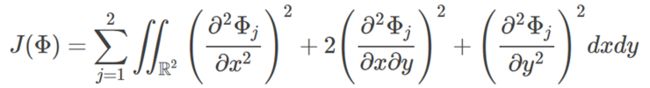
我们可以把薄板样条插值函数想象成一个弯曲的薄钢板，使它穿过顶点，找到使得弯曲能量最小的插值函数。

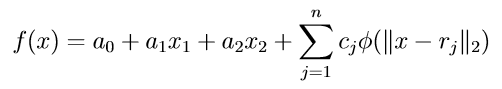
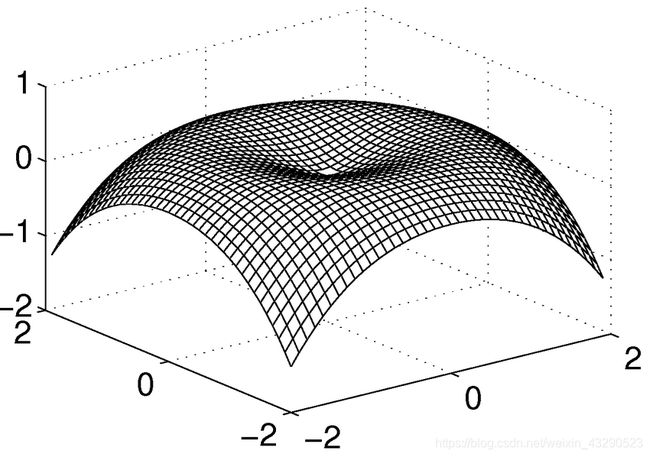
其中Φ( r ) = r²lnr 是TPS的径向基核函数，其二维图片如下：

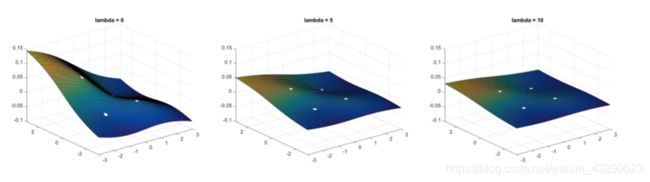
经[1]证明，f(x)上述函数是使得弯曲能量最小的插值函数。它可以看成非变形项/线性项（a₀+a₁x+a₂x）加上变形项（后面部分）构成。线性项定义了一个平面对于所有控制点的最佳匹配，可以看成最小二乘拟合，而非线性项可以看作与控制点提供的弯曲率有关。如下图，当正则化参数λ越大时，越接近于最小二乘拟合。

由于插值函数有N+3个条件，而我们有N个（点对）约束，于是我们再添加3个约束条件，如下：

这三个条件连同插值条件一起，可以写成如下矩阵形式：

再将正则化参数λ带入求解(在文末公式推导中),，可得

最终求得

1. 弯曲能量 D_be = mean(diag(w^T(A)w))
2. 形变损失（Affine Cost） = log(svd(s(1)/s(2))，其中s = svd(a)。
3. 轮廓点变换后坐标。

下面附上论文样例中TPS/Bookstein 的Matlab源码并给出注释：

function [cx,cy,E,L]=bookstein(X,Y,beta_k);
% [cx,cy,E,L]=bookstein(X,Y,beta_k);
%
% Bookstein PAMI89

N=size(X,1); 	% 轮廓点集1
Nb=size(Y,1); 	% 轮廓点集2

if N~=Nb 	% 判断轮廓点集是否相同
   error('number of landmarks must be equal')
end

% compute distances between left points
r2=dist2(X,X) 	% 求距离

K=r2.*log(r2+eye(N,N)); % add identity matrix to make K zero on the diagonal 求A矩阵（径向基部分）
P=[ones(N,1) X]; 	% 构造B矩阵
L=[K  P
   P' zeros(3,3)];	% 构造L矩阵 (Lc = V)
V=[Y' zeros(2,3)]; 	% 构造V矩阵
if nargin>2
   % regularization
   L(1:N,1:N)=L(1:N,1:N)+beta_k*eye(N,N); %如果有正则化项
end
invL=inv(L); 		% 求L的逆

c=invL*V';		% 求c矩阵 这里c = [c a]T
cx=c(:,1); 		% x方向
cy=c(:,2); 		% y方向

if nargout>2
   % compute bending energy (w/o regularization)
   Q=c(1:N,:)'*K*c(1:N,:);
   E=mean(diag(Q)); 	% 求解弯曲能量
end

在多轮迭代过程中求取经TPS变形后的图像与模板图像之间的形状上下文，再使用匈牙利匹配寻找点对关系。如下图（左为变形过程及各个损失的输出值，右为匈牙利算法求得的匹配点对）：

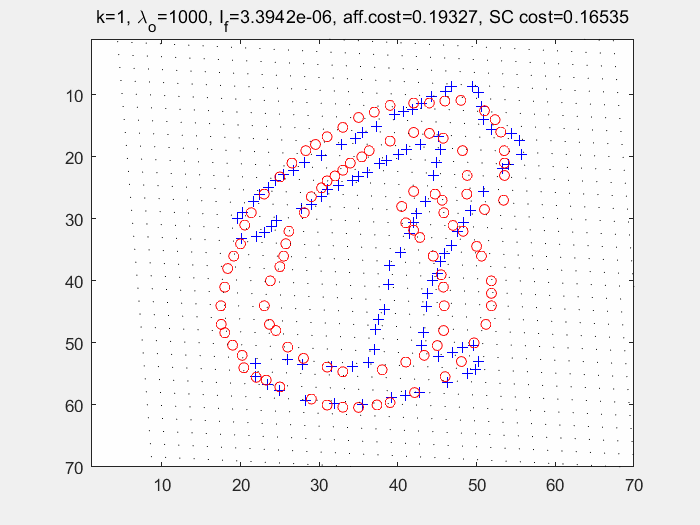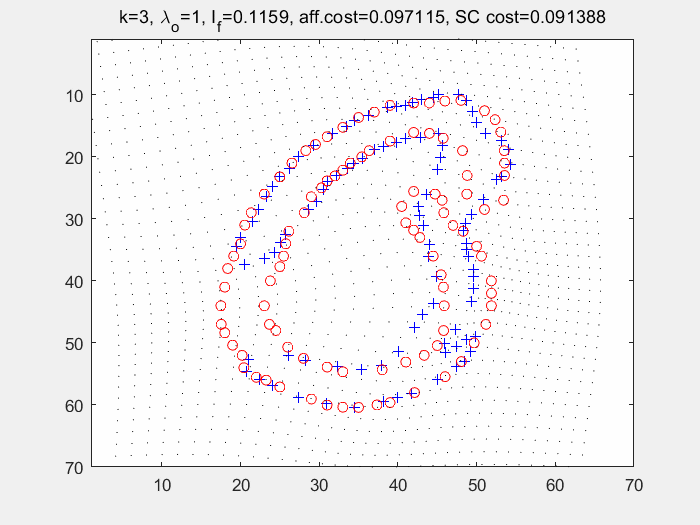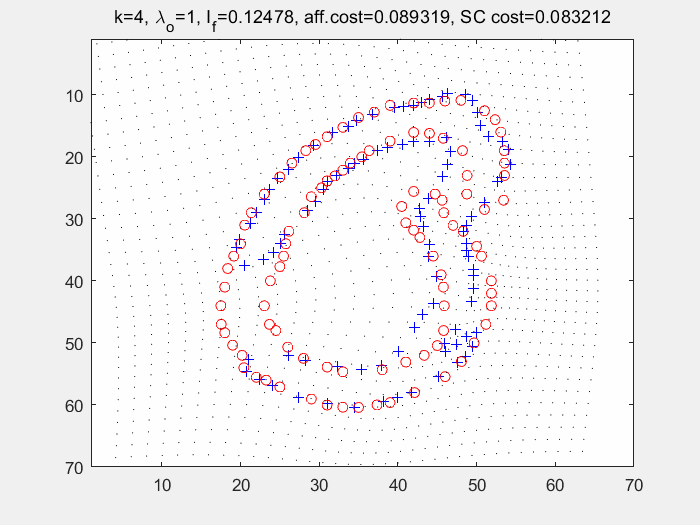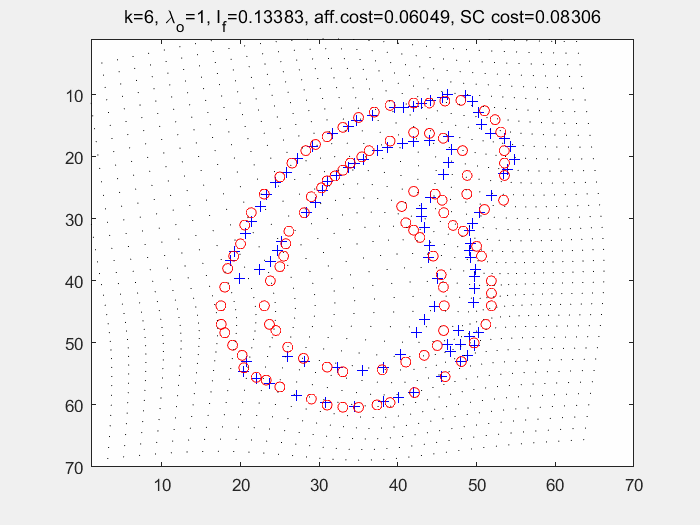
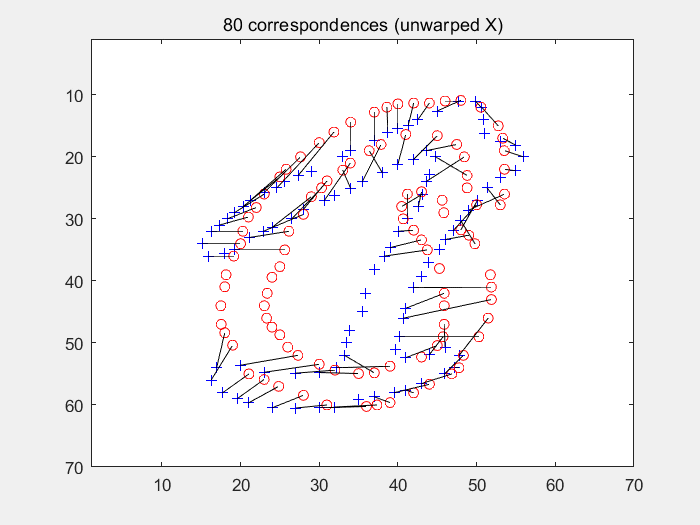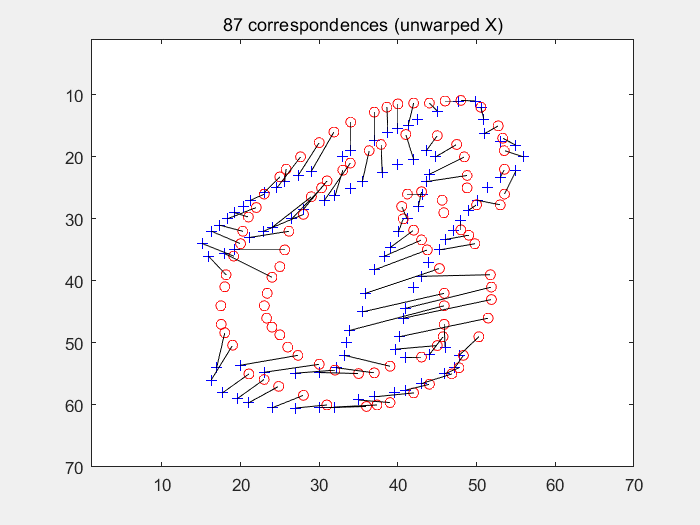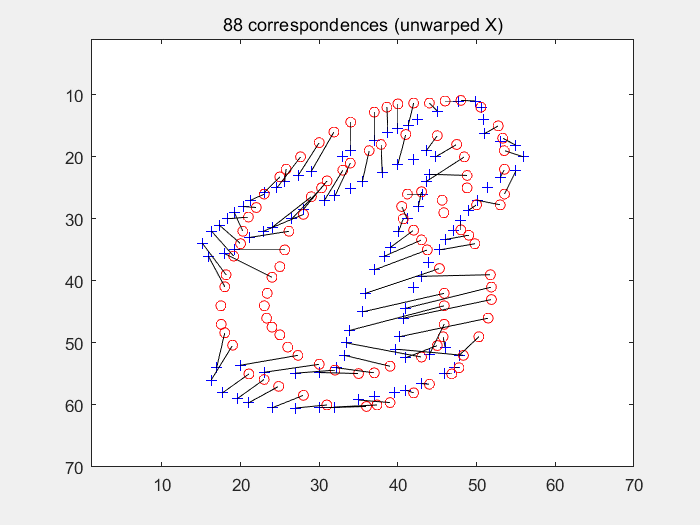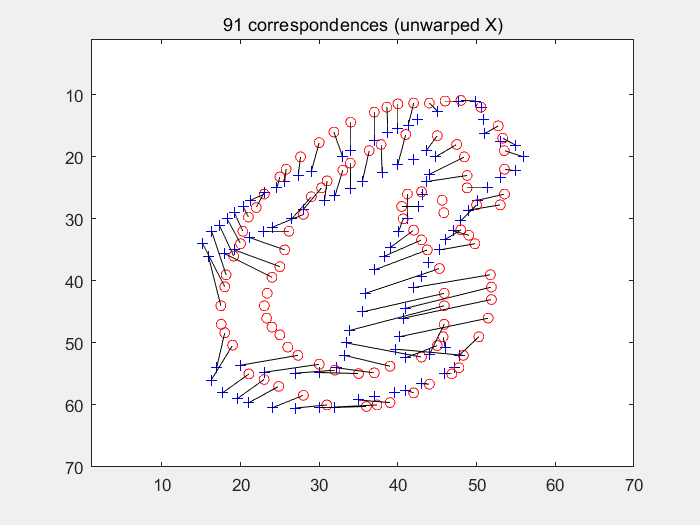
七. 损失函数计算和k-NN分类器进行分类

经过多轮(n = 5)迭代之后，我们就可以计算总损失来判断输入图像和模板图像的相似度了：

1. 形状上下文距离D_sc:
   形状上下文距离通过使用对称加和来得到，即对于总相似度度量矩阵，加权每行最小损失值除以列数以及每列最小损失值除以行数。公式如下：
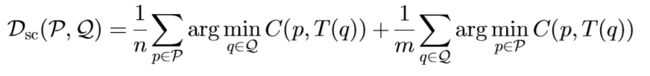   其中T为Q(输入图像)的TPS变换。

2. 外观距离D_ac:
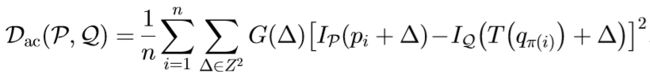   通过高斯窗函数，求出以P(模板图像)中轮廓点及经过TPS变换后的Q(输入图像)中轮廓点为中心及周边的亮度差平方的均值。

3. 弯曲能量距离D_be:
   
   弯曲能量为薄板样条插值函数求得的值。

最后使用经验公式来求出模板和输入图像的相似度，公式如下：

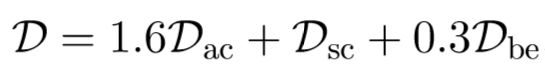
也可以用该相似度作为k-NN分类器的分类指标来进行数字识别。

八. 总结

最后给出形状上下文（Shape Context）的流程：

以及，形状上下文论文以及matlab实现的地址
如果想深入理解薄板样条插值及推导过程，附上薄板样条插值源论文(1篇)以及对应公式的推导(2篇)的下载链接

九. 一些改进

• 基于内距离的形状上下文 - IDSC (Inner Distance Shape Context)：针对于欧式距离在肢体变化中度量差的改进。
• 软判决形状上下文 - SSC (Soft Shape Context)：针对于直方图量化时边界误差的问题而提出的方法。
• 模糊形状上下文 - FSC (Fuzzy Shape Context)：根据隶属度函数获得模糊的直方图特性。
• 顺序形状上下文 - OSC(OrderedShape Contexts): 根据轮廓点顺序关系改进形状上下文。
• 等等…

[1] Kent, J. T. and Mardia, K. V. (1994a). The link between kriging and thin-plate splines. In: Probability, Statistics and Optimization: a Tribute to Peter Whittle (ed. F. P. Kelly), pp 325–339. John Wiley & Sons, Ltd, Chichester. page 282, 287, 311
[2] Belongie S , Mori G , Malik J . Matching with shape contexts[C]// IEEE Workshop on Content-based Access of Image & Video Libraries. IEEE Computer Society, 2000.
[3] Belongie S , Malik J , Puzicha J . Matching Shapes[C]// IEEE International Conference on Computer Vision. IEEE, 2001.
[4] Belongie, S, Malik, J, Puzicha, J. Shape matching and object recognition using shape contexts[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2002, 24(4):509-522.