单层感知机(Single Layer Perceptron)原理及Matlab实现
单层感知机(Single Layer Perceptron)原理及Matlab实现
- 前言
- 单层感知机
- 学习策略
- 损失函数的构造
- 损失函数的最优化求解
- matlab实现
- 动态可视化过程
前言
本文参考李航老师的《统计学习方法》,使用matlab实现简单的单层感知机(single layer perceptron)模型。
单层感知机
单层感知机作为一种简单的线性二分类模型,是神经网络(Neural Network)和支持向量机(SVM)的基础。
- 输入:实例的特征向量。输出:实例的类别。类型:判别模型。
- 目标:通过寻找一个
超平面(super hyper plane)将训练集中正负实例划分正确。 - 缺点:只能解决
线性可分的问题,且不能保证间隔最大的性质。
下图展示了单层感知机对于给定线性可分数据集(linearly separable dataset)的分割效果:
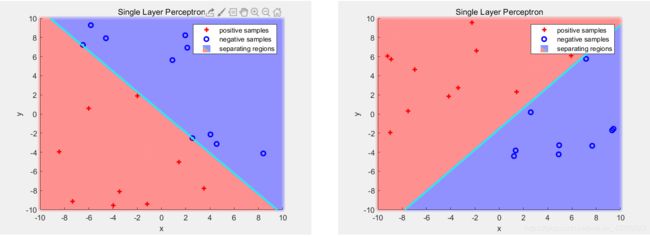
那么给定数据集:
D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x n , y n ) } D = \lbrace (x_1,y_1),(x_2,y_2),...,(x_n,y_n) \rbrace D={(x1,y1),(x2,y2),...,(xn,yn)}其中 x i ∈ R n x_i\in\bold R^n xi∈Rn为我们的数据, y i ∈ { + 1 , − 1 } y_i\in\lbrace+1,-1\rbrace yi∈{+1,−1}为对应数据的标签。
对于感知机模型就是要寻找一个超平面:
w ⋅ x + b = 0 w\cdot x + b = 0 w⋅x+b=0可以将正负实例完全分隔开,其中 w w w为权值向量, b b b为偏置(bias)。即
- 对于正样本有 w ⋅ x + b > 0 w\cdot x + b > 0 w⋅x+b>0
- 对于负样本有 w ⋅ x + b < 0 w\cdot x + b < 0 w⋅x+b<0
如下图所示(图源:统计学习方法):
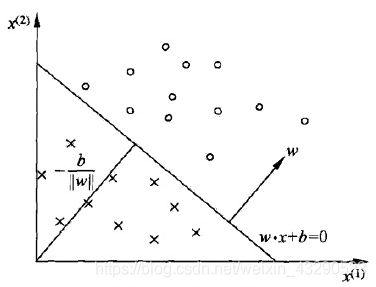
对于为什么正负样本带入超平面方程异号的问题,可以使用点到直线法向量的投影证明。如下:
d s i g n e d = w x 0 + b ∣ ∣ w ∣ ∣ d_{signed} = \frac{wx_0+b}{||w||} dsigned=∣∣w∣∣wx0+b
学习策略
我们希望找到一个损失函数来表示超平面对数据集的分割好坏。
损失函数的构造
首先我们应该找到一个评价指标/损失函数来评价我们模型的好坏。一种直观的想法就是统计误分类点的总个数 N e r r N_{err} Nerr,然后最小化损失:
arg min w , b N e r r \argmin_{w,b} {N_{err}} w,bargminNerr其中 w , b w,b w,b为感知机的模型参数。
但是这样定义的损失函数并不是关于参数 w , b w,b w,b的连续可导函数,不容易优化。
另一种想法就是统计误分类点 x i x_i xi到超平面的距离和,然后最小化该损失函数。点到直线距离公式为:
d = ∣ w x 0 + b ∣ ∣ ∣ w ∣ ∣ d = \frac{|wx_0+b|}{||w||} d=∣∣w∣∣∣wx0+b∣因为对于误分类点,存在: − y i ( w ⋅ x + b ) > 0 -y_i(w\cdot x+b) > 0 −yi(w⋅x+b)>0,所以可以通过引入 y i y_i yi去绝对值:
d = − 1 ∣ ∣ w ∣ ∣ y i ( w ⋅ x 0 + b ) d = -\frac{1}{||w||}y_i(w\cdot x_0+b) d=−∣∣w∣∣1yi(w⋅x0+b)于是我们定义损失函数:
L = − 1 ∣ ∣ w ∣ ∣ ∑ x i ∈ M y i ( w ⋅ x 0 + b ) L = -\frac{1}{||w||}\sum_{x_i\in M} y_i(w\cdot x_0+b) L=−∣∣w∣∣1xi∈M∑yi(w⋅x0+b)又因为感知机解决线性可分问题,损失函数最终收敛为0,所以权值项 1 ∣ ∣ w ∣ ∣ \frac{1}{||w||} ∣∣w∣∣1对收敛结果没有影响,反而会使学习过程复杂化。所以不考虑 1 ∣ ∣ w ∣ ∣ \frac{1}{||w||} ∣∣w∣∣1。
损失函数的最优化求解
这里使用随机梯度下降(SGD)来进行求解,不了解梯度下降的可以查看我之前的梯度下降(一)以及梯度下降(二).。
已知损失函数为:
L = − ∑ x i ∈ M y i ( w ⋅ x 0 + b ) L = -\sum_{x_i\in M} y_i(w\cdot x_0+b) L=−xi∈M∑yi(w⋅x0+b)求取梯度: ∇ w L ( w , b ) = − ∑ x i ∈ M y i x i \nabla_wL(w,b) = -\sum_{x_i\in M} y_ix_i ∇wL(w,b)=−xi∈M∑yixi ∇ b L ( w , b ) = − ∑ x i ∈ M y i \nabla_bL(w,b) = -\sum_{x_i\in M} y_i ∇bL(w,b)=−xi∈M∑yi
然后随机选取一个误分类点 ( x i , y i ) (x_i,y_i) (xi,yi),进行权值更新 w : = w + η y i x i w:=w+\eta y_ix_i w:=w+ηyixi b : = b + η y i b:=b+\eta y_i b:=b+ηyi其中, η \eta η为学习率。
经过多次迭代,损失函数收敛到0,超平面选取完成。
matlab实现
下面是单层感知机的matlab实现代码:
% Writen by Weichen Gu 4/24th/2020
clc; clf; clear;
Range = [-10, 10; -10, 10]; % set the range of dataset
dataSize = 20; % and the size of data
w = [-1;1];
b = 0; % Actual data parameters
[data, class] = generateLinearlySeparableDataSet(w, b, Range, dataSize); % Generate dataset
% Plot positive and negative data. pos: r+, neg : bo
figure(1);
hold on;
set(gca, 'XLim', Range(1,:));
set(gca, 'YLim', Range(2,:));
posFlag = find(class == 1);
negFlag = find(class == -1);
plot(data(1,posFlag), data(2,posFlag), 'r+','linewidth',2);
plot(data(1,negFlag), data(2,negFlag), 'bo','linewidth',2);
title('Single Layer Perceptron');
legend('positive samples','negative samples');
xlabel('x'), ylabel('y');
%Initialize w and b randomly;
w = randi([-100, 100], 2, 1);
b = randi([-100, 100]);
eta = 0.2; % Learning rate
lineX = linspace(Range(1),Range(3),100);
while(1)
funcMargin = class.*(w'*data+b);
errSampleIdx = find(funcMargin<=0);
% Using Stochastic Gradient Descent
errNum = length(errSampleIdx);
if(errNum == 0)
break;
end
idx = randi([1, errNum]);
[dx, db] = calculateGradient(data(:,errSampleIdx(idx)),class(errSampleIdx(idx)));
w = w - eta.*dx;
b = b - eta.*db;
end
lineMy = [lineX;-w(1)/w(2)*lineX-b/w(2)]; % Separating hyyperplane
h_line = plot(lineMy(1,:),lineMy(2,:),'c','linewidth',2); % draw separating hyyperplane
legend('positive samples','negative samples','separating hyperplane')
hold off;
%% generateLinearlySeparableDataSet
% Params Description:
% w - slope
% b - intercept
% Range = [RangeXL, RangeXR
% RangeYL, RangeYR]
function [data, class] = generateLinearlySeparableDataSet(w, b, Range, dataSize)
diff = Range(:,2)-Range(:,1);
data = (diff).*rand(2,dataSize)+Range(:,1);
val = w' * data + b; % seperating hyperplane w * x + b = 0; val > 0 positive samples val < 0, negative samples
% remove data on the seperating hyperplane
data = data(:,val~=0);
val = val(val~=0);
class = (val>0)-(val<0); % class(pos) = 1, class(neg) = -1
end
function [dw, db] = calculateGradient(x,class)
dw = -class.*x;
db = -class;
end
以及效果展示:
动态可视化过程
下面展示了单层感知机的动态可视化过程:
以及附上相关代码的下载链接,没有积分的朋友可以私信我发给你们
参考文献:
李航 -《统计学习方法(第二版)》