网易算法实习笔试复盘（选择题）

2020年4月7日19:00～21:00进行了网易算法实习生的笔试，答得一塌糊涂，因此对每道题进行复盘，希望能对未来的笔试有帮助，如果能帮到其他小伙伴就更好了。

1. B-树是一种多路平衡搜索树，如下图经常被简称为什么B-树？

答案：（2，3）-树

解释：B树，即B-树。其特点为如下：
①1 个结点可以存储超过 2 个元素；
②可以拥有超过 2 个子结点；
③拥有二叉搜索树的一些性质平衡；
④每个结点的所有子树高度一致，都比较矮。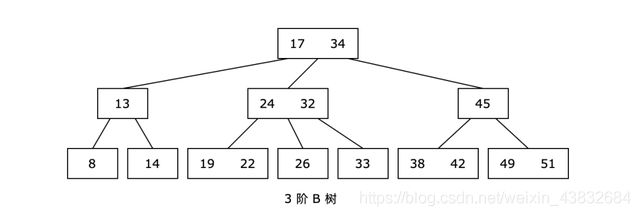

m 阶 B 树的性质（m ≥ 2）：
m 阶 B 树指的是一个结点最多拥有 m 个子结点。假设一个结点存储的元素个数为 x，那么如果这个结点是：
根结点：$1⩽x⩽m-1$
非根结点：$\lceil \frac{m}{2}\rceil -1⩽x⩽m-1$
如果这个结点有子结点，则子结点个数为 y = x + 1，那么如果这个结点是：
根结点：$2⩽y⩽m$
非根结点：$\lceil \frac{m}{2}\rceil ⩽y⩽m$

其中，向上取整（Ceiling），指的是取比自己大的最小整数，用数学符号$\lceil$ $\rceil$表示；向下取整（Floor），指的是取比自己小的最大整数，用数学符号 $\lfloor$ $\rfloor$表示。

• 比如 m=3，子结点个数 2≤y≤3，这个 B 树可以称为（2，3）树、2-3 树。
• 比如 m=4，子结点个数 2≤y≤4，这个 B 树可以称为（2，4）树、2-3-4 树。
• 比如 m=5，子结点个数 3≤y≤4，这个 B 树可以称为（3，5）树、3-4-5 树。以此类推。¹

2. 如果用 1×3 的瓷砖密铺 3×N 的地板（即不留下空隙），设 3×N 的区城铺瓷砖铺设方式为 dp[N] 种，试分析 dp[N] 的递推公式（N>3)?

答案：dp[N] = dp[N-1]+dp[N-3]

解释：假设3×n的区域铺瓷砖为f(n)，如果第一块瓷砖竖着，那么需要的方法是f(n-1)，如果横着铺，就是f(n-3)。
所以f(n) = f(n-1) + f(n-3)。
需要确定f(0)，f(1)和f(2)的值，容易知道，f(0)=f(1)=f(2)=1。接下来可以令n=需要的数字。²

3. 设计一个机器学习算法，通过 CT 影像鉴别病人是否患新冠肺炎，假设相比假阳性我们更重视假阴性，不希望漏掉病人，更准确的诊断可进一步通过核酸检验来完成。CT
   影像鉴别算法的准确率为 P，召回率为 R，则下列哪个指标作为该算法的性能指标较好？

答案：
$$F_{\beta }=\frac{(1+{\beta }^2)\cdot P\cdot R}{{\beta }^2\cdot P+R},其中\beta >1$$

解释：
表示分类正确：
TP（True Positive）：本来是正样例，分类成正样例。
TN（True Negative）：本来是负样例，分类成负样例。
表示分类错误：
FP（False Positive） ：本来是负样例，分类成正样例，通常叫误报。
FN（False Negative）：本来是正样例，分类成负样例，通常叫漏报。³

• 准确率（Precision）：准确率是针对我们预测结果而言的，它表示的是预测为正的样本中有多少是真正的正样本。
  $$P=\frac{TP}{TP+FP}$$
• 召回率（Recall）：召回率是针对我们原来的样本而言的，它表示的是样本中的正例有多少被预测正确了。
  $$R=\frac{TP}{TP+FN}$$

P和R指标有时候会出现的矛盾的情况，这样就需要综合考虑它们，最常见的方法就是F₁分数（F1-score）和F_β分数（F-score），通过计算F值来建立一个新的评价指标！⁴
F_β分数是一种衡量机器学习模型性能的指标，一般定义为⁵：
$$F_{\beta }=\frac{(1+{\beta }^2)\cdot P\cdot R}{{\beta }^2\cdot P+R}$$当β=1时，称为F₁分数(F1-score)，这时，准确率和召回率都很重要，权重相同。
当有些情况下，我们认为准确率更重要些，那就调整β的值小于1，如果我们认为召回率更重要些，那就调整β的值大于1。⁶

4. 某特殊队列允许在其两端进行入队操作，但仅允许在一端进行出队操作，入队的时候不许又出队操作，若元素1、2、3、4、5依次入此队列后再进行出队操作，则不可能得到的出队序列是？

答案：4，2，3，1，5

解释：初始时队列为空，元素1左入（或右入），而元素2无论是左入还是右入都必与1相邻，而这个选项中的1与2不相邻，不合题意。⁷

5. Bagging是常见的集成学习方法，它主要是从哪个角度增加了个体学习器的多样性？

答案：输入样本扰动

解释：
集成学习

• 主要思想：通过将多个学习器进行结合，获得比单一学习器更好的泛化能力。

• 对个体学习器的要求：“好而不同”
  （1）个体学习器要有一定的准确性：单个学习器的准确度越高，集成学习器才可能越好。个体学习器不能太差，至少不能差于弱学习器。（弱学习器是指泛化性能略优于随机猜想的学习器）
  （2）个体学习器的多样性（差异性）：学习器之间要有差异。

• 常见算法：
  ①Boosting
  ②Bagging
  ③Rondom Forest
  boosting各个学习器之间存在强依赖关系，各个学习器是串行方式生成的。bagging和random forest的各个学习器之间不存在强依赖关系，可以单独去训练（并行生成）。

• 结合方法：
  ①平均法：对数值型输出，可以采用平均法。
  -简单平均法;
  -加权平均法两种。

  ②投票法：对于分类任务常常可以采用投票法
  -绝对多数投票法：只有当某标记票数过半才预测为该标记，否则拒绝预测；
  -相对多数投票法：将票数最多的标记作为预测值；
  -加权投票法：对不同学习器采取加权方法投票；

  ③学习法：通过一个学习器来训练，使各个学习器结合起来。例如stacking算法（以初学习器的输出作为输入，训练学习器）。

• 增加个体学习器多样性：
  简单地利用初始数据训练出的个体学习器多样性一般比较差，我们可以在学习过程中利用对输入样本、输入属性、输出表示、算法参数进入扰动引入随机性来增强个体学习器的多样性。

  • 数据样本扰动（输入样本扰动）
    数据样本扰动对“不稳定基学习器”很有效，这样的“不稳定基学习器”主要有决策树、神经网络。训练样本稍微有些变化就会导致学习器有显著的变动。而有些基学习器对数据样本的扰动是不敏感的，比如线性学习器、支持向量机、朴素贝叶斯、K近邻学习器，这样的基学习器称为稳定基学习器，稳定基学习器对数据样本的扰动不敏感，对这类稳定基学习器一般采用的是输入属性扰动等其他机制。数据样本扰动基于的是采样法，在Bagging中使用的是自助采样法，而在AdaBoost中采样的是序列采样。
  • 输入属性扰动
    著名的随机子空间算法依赖的就是输入属性扰动，这个算法从初始属性集中抽取出若干个属性子集，再基于每个属性子集在子空间中训练个体学习器不仅能够产生多样性大的个体，还会因属性数的减少而大幅节省时间开销。
  • 输出表示扰动
    基本思路是对输出表示进行操纵以增强多样性。可对训练样本的类标记稍作变动，如“翻转法”，翻转法由Breiman在2000年随机改变一些训练样本的标记；或者是对输出表示进行转化，如“输出调制法”将分类输出转化为回归输出后构建个体学习器。还可以将原任务拆解为多个可同时求解的子任务。
  • 算法参数扰动
    这里的算法参数一般要对参数进行设置，比如神经网络的隐层神经元数、初始连接权值等，通过随机设置不同的参数，往往可产生差别较大的个体学习器。比如可以将决策树使用的属性选择机制替换为其他的属性选择机制。“负相关法”显示地通过正则化项来强制个体神经网络使用不同的参数。⁸

其中，Bagging方法是一种在原始数据集上通过有放回抽样训练分类器的方法。

算法步骤
假设训练集包含m个样本

1. 从m个样本中随机选取一个样本放入采用集中，再把该样本放回到初始数据集中，再次采用。重复m次采用，得到一个包含m个样本的采样集。
2. 重复步骤一T次，得到T个含m个样本的采样集，最终训练得到T个模型H₁，H₂，……，H_T。
   3.将这T个学习器结合，得到集成学习器。

结合方法：Bagging通常对分类任务，采用简单投票法。对回归任务，采用简单平均法。

注 : Bagging的这种自助采用方法，每个采用数据集大概用到了63.2%的样本，有36.8%的样本没有被采集到。这一部分数据可以用做验证集。⁹

6. 在支持向量机算法中，下列哪项不是超参数？

答案：支持向量的最少个数

解释：支持向量机的超参数包括：
（1）C: 目标函数的惩罚系数C，用来平衡分类间隔margin和错分样本；
（2）kernel：核函数；
（3）degree：决定了多项式的最高次幂；
（4）coef0：核函数中的独立项；
（5）gamma：正则化系数；
其中（1）和（2）为核函数，（3）和（4）为核函数的参数，（5）为正则化系数，而支持向量的个数不是超参数，而是算法的输出。

7. 在训练数据不足时，往往会产生过拟合现象，正则化是缓解过拟合的常用方式，下列关于 L1 正则化和 L2 正则化描述错误的是？

答案：L1正则的先验分布服从高斯分布，L2正则的先验分布服从拉普拉斯分布。

解释：

1. L1正则化：在原优化目标函数中增加约束条件${\Vert w\Vert }_1\le C$（L1范数作为惩罚项）；
   L2正则化：在原优化目标函数中增加约束条件$\Vert w\Vert {}_2^2\le C$（L2范数作为惩罚项）；
2. L1正则化可通过假设权重w的先验分布为拉普拉斯分布，由最大后验概率估计导出；
   L2正则化可通过假设权重w的先验分布为高斯分布，由最大后验概率估计导出；¹⁰
3. L1归纳偏好：学习到的模型权重稀疏；
   L2归纳偏好：学习到的模型权重平滑（方差较小）；¹¹

8. KNN方法和聚类方法通常都需要度量两个样本的距离（相似性），常见的几种度量方式有汉明距离，欧式距离，余弦距离等。假设已知两个样本的向量表示为[1,0,1]和[1,1,0]。那么欧式距离为________

答案：$\sqrt{2}$

解释：欧式距离，即欧几里得度量是生活中常中的计算距离的方式。在n维空间中，两点的距离为¹²：
$$d(x,y)=\sqrt{(x_1-y_1{)}^2+(x_2-y_2{)}^2+\cdots +(x_n-y_n{)}^2}=\sqrt{\sum _{i=1}^n(x_i-y_i{)}^2}$$

9. 一颗二叉查找树（BST）的节点数为 N，树的高度为H，N远大于H，那么随机删除一个节点，然后重新调整为一颗二叉查找树（即操作为：找到该节点的中序遍历的直接后继，交换节点的值，再删掉），那么平时时间复杂度最接近？

答案：O(N)

解释：
二叉查找树先序遍历、中序遍历、后序遍历时间复杂度均为O(N)¹³；
二叉查找树查找节点时间复杂度O(logN)；
直接后继时间复杂度为O(1)，其中直接前驱为节点的前一个节点，直接后继为己节点的后一个节点¹⁴；
二叉查找树删除节点时间复杂度O(logN)；
二叉查找树交换节点时间复杂度O(1)；
其中最复杂的事就是中序遍历O(N)。

10. 设随机变量X与Y相互独立，且X服从伯努利分布，Y服从正态分布：$X～B(1,\frac{1}{2}),Y～N(0,1)$，则概率$P\{XY⩽0\}=?$

答案：$\frac{3}{4}$

解释：$XY⩽0$在：
①$X⩽0$且$Y⩾0$；
②$X⩾0$且$Y⩽0$；
时成立。

X服从伯努利分布，也称为二项分布，X的取值只能为1或0。本题中，X取值为1的概率为$\frac{1}{2}$，取值为0的概率为$\frac{1}{2}$。
Y服从正态分布，本题中Y的期望为0，方差为1。

则：
①$X⩽0$的概率为$\frac{1}{2}$，$Y⩾0$的概率为$\frac{1}{2}$，联合概率为$\frac{1}{4}$
②$X⩾0$的概率为1， $Y⩽0$的概率为$\frac{1}{2}$，联合概率为$\frac{1}{2}$

所以：
$P\{XY⩽0\}=\frac{1}{4}+\frac{1}{2}=\frac{3}{4}$

---

1. 面试被问“红黑树”，我一脸懵逼…… ↩︎

2. 用1×3的瓷砖密铺3×20的地板有几种方式？ ↩︎

3. 准确率P 召回率R ↩︎

4. 谈谈准确率（P值）、召回率（R值）及F值 ↩︎

5. 机器学习笔记~F-score beta衡量precision和recall之间重要性 ↩︎

6. 分类模型的评估方法-F分数(F-Score) ↩︎

7. 拿offer-数据结构试题 ↩︎

8. 集成学习—如何增强个体学习器的多样性 ↩︎

9. 集成学习与常见算法-bagging、random forest、Boosting等 ↩︎

10. 理解：L1正则先验分布是Laplace分布，L2正则先验分布是Gaussian分布——复习篇 ↩︎

11. 【机器学习】深剖L1与L2权重正则化 ↩︎

12. 欧几里得度量_百度百科 ↩︎

13. 二叉树的前序遍历、中序遍历、后序遍历、层序遍历的时间复杂度和空间复杂度 ↩︎

14. 什么事线性表的直接前驱与直接后继_百度知道 ↩︎