智算之道复赛补题

菜得雅痞，签了个到就溜了，所以今天特来补题，看看能难成什么哼哼哼

第二题 网格

比赛的时候知道是dp，恨得牙痒痒，就是做不出，再加上那个数字大得令人发指，感觉根本存不下，就没有继续怼着做，玻璃心太容易被劝退了，这样可不行噢~⛽
换一种思维，我们不需要用一个棋盘那么大的二维数组去存到底是不是魔法点，我们直接用结构体数组记录下魔法点的下标不就好了？你看k的范围只在[0,2000]呢，不要害怕，你存不下不是计算机的问题而是你思维方式的问题，换一种思路让它能存下不就好了？
而且我们只需要初始化为根本不理会魔法点，然后用dp滚一遍魔法点取到最小就行了，记得用n封口，不然就到不了终点辣~还有就是把魔法点从小到大排序（排序要注意a.x!=b.x就改成a.x 这题暴露的大问题有两个：
①不能熟练运用数据结构去存下我要的数据，容易被大数字吓到，就不敢动手了；
②dp不熟，按理说这是很简单的贪心，但是就是打死也做不出说明不够烂熟于心。

#pragma GCC optimize(2)

#include
#include
#include 
#include
#include 
#include
#include 

using namespace std;

typedef long long ll;

const int maxn = 2005;//边长只到2000
ll f[maxn];
int n,k,w1,w2;

struct node
{
	int x,y;
}a[maxn];

bool cmp(node a , node b){//升序
	if(a.x != b.x) return a.x < b.x;//不等于才要排撒
	return a.y < b.y;
}

void solve(){
	scanf("%d%d%d%d", &n,&k,&w1,&w2);
	for (int i = 1; i <= k; ++i)
		scanf("%d%d", &a[i].x, &a[i].y);
	sort(a + 1, a + 1 + k, cmp);//从a+1开始啊
	a[1+k].x = n, a[1+k].y = n;
	k++;//封口
	for (int i = 1; i <= k; ++i)
		f[i] = 1ll * (a[i].x + a[i].y) * w1;//不走魔法路径
	for (int i = 2; i <= k; ++i)
	{
		for (int j = 1; j < i; ++j)
		{
			if(a[j].x < a[i].x && a[j].y < a[i].y){//严格小于
				 int num = a[i].x - a[j].x + a[i].y - a[j].y - 2;//从一个魔法点到另一个魔法点直走的路程
				 f[i] = min(f[i], f[j] + 1ll * num * w1 + w2);
			}
		}
	}
	printf("%lld\n", f[k]);
}

int main(int argc, char const *argv[])
{
	solve();
	return 0;
}

第三题 有向无环图

研究了一下午，我也发现了聚聚发现的规律！只不过我一直想着怎么从>=路径数的那个2的幂去减掉路径，而没有想到从<=路径数的那个2的幂去增加路径是我思维太局限了，而且聚聚求点数的方法也比我简单，唉太菜了。

#pragma GCC optimize(3)
#include 
using namespace std;

typedef unsigned long long ll;
int cnt = 2;
ll n,m,p;
struct No{
    int x,y;
};
vector<No>res;

int main()
{
    ll K,N;scanf("%llu%llu",&K,&N);
    ll temp = 1;
    while(temp<K){
        temp<<=1;
        cnt++;//点数
    }//temp是>=K的2的幂

    for(int i=1;i<cnt;i++)
        for(int k=i+1;k<cnt;k++)
            res.push_back(No{i,k});//先把1到(cnt-1)好点全部连好
        
    ll tempx = temp - K;
    for(int i=1;i<cnt;i++){
        if(i == 1) res.push_back(No{i,cnt});//至少还有1到cnt这条边
        else if((tempx>>(i-2)&1)==0) res.push_back(No{i,cnt});//这波位运算太美妙了！
        //要是转化成二进制之后最低位是0，就连2和cnt，要是倒数第二位是0，就连3和cnt
    }
    printf("%d %d\n",cnt,res.size());
    int sz = res.size();
    for(int i=0;i<sz;i++){
        printf("%d %d\n",res[i].x,res[i].y);
    }
    return 0;
}

说到这个有向无环图我想到了昨天夜场的C题就是一道无向有环图，

题目大意：
给你一个n，形成一个数列包括1~n共n个数，然后对于这n个数的每一个下标i，如果能找到最大的下标j（jPi那么i和j之间可以连一条无向边；或者如果能找到最小的下标j（j>i）并且Pj>Pi那么i和j之间可以连一条无向边，问其中可以形成环的数列有多少个？（取模）
分析：
我们可以发现无论左右都是要找一个数大于当前该数，左边找的话要下标尽量大，右边找的话要下标尽量小。分析可得，最大的一个数的位置很重要，因为最大的数在左右两边都找不到与之成环的元素，那么用这个最大数阻断最后一个数与前面数的连接即可。也就是让最后一个数只能找最大数连接，然后最大数又无法与其他数连接，就隔离开了最后一个数从而断掉了这个环。怎么让最后一个数只能找最大数连接呢？把最大数放在最后一个数前面一个也就是倒数第二个即可（因为往左找需要下标尽量大，而最后一个数只能往左找）

举个栗子：
[2,3,4,1]
我们可以形成(1,2) (2,3) (最大的元素4这里啥也形不成) (3,4)
于是(1,2) (2,3)可以成环，但漏掉了4，所以断掉了环。
怎么算呢？n个数排列共有n!种方法，我们要断掉环可以把数组想象成双向队列，元素1、2…(n-1)可以从首或者尾入队，但是最大元素n位置固定，只能在倒数第二个，所以有2^(n-1)种方法，所以，

你以为到这里就结束了吗？不，取模的时候还要小心，因为指数比阶乘的收敛速度快，所以不能直接ans%mod得结果，而是要(ans%mod+mod)%mod才可以避免出现负数，因为反正mod%mod=0嘛，所以+mod不影响结果，但是避免了负数的出现。

#include
using namespace std;
 
const int mod=1e9+7;
int n;
long long ans=1,x=1;
 
int main(){
	cin>>n;
	for(int i=1;i<=n;i++) ans=ans*i%mod;
	for(int i=1;i<n;i++) x=x*2%mod;
	cout<<((ans-x)%mod+mod)%mod<<endl;
	return 0;
} 

第四题 分数

这个题盲猜无脑打表TLE，介绍一个前置知识——欧拉筛。

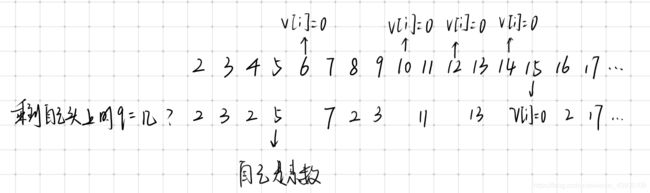
欧拉筛法的基本思想 ：在埃氏筛法的基础上，让每个合数只被它的最小质因子筛选一次，以达到不重复的目的。

模板如下：

void getprime() {
    for(int i = 2;i < maxn;i++) {
        if(v[i] == 0) {//是质数
            v[i] = i;a[++cnt] = i;//a数组记录质数
        }
        for(int j = 1;j <= cnt && i * a[j] < maxn;j++) {
            v[i * a[j]] = 1;//标记为合数
            if(i % a[j] == 0)break;//要是到了最小质因子就退出循环
        }
    }
}

为什么可以用欧拉筛呢？

因为每个数要么就是质数 要么就是最小质因子的幂 要么就是不同的质因子的乘积（但是这个已经被前面的消去了

#pragma GCC optimize(2)

#include
#include
#include 
#include
#include 
#include 
#include
#include 

using namespace std;

typedef long long ll;

const int maxn = 8e7 + 7;
const ll mod = 1ll << 32;

int a[5000000],cnt;
int v[maxn];

void getprime() {
    for(int i = 2;i < maxn;i++) {
        if(v[i] == 0) {//是质数
            v[i] = i;a[++cnt] = i;//a数组记录质数,v[i]也记录一笔
        }
        for(int j = 1;j <= cnt && i * a[j] < maxn;j++) {
            v[i * a[j]] = 1;//标记为合数
            if(i % a[j] == 0)break;//要是到了最小质因子就退出循环
        }
    }
}

ll qpow(ll x,ll n) {
    ll res = 1;
    while(n) {
        if(n & 1) res = res * x % mod;
        x = x * x % mod;
        n >>= 1;
    }
    return res;
}

ll gcd(ll n,ll m) {
    return m == 0 ? n : gcd(m,n % m);//最大公约数
}

int main() {
    getprime();//筛出所有素数存在a数组中
    ll n,A,B;scanf("%lld%lld%lld",&n,&A,&B);
    for(int i = 2;i <= n;i++) {
        v[i] = 0;//提前置零
    }
    
    for(int i = 1;i <= cnt;i++) {
        ll now = a[i];
        while(now <= n) {
            v[now] = i;//记录当前祖宗素数的下标（祖宗是指的底数）
            now = now * a[i];
        }//所有素数的素数倍
    }
    
    for(int i = 2;i <= n;i++) {
        if(v[i]) {//合数已被消去，没有鸡喙进入循环
            A = (A * a[v[i]] % mod + B) % mod;
        }
    }
    printf("%lld\n",A);
    return 0;
}

偷偷送清凉~(●ˇ∀ˇ●)