K近邻学习-距离计算补充-带你分析鸢尾花数据
一.K近邻(k-NN)理论介绍
这是一个简单的学习学习方法,易于理解,属于监督学习,同时也是懒惰学习的著名代表。
对于简单的数据分析,不涉及到很多的特征时候,k近邻算法有着突出的表现,比较适合分类任务。
它的工作机制很简单:给定测试样本,基于某种距离度量找出训练集中与其最靠近的k个训练样本,然后基于这k个样本的信息进行预测。在分类的任务中使用投票法(即选择这k个样本出现最多的类别标记作为预测结果),在回归任务中使用平均法(把这k个样本的实际值输出标记的平均值作为预测结果)。更近一步深入的话,可以基于距离的远近进行加权平均或加权投票,距离越近样本的权重越大。
二.形象解释
k-NN 算法最简单的版本只考虑一个最近邻,也就是与我们想要预测的数据点最近的训练
数据点。预测结果就是这个训练数据点的已知输出。

我们用圆圈表示0类,三角形表示 1类。新加入的数据(在我们训练集之外的数据)用五角星表示,五角星的颜色表示他们的预测结果。k为1时五角星的类别是离他最近样本的类别。
除了仅考虑最近邻,我还可以考虑任意个k 个邻居。这也是 k 近邻算法名字的来历。
在考虑多于一个邻居的情况时,我们用“投票法”来指定预测结果。也就是说对
于每个测试点,我们数一数多少个邻居属于类别 0,多少个邻居属于类别 1。然后将出现
次数更多的类别(也就是 k 个近邻中占多数的类别)作为预测结果。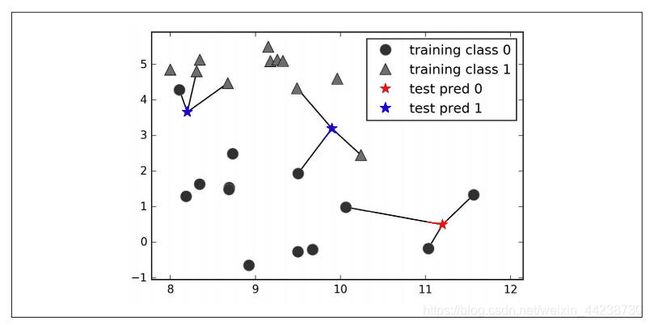
和上面一样,预测结果可以从五角星的颜色看出。你可以发现,左上角新数据点的预测结
果与只用一个邻居时的预测结果不同。
三.python代码实现
下面这段代码实现起来很短。因为python的库将这种模型封装的极为简单,你可以不用知道其原理就可以直接应用和学习。我们现在具体先看看我们的这种算法到底好不好用,其余的方面我们稍后再做讨论。
from sklearn.datasets import load_iris
#从sklearn的datasets导入鸢尾花的数据
from sklearn.model_selection import train_test_split
#导入的train_test_split方法用来打乱数据的顺序,返回有训练数据和测试数据集。比例为4:1
from sklearn.neighbors import KNeighborsClassifier
#导入k近邻分类模型的类
import numpy as np
X_new=np.array([[5,2.9,1,0.2]])
# scikit-learn输入数据必须是二维数组,我们必须遵守这个规则
knn=KNeighborsClassifier(n_neighbors=1)
#实例化学习模型
iris_dataset = load_iris()
#得到数据集
X_train, X_test, y_train, y_test = train_test_split(
iris_dataset['data'], iris_dataset['target'], random_state=0)
#利用train_test_split得到训练数据和测试数据集,X表示样本输入,y表示样本的标签
knn.fit(X_train,y_train)
#就这么简单的一句即可完成模型的训练,fit方法回对knn进行修改返回
predition =knn.predict(X_new)
#利用模型进行预测
print(predition)
# 打印出类别
print(iris_dataset['target_names'][predition])
# 完整的打印出类别字符串
# ----------开始评估模型是否准确
y_pred=knn.predict(X_test)
# 返回的是测试数据的预测结果
print(np.mean(y_pred==y_test))
# 打印出预测精度
print(knn.score(X_test,y_test))
# 用knn的score方法计算精度,与上面的方法是一样的
最后我们得到的预测准确率约为97%,说明k近邻学习模型在鸢尾花的分类上表现得较为出色。对于代码中设置参数时我们设置为了1,就是最简单的k近邻模型。你可以设置其它数字,在实际中这个数字取3-5一般能获得比较好的学习效果。
三.如何计算距离
1.数值距离
我们一直在说距离最近,那么这个距离是如何计算的呢。距离计算的方式有很多种,代码里面的knn你也可以设置距离计算的方式,一般默认为欧氏距离。大多数情况下它的表现都比较优良。
好的,正文开始了!
上面我们训练数据用的是鸢尾花的数据,输入的特征都是一些数值型的数据。鸢尾花的输入数据有四个特征,依次为花萼的长度,花萼的宽度,花瓣的长度,花瓣的宽度。简单点,假设我们现在又5组鸢尾花的数据。对应的类别我们也是知道的,简单起见,假设有正类和反类之分。用1 和 0 表示
[ 5.1 3.5 1.4 0.3]-----1
[ 4.9 3. 01.4 0.5]-----1
[ 4.7 3.2 1.3 0.1]-----0
[ 4.6 3.1 1.5 0.4]-----1
[ 5.0 3.6 1.4 0.2]-----0
好的现在新增加了一个数据,我们要预测这个数据是正类还是反类。
[4.8,2.6,1.6,0.5]
我们要找最近的距离,预测数据和哪个样本最近,我们就认为他是哪个类别。距离计算时我们一般用闵可夫斯基距离
(Xiu表示第i个本的第u个特征值。)p需要大于等一,p=2时就是我们前面所说的欧氏距离,p=1时我们称为曼哈顿距离。p还可以取其他值,我们视实际情况而定。
一般情况下我们用欧氏距离,读者可以自己利用这个公式计算一下,我们需要预测的数据和哪个样本的距离最接近,它的类别是什么。可以评论区告诉我
2.非数值距离
对于一些不是数值类型的距离我们应该如何去计算。现实生活当中我们经常会遇见一些非数值的特征。比如判断一个西瓜是不是甜西瓜时,我们把西瓜的拍打声作为一个特征,特征值有:浑重,清脆,浊响。这个时候我们应该如何去计算样本之间的距离呢
其中一种常用的计算方法时VDM,我们暂且只介绍这种方法,如果你有兴趣可以查阅资料看看其他的方法。
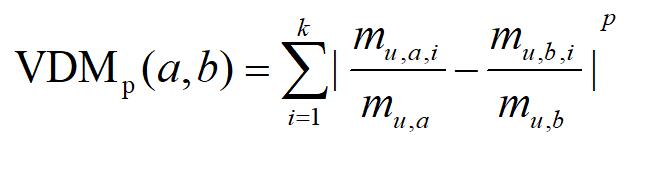
Mu,a表示在属性u上取值为a的样本数,Mu,a,i表示在第i个样本所在的类别中,在属性u上取值为a的样本个数。
2.非数值距离和数值距离
在实际的学习任务中,我们学习的样本大多都含有数值特征和非数值特征,我们一般将上面所说的距离加起来如下:
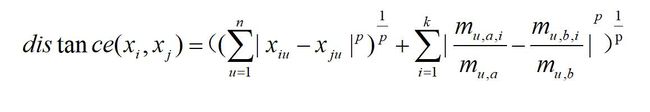
当样本空间的属性重要程度不同时,我们可以采取加权距离,这里不再详细的叙述。
补充:
小小补充一下,上面所说的所有的距离都是我们认为规定的。在不少的现实任务中,有必要基于数据样本来确定合适的距离计算公式,这也是一个学习模型,距离度量学习。本文章不再详细叙述,有兴趣可以查阅资料。
四.k近邻的优点、缺点和参数
一般来说,KNeighbors 分类器有 2 个重要参数:邻居个数与数据点之间距离的度量方法。在实践中,使用较小的邻居个数(比如 3 个或 5 个)往往可以得到比较好的结果,但你应该调节这个参数。默认使用欧式距离,它在许多情况下的效果都很好。参数过小容易发生过拟合现象,参数过大模型过于简单,无法准确预测数据。
k-NN 的优点之一就是模型很容易理解,通常不需要过多调节就可以得到不错的性能。在考虑使用更高级的技术之前,尝试此算法是一种很好的基准方法。构建最近邻模型的速度通常很快,但如果训练集很大(特征数很多或者样本数很大),预测速度可能会比较慢。使用 k-NN 算法时,对数据进行预处理是很重要的。这一算法对于有很多特征(几百或更多)的数据集往往效果不好,对于大多数特征的大多数取值都为 0 的数据集(所谓的稀疏数据集)来说,这一算法的效果尤其不好。
虽然 k 近邻算法很容易理解,但由于预测速度慢且不能处理具有很多特征的数据集,所以在实践中往往不会用到。