用JavaScript玩转计算机图形学(一)光线追踪入门

参考： http://www.cnblogs.com/miloyip/archive/2010/03/29/1698953.html

系列简介

记得小时候读过一本关于计算机图形学(computer graphics, CG)的入门书，从此就爱上了CG。本系列希望，采用很多人认识的JavaScript语言去分享CG，令更多人有机会接触，并爱上CG。

本系列的特点之一，是读者能在浏览器里直接执行代码，也可重覆修改代码测试。透过这种互动，也许能更深刻体会内容。读者只要懂得JavaScript(因为JavaScript很简单，学过Java/C/C++/C#之类的语言也应没问题)和一点点线性代数(linear algebra)就可以了。

笔者在大学期间并没有修读CG课程，虽然看过相关书籍，始终未亲手做过全域光照的渲染器，本文也作为个人的学习分享。此外，笔者也差不多十年没接触JavaScript，希望各位不吝赐教。

本文简介

多数程序员听到3D CG，就会联想到Direct3D、OpenGL等API。事实上，这些流行的API主要为实时渲染(real-time rendering)而设，一般采用光栅化(rasterization)方式，渲染大量的三角形(或其他几何图元种类(primitive types))。这种基于光栅化的渲染系统，只支持局部光照(local illumination)。换句话说，渲染几何图形的一个像素时，光照计算只能取得该像素的资讯，而不能访问其他几何图形资讯。理论上，阴影(shadow)、反射(reflection)、折射(refraction)等为全局光照(global illumination)效果，实际上，栅格化渲染系统可以使用预处理(如阴影贴图(shadow mapping)、环境贴图(environment mapping))去模拟这些效果。

全局光照计算量大，一般也没有特殊硬件加速(通常只使用CPU而非GPU)，所以只适合离线渲染(offline rendering)，例如3D Studio Max、Maya等工具。其中一个支持全局光照的方法，称为光线追踪(ray tracing)。光线追踪能简单直接地支持阴影、反射、折射，实现起来亦非常容易。本文的例子里，只用了数十行JavaScript代码(除canvas外不需要其他特殊插件和库)，就能实现一个支持反射的光线追踪渲染器。光线追踪可以用来学习很多计算机图形学的课题，也许比学习Direct3D/OpenGL更容易。现在，先介绍点理论吧。

光线追踪

光栅化渲染，简单地说，就是把大量三角形画到屏幕上。当中会采用深度缓冲(depth buffer, z-buffer)，来解决多个三角形重叠时的前后问题。三角形数目影响效能，但三角形在屏幕上的总面积才是主要瓶颈。

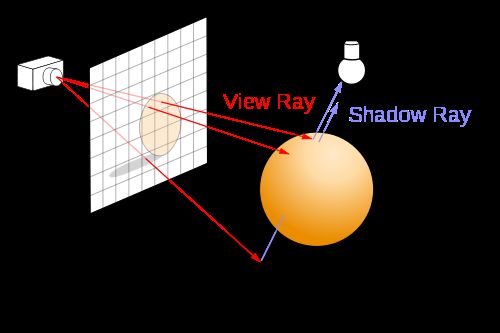
光线追踪，简单地说，就是从摄影机的位置，通过影像平面上的像素位置(比较正确的说法是取样(sampling)位置)，发射一束光线到场景，求光线和几何图形间最近的交点，再求该交点的著色。如果该交点的材质是反射性的，可以在该交点向反射方向继续追踪。光线追踪除了容易支持一些全局光照效果外，亦不局限于三角形作为几何图形的单位。任何几何图形，能与一束光线计算交点(intersection point)，就能支持。

上图(來源)显示了光线追踪的基本方式。要计算一点是否在阴影之内，也只须发射一束光线到光源，检测中间有没有障碍物而已。不过光源和阴影留待下回分解。

初试画板

光线追踪的输出只是一个影像(image)，所谓影像，就是二维颜色数组。

要在浏览器内，用JavaScript生成一个影像，目前可以使用HTML 5的。但现时Internet Explorer(直至版本8)还不支持，其他浏览器如Chrome、Firefox、Opera等就可以。

以下是一个简单的实验，把每个象素填入颜色，左至右越来越红，上至下越来越绿。

Run

左邊的canvas定義如下: < canvas width = "256" height = "256" id = "testCanvas" > canvas > 修改代码试试看 把第三个pixels[i++] = 0 改为255 (即蓝色全开) 把第四个pixels[i++] = 255 改为128 (alpha=128) 可以只修改两个for循环里面的代码，画一个国际象棋棋盘么?

这实验说明，从canvas取得的影像资料canvas.getImageData(...).data是个一维数组，该数组每四个元素代表一个象素(按红, 绿, 蓝, alpha排列)，这些象素在影像中从上至下、左至右排列。

解决实验平台的技术问题后，可开始从基础类别开始实现。

基础类

笔者使用基于物件(object-based)的方式编写JavaScript。

三维向量

三维向量(3D vector)可谓CG里最常用型别了。这里三维向量用Vector3类实现，用(x, y, z)表示。 Vector3亦用来表示空间中的点(point)，而不另建类。先看代码：

Vector3 = function (x, y, z) { this .x = x; this .y = y; this .z = z; };

Vector3.prototype = {
    copy : function () { return new Vector3( this .x, this .y, this .z); },
    length : function () { return Math.sqrt( this .x * this .x + this .y * this .y + this .z * this .z); },
    sqrLength : function () { return this .x * this .x + this .y * this .y + this .z * this .z; },
    normalize : function () { var inv = 1/ this .length(); return new Vector3( this .x * inv, this .y * inv, this .z * inv); },
    negate : function () { return new Vector3(- this .x, - this .y, - this .z); },
    add : function (v) { return new Vector3( this .x + v.x, this .y + v.y, this .z + v.z); },
    subtract : function (v) { return new Vector3( this .x - v.x, this .y - v.y, this .z - v.z); },
    multiply : function (f) { return new Vector3( this .x * f, this .y * f, this .z * f); },
    divide : function (f) { var invf = 1/f; return new Vector3( this .x * invf, this .y * invf, this .z * invf); },
    dot : function (v) { return this .x * v.x + this .y * v.y + this .z * v.z; },
    cross : function (v) { return new Vector3(- this .z * v.y + this .y * v.z, this .z * v.x - this .x * v.z, - this .y * v.x + this .x * v.y); }
};

Vector3.zero = new Vector3(0, 0, 0);

这些类方法(如normalize、negate、add等)，如果传回Vector3类对象，都会传回一个新建构的Vector3。这些三维向量的功能很简单，不在此详述。注意multiply和divide是与纯量(scalar)相乘和相除。

Vector3.zero用作常量，避免每次重新构建。值得一提，这些常量必需在prototype设定之后才能定义。

光线

所谓光线(ray)，从一点向某方向发射也。数学上可用参数函数(parametric function)表示：

当中，o即发谢起点(origin)，d为方向。在本文的例子里，都假设d为单位向量(unit vector)，因此t为距离。实现如下：

Ray3 = function (origin, direction) { this .origin = origin; this .direction = direction; }

Ray3.prototype = {
    getPoint : function (t) { return this .origin.add( this .direction.multiply(t)); }
};

球体

球体(sphere)是其中一个最简单的立体几何图形。这里只考虑球体的表面(surface)，中心点为c、半径为r的球体表面可用等式(equation)表示：

如前文所述，需要计算光线和球体的最近交点。只要把光线x = r(t)代入球体等式，把该等式求解就是交点。为简化方程，设v=o - c，则:

因为d为单位向量，所以二次方的系数可以消去。 t的二次方程式的解为

若根号内为负数，即相交不发生。另外，由于这里只需要取最近的交点，因此正负号只需取负号。代码实现如下：

Sphere = function (center, radius) { this .center = center; this .radius = radius; };

Sphere.prototype = {
    copy : function () { return new Sphere( this .center.copy(), this .radius.copy()); },

    initialize : function () {
        this .sqrRadius = this .radius * this .radius;
    },

    intersect : function (ray) {
        var v = ray.origin.subtract( this .center);
        var a0 = v.sqrLength() - this .sqrRadius;
        var DdotV = ray.direction.dot(v);

        if (DdotV <= 0) {
            var discr = DdotV * DdotV - a0;
            if (discr >= 0) {
                var result = new IntersectResult();
                result.geometry = this ;
                result.distance = -DdotV - Math.sqrt(discr);
                result.position = ray.getPoint(result.distance);
                result.normal = result.position.subtract( this .center).normalize();
                return result;
            }
        }

        return IntersectResult.noHit;
    }
};

实现代码时，尽快用最少的运算剔除没相交的情况(Math.sqrt是比较慢的函数)。另外，预计算了球体半径r的平方，此为一个优化。

这里用到一个IntersectResult类，这个类只用来记录交点的几何物件(geometry)、距离(distance)、位置(position)和法向量(normal)。 IntersectResult.noHit的geometry为null，代表光线没有和任何几何物件相交。

IntersectResult = function () {
    this .geometry = null ;
    this .distance = 0;
    this .position = Vector3.zero;
    this .normal = Vector3.zero;
};

IntersectResult.noHit = new IntersectResult();

摄影机

摄影机在光线追踪系统里，负责把影像的取样位置，生成一束光线。

由于影像的大小是可变的(多少像素宽x多少像素高)，为方便计算，这里设定一个统一的取样座标(sx, sy)，以左下角为(0,0)，右上角为(1 ,1)。

从数学角度来说，摄影机透过投影(projection)，把三维空间投射到二维空间上。常见的投影有正投影(orthographic projection)、透视投影(perspective projection)等等。这里首先实现透视投影。 ]]>

透视摄影机

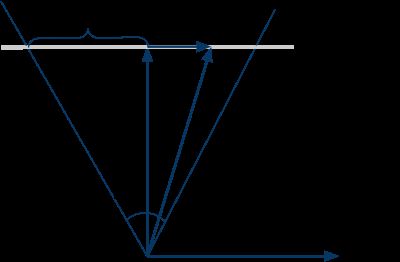
透视摄影机比较像肉眼和真实摄影机的原理，能表现远小近大的观察方式。透视投影从视点(view point/eye position)，向某个方向观察场景，观察的角度范围称为视野(field of view, FOV)。除了定义观察的向前(forward)是那个方向，还需要定义在影像平面中，何谓上下和左右。为简单起见，暂时不考虑宽高不同的影像，FOV同时代表水平和垂直方向的视野角度。

上图显示，从摄影机上方显示的几个参数。 forward和right分别是向前和向右的单位向量。

因为视点是固定的，光线的起点不变。要生成光线，只须用取样座标(sx, sy)计算其方向d。留意FOV和s的关系为：

把sx从[0, 1]映射到[-1,1]，就可以用right向量和s，来计算r向量，代码如下:

PerspectiveCamera = function (eye, front, up, fov) { this .eye = eye; this .front = front; this .refUp = up; this .fov = fov; };

PerspectiveCamera.prototype = {
    initialize : function () {
        this .right = this .front.cross( this .refUp);
        this .up = this .right.cross( this .front);
        this .fovScale = Math.tan( this .fov * 0.5 * Math.PI / 180) * 2;
    },

    generateRay : function (x, y) {
        var r = this .right.multiply((x - 0.5) * this .fovScale);
        var u = this .up.multiply((y - 0.5) * this .fovScale);
        return new Ray3( this .eye, this .front.add(r).add(u).normalize());
    }
};

代码中fov为度数，转为弧度才能使用Math.tan()。另外，fovScale预先乘了2，因为sx映射到[-1,1]每次都要乘以2。 sy和sx的做法一样，把两个在影像平面的向量，加上forward向量，就成为光线方向d。因之后的计算需要，最后把d变成单位向量。

渲染测试

写了Vector3、Ray3、Sphere、IntersectResult、Camera五个类之后，终于可以开始渲染一点东西出来！

基本的做法是遍历影像的取样座标(sx, sy)，用Camera把(sx, sy)转为Ray3，和场景(例如Sphere)计算最近交点，把该交点的属性转为颜色，写入影像的相对位置里。

把不同的属性渲染出来，是CG编程里经常用的测试和调试手法。笔者也是用此方法，修正了一些错误。

渲染深度

深度(depth)就是从IntersectResult取得最近相交点的距离，因深度的范围是从零至无限，为了把它显示出来，可以把它的一个区间映射到灰阶。这里用[0, maxDepth]映射至[255, 0]，即深度0的像素为白色，深度达maxDepth的像素为黑色。

// renderDepth.htm
function renderDepth(canvas, scene, camera, maxDepth) {
    // 从canvas取得imgdata和pixels，跟之前的代码一样
    // ...

    scene.initialize();
    camera.initialize();

    var i = 0;
    for ( var y = 0; y < h; y++) {
        var sy = 1 - y / h;
        for ( var x = 0; x < w; x++) {
            var sx = x / w;
            var ray = camera.generateRay(sx, sy);
            var result = scene.intersect(ray);
            if (result.geometry) {
                var depth = 255 - Math.min((result.distance / maxDepth) * 255, 255);
                pixels[i    ] = depth;
                pixels[i + 1] = depth;
                pixels[i + 2] = depth;
                pixels[i + 3] = 255;
            }
            i += 4;
        }
    }

    ctx.putImageData(imgdata, 0, 0);
}

Run

这里的观看方向是，正X轴向右，正Y轴向上，正Z轴向后。 修改代码试试看 改变球体的位置 改变球体的半径 改变fov(PerspectiveCamera最后的参数) 改变maxDepth(renderDepth最后的参数) 改变摄影机的方向，例如向左转一点点(记得要是单位向量啊!可以用new Vector(...).normalize())

渲染法向量

相交测试也计算了几何物件在相交位置的法向量，这里也可把它视觉化。法向量是一个单位向量，其每个元素的范围是[-1, 1]。把单位向量映射到颜色的常用方法为，把(x, y, z)映射至(r, g, b)，范围从[-1, 1]映射至[0, 255]。

// renderNormal.htm
function renderNormal(canvas, scene, camera) {
    // ...
            if (result.geometry) {
                pixels[i    ] = (result.normal.x + 1) * 128;
                pixels[i + 1] = (result.normal.y + 1) * 128;
                pixels[i + 2] = (result.normal.z + 1) * 128;
                pixels[i + 3] = 255;
            }
    // ...
}

Run

球体上方的法向量是接近(0, 1, 0)，所以是浅绿色(0.5, 1, 0.5)。 修改代码试试看 从球体的正上方往下看

材质

渲染深度和法向量只为测试和调试，要显示物件的"真实"颜色，需要定义该交点向某方向(如往视点的方向)发出的光的颜色，称之为几个图形的材质(material )。

材质的接口为function sample(ray, posiiton, normal) ，传回颜色Color的对象。这是个极简陋的接口，临时做一些效果出来，有机会再详谈。

颜色

颜色在CG里最简单是用红、绿、蓝三个通道(color channel)。为实现简单的Phong材质，还加入了对颜色的简单操作。

Color = function (r, g, b) { this .r = r; this .g = g; this .b = b };

Color.prototype = {
    copy : function () { return new Color( this .r, this .g, this .b); },
    add : function (c) { return new Color( this .r + c.r, this .g + c.g, this .b + c.b); },
    multiply : function (s) { return new Color( this .r * s, this .g * s, this .b * s); },
    modulate : function (c) { return new Color( this .r * c.r, this .g * c.g, this .b * c.b); }
};

Color.black = new Color(0, 0, 0);
Color.white = new Color(1, 1, 1);
Color.red = new Color(1, 0, 0);
Color.green = new Color(0, 1, 0);
Color.blue = new Color(0, 0, 1);

这Color类很像Vector3类，值得留意的是，颜色有调制(modulate)操作，其意义为两个颜色中每个颜色通道相乘。

格子材质

CG世界里，国际象棋棋盘是最常见的测试用纹理(texture)。这里不考虑纹理贴图(texture mapping)的问题，只凭(x, z)坐标计算某位置发出黑色或白色的光(黑色的光不叫光吧，哈哈)。

CheckerMaterial = function (scale, reflectiveness) { this .scale = scale; this .reflectiveness = reflectiveness; };

CheckerMaterial.prototype = {
    sample : function (ray, position, normal) {
        return Math.abs((Math.floor(position.x * 0.1) + Math.floor(position.z * this .scale)) % 2) < 1 ? Color.black : Color.white;
    }
};

代码中scale的意义为1坐标单位有多少个格子，例如scale=0.1即一个格子的大小为10x10。

Phong材质

这里实现简单的Phong材质，因为未有光源系统，只用全域变量设置一个临时的光源方向，并只计算漫射(diffuse)和镜射(specular)。

PhongMaterial = function (diffuse, specular, shininess, reflectiveness) {
    this .diffuse = diffuse;
    this .specular = specular;
    this .shininess = shininess;
    this .reflectiveness = reflectiveness;
};

// global temp
var lightDir = new Vector3(1, 1, 1).normalize();
var lightColor = Color.white;

PhongMaterial.prototype = {
    sample: function (ray, position, normal) {
        var NdotL = normal.dot(lightDir);
        var H = (lightDir.subtract(ray.direction)).normalize();
        var NdotH = normal.dot(H);
        var diffuseTerm = this .diffuse.multiply(Math.max(NdotL, 0));
        var specularTerm = this .specular.multiply(Math.pow(Math.max(NdotH, 0), this .shininess));
        return lightColor.modulate(diffuseTerm.add(specularTerm));
    }
};

Phong的内容不在此述。

渲染材质

修改之前的渲染代码，当碰到相交时，就向几何对象取得material属性，并调用sample方法函数取得颜色。

// rayTrace.htm
function rayTrace(canvas, scene, camera) {
    // ...
            if (result.geometry) {
                var color = result.geometry.material.sample(ray, result.position, result.normal);
                pixels[i] = color.r * 255;
                pixels[i + 1] = color.g * 255;
                pixels[i + 2] = color.b * 255;
                pixels[i + 3] = 255;
            }
    // ...
}

Run

修改代码试试看 改变fov，有了格子地板效果应该很明显 改变CheckerMaterial的scale 把原来红色的球改为绿色 把原来红色的球改为黄色 改变shininess(PhongMaterial最后一个参数)

多个几何物件

只渲染一个几何物件太乏味，这节再加入一个无限平面，和介绍如何组合多个几何物件。

平面

一个(无限)平面(Plane)在数学上可用等式定义:

n为平面的法向量，d为空间原点至平面的最短距离。光线和平面的相交计算很简单，这里不详述了。

Plane = function (normal, d) { this .normal = normal; this .d = d; };

Plane.prototype = {
    copy : function () { return new plane( this .normal.copy(), this .d); },

    initialize : function () {
        this .position = this .normal.multiply( this .d);
    },

    intersect : function (ray) {
        var a = ray.direction.dot( this .normal);
        if (a >= 0)
            return IntersectResult.noHit;

        var b = this .normal.dot(ray.origin.subtract( this .position));
        var result = new IntersectResult();
        result.geometry = this ;
        result.distance = -b / a;
        result.position = ray.getPoint(result.distance);
        result.normal = this .normal;
        return result;
    }
};

并集

把多个几何物件结合起来，可以使用集(set)的概念。这里最容易实现的操作，就是并集(union)，即光线要找到一组几个图形的最近交点。无需改其他代码，只加入一个Union类就可以：

Union = function (geometries) { this .geometries = geometries; };

Union.prototype = {
    initialize: function () {
        for ( var i in this .geometries)
            this .geometries[i].initialize();
    },

    intersect: function (ray) {
        var minDistance = Infinity;
        var minResult = IntersectResult.noHit;
        for ( var i in this .geometries) {
            var result = this .geometries[i].intersect(ray);
            if (result.geometry && result.distance < minDistance) {
                minDistance = result.distance;
                minResult = result;
            }
        }
        return minResult;
    }
};

可以看到，这里利用Javascript的多型(polymorphism)的特性，完全不用修改原来的代码，就可以扩展功能。

如前所述，这里只考虑几何几何图形的表面。如果考虑几何图形是实心的，就可以用构造实体几何(constructive solid geometry, CSG)方法，提供并集、交集、补集等操作。容后再谈。

反射

以上实现的，也只是局部照明。只要再加入一点点代码，就可以实现反射。

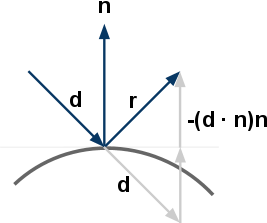
下图说明反射向量的计算方法:

把d投射到n上(因n是单位向量，只需要点乘即可)，就可以计算d在n上的长度，把d减去这长度两倍的法向量，就是反射向量r。数学上可写成:

一般材质并非完全反射(镜子除外)，因此这里为材质加上一个反射度(reflectiveness)的属性。反射的功能很简单，只要在碰到反射度非零的材质，就继续向反射方向追踪，并把结果按反射度来混合。例如一个材质的反射度为25%，则它传回的颜色是75%本身颜色，加上25%反射传回来的颜色。

另外，不断反射会做成大量的运算，甚至乎永远不能停止(考虑摄影机在两个镜子中间)。因此要限制反射的次数。含反射功能的光线追踪代码如下：

function rayTraceRecursive(scene, ray, maxReflect) {
    var result = scene.intersect(ray);

    if (result.geometry) {
        var reflectiveness = result.geometry.material.reflectiveness;
        var color = result.geometry.material.sample(ray, result.position, result.normal);
        color = color.multiply(1 - reflectiveness);

        if (reflectiveness > 0 && maxReflect > 0) {
            var r = result.normal.multiply(-2 * result.normal.dot(ray.direction)).add(ray.direction);
            ray = new Ray3(result.position, r);
            var reflectedColor = rayTraceRecursive(scene, ray, maxReflect - 1);
            color = color.add(reflectedColor.multiply(reflectiveness));
        }
        return color;
    }
    else
        return Color.black;
}

function rayTraceReflection(canvas, scene, camera, maxReflect) {
    // 从canvas取得imgdata和pixels，跟之前的代码一样
    // ...

    scene.initialize();
    camera.initialize();

    var i = 0;
    for ( var y = 0; y < h; y++) {
        var sy = 1 - y / h;
        for ( var x = 0; x < w; x++) {
            var sx = x / w;
            var ray = camera.generateRay(sx, sy);
            var color = rayTraceRecursive(scene, ray, maxReflect);
            pixels[i++] = color.r * 255;
            pixels[i++] = color.g * 255;
            pixels[i++] = color.b * 255;
            pixels[i++] = 255;
        }
    }

    ctx.putImageData(imgdata, 0, 0);
}

Run

修改代码试试看 改变一个球的reflectiveness，试试0、1及之间的数值 改变maxReflect(rayTraceReflection最后一个参数) 加入更多的球体(可用for循环啊……不过小心渲染时间太长)

结语

能体会到计算机图形学的有趣之处么？百多行简单的JavaScript代码，就绘画出像真的影像，那种满足感实非笔墨所能形容。

本文实现了一个简单的光线追踪渲染器，支持球体、平面、Phong材质、格子材质、多重反射等功能。读者可以下载这组代码，加入不同的扩展，也可以尝试翻译做熟悉的编程语言。很多光线追踪用到的计算机图形技术，也可以应用到实时图形编程里，例如光源和材质的计算，基本上可以简易翻译做实时图形的著色器(shader)编程。

游戏里采用光栅化渲染技术已有二十年以上，这几年的硬件发展，使其他渲染方法也能用于实时应用。光线追踪和其他类似的方法，有个当今重要优点，就是能高度平行化。采样之间并没有依赖性，例如256x256=65536个采样，理论上，可使用65536个机器/核心独立执行追踪，那么完成时间只是最慢的一个取样所需的时间。

笔者希望继续撰写这系列，例如包括以下内容:

• 其他几何图形(长方体、柱体、三角形、曲面、高度场、等值面、……)
• 光源(方向光源、点光源、聚光灯、阴影、ambient occlusion)
• 材质(Phong-Blinn、Oren-Nayar、Torrance-Sparrow、折射、 Fresnel、BRDF、BSDF……)
• 纹理(纹理座标、采样、Perlin noise)
• 摄影机模型(正投射、全景、景深)
• 成像流程(渐进渲染、反锯齿、后期处理)
• 优化方法(场景剖分、低阶优化)
• 其他全局光照渲染方法

祈望得到大家的意见反馈。

参考

• Matt Pharr, Greg Humphreys, Physically Based Rendering, Morgan Kaufmann, 2004
• Wikipedia, Ray Tracing
• Slime, The JavaScript Raytracer
• SIGGRAPH HyperGraph Education Project, Ray Tracing

更新

• 2010年3月31日，网友HouSisong把本文代码以C++实现，并完全保留了原设计，代码可於他的博文下载。