树的分治-点分治

ps：太弱了，才刚学点分治，蒟蒻+=∞

作用

求一棵树上满足条件的节点二元组(u,v)个数，比较典型的是求dis(u,v)（dis表示距离）满足条件的(u,v)个数。

实现

对于上述问题，我们有一个初始想法，就是先随便挑选出一个节点ro作为根节点，然后计算以ro为中介点的(u,v)个数（利用排序等算法），之后递归处理ro的儿子，再处理ro的儿子的儿子，以此类推，就可以求出答案。

然而如果这是一条链，而ro又选成了链首或链尾，就会导致效率低下，时间复杂度退化为 O(n2) 。所以说，ro的选择很重要，但是要怎么选择？这里引入树的重心的概念：设MAX(x)表示x所有子树节点数的最大值，则树的重心ro满足MAX(ro)是所有MAX(x)中最小的。这个性质很强大，可以保证所有子树节点数不超过n/2！下面用反证法给出简单的证明：
设重心为ro，假设重心不能保证所有子树节点数不超过n/2，则必有一棵子树M节点数超过n/2，如图：

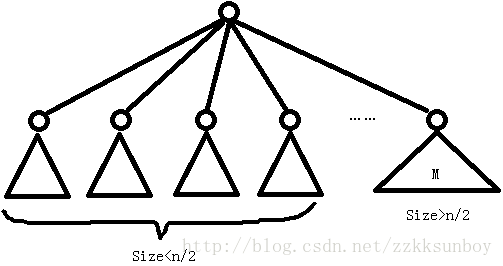
因为Size(M)大于n/2，所以其他子树加上ro的节点数肯定小于n/2，这时候莫不如选M，因为这样选MAX(M)=Size(M)-1＜MAX(ro)=Size(M)，所以ro不是重心，与题设矛盾。所以重心能保证所有子树节点数不超过n/2。

那么也就是说每次选重心，子树节点数都会/2，所以层数为log2(n)，而每层都会处理n次，所以点分治的效率为 O((n+T)∗log2(n)) ，T表示计算的复杂度。

模板

以POJ1741为例。
明显就是点分治。每次先求出重心，然后统计，先计算出当前树所有节点的距离，进行排序，然后统计满足的个数。然而这样是有重复的，重复就是子树的满足个数（子树内的节点满足是不符合以当前重心为中介点的）。最后减去重复就是答案。
还有另外一种做法，题解传送门。

#include
#include
#include
using namespace std;
const int maxn=10000;

int n,E,K,ans,son[2*maxn+5],nxt[2*maxn+5],w[2*maxn+5],lnk[maxn+5];
int ro,S,MAX[maxn+5],si[maxn+5],dep[maxn+5],now[maxn+5];
bool vis[maxn+5];

void Add(int x,int y,int z) {son[++E]=y;w[E]=z;nxt[E]=lnk[x];lnk[x]=E;}
void getro(int x,int fa) //获取重心
{
    si[x]=1;MAX[x]=0;
    for (int j=lnk[x];j;j=nxt[j])
        if (son[j]!=fa&&!vis[son[j]])
        {
            getro(son[j],x);
            si[x]+=si[son[j]];
            MAX[x]=max(MAX[x],si[son[j]]);
        }
    MAX[x]=max(MAX[x],S-si[x]);
    if (ro==-1||MAX[x]void getdep(int x,int fa) //获取距离
{
    now[++now[0]]=dep[x];
    for (int j=lnk[x];j;j=nxt[j])
        if (son[j]!=fa&&!vis[son[j]])
        {
            dep[son[j]]=dep[x]+w[j];
            getdep(son[j],x);
        }
}
int getsum(int x,int dis) //获取x节点子树的满足个数
{
    dep[x]=dis;now[0]=0;getdep(x,-1);
    sort(now+1,now+1+now[0]);
    int L=1,R=now[0],sum=0;
    while (Lif (now[L]+now[R]<=K) sum+=R-L,L++; else R--;
    return sum;
}
void getans(int x) //获取答案
{
    vis[x]=true;ans+=getsum(x,0);
    for (int j=lnk[x];j;j=nxt[j])
        if (!vis[son[j]])
        {
            ans-=getsum(son[j],w[j]); //减去重复
            ro=-1;S=si[son[j]];getro(son[j],x);
            getans(ro);
        }
}
int main()
{
    freopen("program.in","r",stdin);
    freopen("program.out","w",stdout);
    for (scanf("%d%d",&n,&K);n||K;scanf("%d%d",&n,&K))
    {
        memset(vis,0,sizeof(vis));memset(lnk,0,sizeof(lnk));E=0;ans=0;
        for (int i=1;i<=n-1;i++)
        {
            int x,y,z;scanf("%d%d%d",&x,&y,&z);
            Add(x,y,z);Add(y,x,z);
        }
        ro=-1;S=n;getro(1,-1);getans(ro);
        printf("%d\n",ans);
    }
    return 0;
}