CASS 第一章总结
本章目标
- 了解程序的本质
- 文本文件和二进制文件的区别
- 了解计算机体系结构
- 编译系统(预处理,编译,汇编,链接)
- 了解机器字长
- 知道指令集架构和微体系结构是什么
- 了解I/O设备(文件)
- 了解虚拟内存
- 衡量性能提升
前言
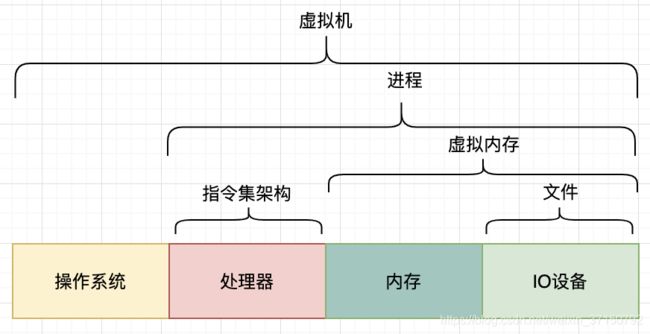
本章中, 我觉得最重要的知识就是理解下面的图片.
程序本质
程序大家都不陌生, 日常开发的写的代码都是程序中的一部分, 而程序在计算机中具体是怎么表示呢?
要想知道上面问题的答案, 必须知道程序的本质. 程序本质上就是字节序列. 而字节就是由0和1组成, 0和1 具体也叫做位, 8位等于1个字节. 所以特定的字节序列就组成了程序.
文本文件和二进制文件
文本文件和二进制文件本质上都是由字节序列组成, 但是文本文件要人可阅读, 二进制文件需要机器可阅读. 因此需要有字符和位的映射, 这种映射就是编码集, 编码集不光有一种, 存在了很多的编码集, 现在比较流行也最通用的就是UTF-8编码集.
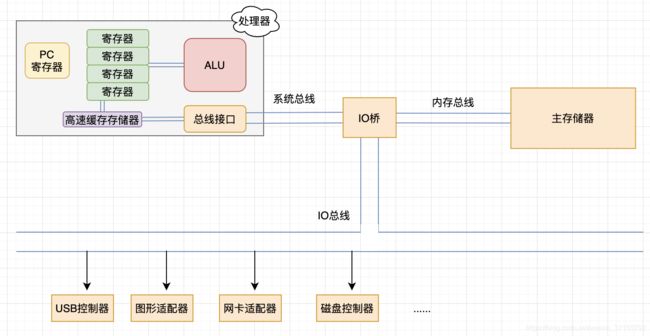
了解计算机体系架构
- ALU 处理逻辑单元 用于执行逻辑运算等
- 寄存器, 图中只画出了部分寄存器, 具体数量取决于微结构, 而微结构受限于指令集架构(下面会说到)
- PC寄存器 ALU当前指令的地址
- 高速存储寄存器, 图中只画了一块, 而实际上它是有层级结构.
- 总线接口, 处理器传输的数据全部都要经过总线接口
主存储器也就是平时大家说的内存, 或者运行时内存, 现在的内存普遍都4G,8G, 而且16G的也很常见了.
在IO总线上连接着一些灵活的设备, 他们非常方便更换, 比如鼠标, 键盘等. IO总线上的设备通过控制器或适配器与主板相连. 控制器和适配器的区别: 控制器常常在IO设备本身或主板的芯片组上. 适配器是插在主板插槽上的卡. 但是两者的功能都是为了传输数据.
编译系统
编译系统提供从源代码到可执行目标文件翻译的过程. 而源代码一般是较为高级的语言, 比如C语言,C++语言, 而可执行目标文件由机器语言组成, 机器语言是计算机能够直接读懂的语言, 有了机器语言就知道进行什么操作.
编译系统具体将源代码翻译为可执行目标文件的步骤可以列为四个阶段:
- 预处理阶段
- 编译阶段
- 汇编阶段
- 链接阶段
第一个阶段主要是将源代码中引用了外部文件以文本的形式进行替换, 比如#includestdio.h`中的内容直接替换到源代码中;
第二个阶段是将源代码翻译为汇编代码,这个阶段的输出结果还是文本文件;
第三个阶段将汇编代码翻译为机器语言指令, 这个阶段输出的结果是二进制文件, 该文件也叫可重定位目标程序;
第四个阶段将可重定位目标程序与使用到的类库的具体实现链接形成可执行目标文件.
可重定位目标程序和可执行目标文件是什么?
机器字长
在计算机中常常要在总线上传输数据, 而总线一次只能传输固定长度的字节, 这些字节称为字节块, 也就是字. 说计算机4字长意味着总线一次可以传输32位数据. 现在计算机大都是8字长, 一次可以传输64位.
指令集架构和微体系结构
指令集架构是一种标准, 它为上层提供了抽象性, 比如说add x y 指令是将x的值和y的值相加, 然后将数据存放在x的寄存器上. 而指令集架构就是由很多这样的指令构成, 它指定的是标准, 因此可以有不同的指令集架构的机器. 比如MacOS X 系统的指令集架构和Linux系统的指令集架构就不一样.
微体系结构又叫微架构, 它是处理器的具体实现, 底层由电子元器件组成.
举个例子来说: 你现在使用的是Windows系统,然后重新安装了一个Linux系统, 则是指令集架构发生了变化, 而微体系结构并没有改变.
了解文件
这里说的文件并不是存储在磁盘中的书籍, 电影. 而是指连接在IO总线上的IO设备, 比如鼠标, 键盘. 网卡甚至显示器. 这些IO设备可以认为是字节序列, 系统会通过一批Unix I/O的系统调用(运行在内核态的函数)与IO设备交互.
了解虚拟内存
虚拟内存为每个进程提供了一个非常大的虚拟空间. 让进程不用关心真实的物理内存是否够用, 真实的数据是存储在物理存储的那个部位. 处理器根据虚拟空间中的虚拟地址就能够定位到进程需要的数据.
每个进程的虚拟地址空间中的划分都有相同的数据结构, 保存代码和数据的区域, 运行时需要的堆内存区域等.(知道有划分的概念即可)
衡量性能提升
表示性能提升的方式有很多种, 但是比较直观的还是用 S = T o l d T n e w S = \frac {T_{old}}{T_{new}} S=TnewTold, 其中 T o l d T_{old} Told 是没有改变前操作需要的时间, 而 T n e w T_{new} Tnew 是改变之后操作需要的时间, 若 S = = 1 S == 1 S==1 , 则代表提升无效, 若 S > 0 S > 0 S>0, 则代表有提升效果, 若 S < 0 S < 0 S<0 , 则代表效果反而变坏了.
Amdahl 提出了一项定律来描述系统中部分性能提升对整体带来的效果.
Amdahl的公式: S = 1 ( 1 − a ) + a / k S = \frac {1}{(1-a) + a/k} S=(1−a)+a/k1
a a a 表示系统中没有提升前, 部分执行时间与总共执行时间的比例, 假设某部分需1h, 而整体需要2h, 则 a = 0.5 a = 0.5 a=0.5.
k k k 表示提升部分的比例, 假设原来10m/s, 提升以后是15m/s, 则 k = 1.5 k = 1.5 k=1.5
现在公式中的各部分已经理解了, 那么这个公式是怎么得出的呢? 就是基于刚开始提出的 S = T o l d T n e w S = \frac {T_{old}}{T_{new}} S=TnewTold, 下面推导下公式:
T 提 升 之 后 需 要 的 时 间 = T 未 提 升 部 分 需 要 的 时 间 + T 提 升 后 部 分 所 需 要 的 时 间 = ( 1 − a ) T o l d + ( a T o l d ) / k T_{提升之后需要的时间}=T_{未提升部分需要的时间}+T_{提升后部分所需要的时间}=(1-a)T_{old}+(aT_{old})/k T提升之后需要的时间=T未提升部分需要的时间+T提升后部分所需要的时间=(1−a)Told+(aTold)/k
根据上面的描述等出右边的公式: T n e w = ( 1 − a ) T o l d + ( a T o l d ) / k = T o l d [ ( 1 − a ) + a / k T_{new} = (1-a)T_{old} + (aT_{old})/k=T_{old}[(1-a)+a/k Tnew=(1−a)Told+(aTold)/k=Told[(1−a)+a/k
于是最后得出: S = T o l d T n e w = 1 ( 1 − a ) + a / k S=\frac {T_{old}}{T_{new}}=\frac 1{(1-a)+a/k} S=TnewTold=(1−a)+a/k1