编译原理:第五节
有限自动机
有限自动机定义与分类:
对语言的有穷描述的一种方法,识别方式,能够识别正则文法所定义的语言。分为确定的有限自动机(DFA)和非确定的有限自动机(NFA)。
DFA的定义:
一个确定的有限自动机M(DFA M)是一个五元组:
M = (Q,
Σ,f,q0,Z)
Q:状态的有限集合,每个集合为一个状态
Σ:输入字符的有限集合(有穷字母表),每个元素是一个输入字符
f:状态转移函数,是一个 Q×Σ 到Q的映射,q0∈Q
Z:M的终态集(接受状态集)
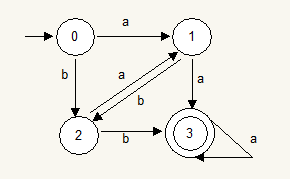
DFA的状态图表示:
设DFA:M = ({0,1,2,3},{a,b},f,0,{3} )
其中 f :f (0,a) = 1 f (0,b) = 2 f (1,a) = 3 f (1,b) = 2 f (2,b) = 3 f(2,a) = 1 f(3,a) = 3
状态图表示为:
其可接受的字符串有aa,aaa,bb,baa等等。DFA M可接受的字符串的全体称为M是别的语言,记做L(M)。
非确定有限自动机(NFA)的定义:
对上面的DFA稍加修改,使其在状态下的输入一字符的转换状态不是唯一的,而允许转换为多个状态,并允许不扫描字符就可转换状态,这样的有限状态机称为非确定的有限状态机(NFA)
一个非确定的有限自动机M(NFA M)是一个五元组:
M = (Q,Σ,f,q0,Z)
Q:状态的有限集合,每个集合为一个状态
Σ:输入字符的有限集合(有穷字母表),每个元素是一个输入字符
f:状态转移函数
Z:M的终态集(接受状态集)
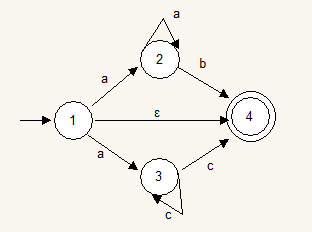
例如一个NFA:
DFA与NFA的等价:
定义1:
设 I ⊆ Q (Q为NFA M的状态集)定义 ε - closure(I)为:
若 q∈I ,则 q∈
ε - closure(I)
若q∈I,则对于任意q' ∈ f (q,ε),有q'∈ε - closure(I)
状态集ε - closure(I)称为状态集 I 的ε 闭包
例如:上图中:设 I = { 0 } ,则ε - closure(I)= ε - closure({1})= { 0,1,2,3,4}
定义2:
设NFA M = (Q,Σ,f,q0,Z)
若I ⊆ Q ,则定义Ia = ε - closure({p∈ f(q,a) | q∈ ε - closure(I)})
即Ia 是所有从 I的闭包出发,经过一条a弧而到达状态集的ε闭包
例如:上图中 设 I = { 0,1,2,3,4} 则 Ia = { 5 } Ib = { 5 }
定理:
对任何一个NFA M,都存在一个DFA M ’ ,使得 L(M) = L(M')
NFA转化为DFA:子集构造法
/**
输入:NFA M =(Q,Σ,f,q0,Z)
输出:DFA M'=(Q',Σ,f',q0',Z')
**/
1. 将Q'初始化为ε - closure(q0)= q'
2. while(存在状态集 x∈Q',任意a∈Σ,f'(x,a)没有定义){
置f'(x,a) = xa;
if(f'(x,a)∈Q'){
Q' = Q'∪{f'(x,a);
}
}
3. Z' = {K|k∈Q'且K∩Z≠空集}
4. 重命名Q'中的状态,并相应修改其他项
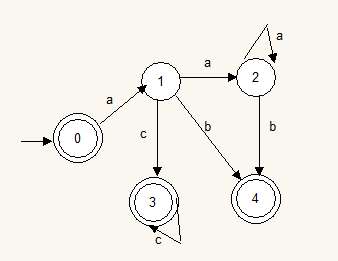
求转化后的DFA?
解:
I =
ε - closure({1})= { 1,4}
{1,4}a = {2,3} {1,4}b = Ø {1,4}c = Ø
{2,3}a = {2} {2,3}b = {4} {2,3}c = {3,4}
{2} a = {2} {2} b = {4} {2} c = Ø
{4} a = Ø {4} b = Ø {4} c = Ø
{3,4}a = Ø {3,4}b = Ø {3,4}c = {3,4}
其中包含终端4的集合有:{1,4} {4} {3,4} 其余为:{2,3} {2}
由此求得DFA的状态图表示为:
DFA的化简
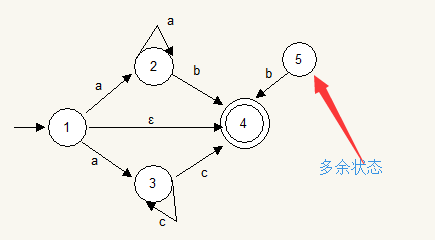
我们给出一个DFA,并不能保证其为最简形式,例如:
多余状态(无关状态):不在从开始到终结状态的路径上的状态
等价状态:设p,q ∈S ,若对任何w ∈Σ * , f (p,w) 与 f(q,w) 同时到达接收状态或拒绝状态,则称p,q等价