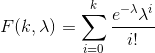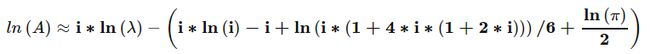大型Lambda的C# 泊松累积分布
目录
介绍
背景
使用代码
- 下载源8.7 KB
介绍
用Ramanujan的阶乘近似值计算C#中的泊松分布
背景
如果需要用于很大型Lambda的泊松累积分布函数,则可以使用此代码。
使用代码
泊松概率质量函数的公式为:
在C#中,可以将其计算为:
public double Cdf(long k)
{
var e = Math.Pow(Math.E, -_lambda);
long i = 0;
var sum = 0.0;
while (i <= k)
{
sum += e * Math.Pow(_lambda, i) / Factorial(i);
i++;
}
return sum;
}问题在于,随着k和_lambda(_lambda = λ)增加,分母都变得非常大,并且程序崩溃。这可以通过使用对数来解决。为简单起见,自然对数是用于:![]() 。计算中使用以下规则:
。计算中使用以下规则:
计算使用对数和Ramanujan的阶乘近似表示:
请在此处详细了解。
设置Math.Pow(_lambda, i) / Factorial(i)= (A) = (\frac{\lambda ^{i}}{i!})给出了
通过使用Ramanujan的阶乘近似,我们得到:
使用C#表示法并利用![]() ,我们得到:
,我们得到:
A = Math.Pow(e, i*ln(ℷ) -i*ln(i) + i - ln(i*(1 + 4*i*(1 + 2*i)))/6 - ln(π)/2))
可以在C#计算中使用此表达式,如以下代码所示:
var log6ThTail = Math.Log(i * (1 + 4 * i * (1 + 2 * i)))/6;
var lnN = i * Math.Log(_lambda) - (i * Math.Log(i) - i + log6ThTail + logPiDivTwo);
n = Math.Pow(Math.E, lnN - _lambda);这是代码:
using System;
namespace PoissonEvaluator
{
public class PoissonDistribution
{
private readonly double _lambda;
public PoissonDistribution(double lambda = 1.0)
{
_lambda = lambda;
}
public double Pmf(long k)
{
if (k > 170 || double.IsInfinity(Math.Pow(_lambda, k)))
{
var logLambda = k * Math.Log(_lambda) -
_lambda - (k * Math.Log(k) - k +
Math.Log(k * (1 + 4 * k * (1 + 2 * k))) / 6 +
Math.Log(Math.PI) / 2);
return Math.Pow(Math.E, logLambda);
}
return Math.Pow(Math.E, -_lambda) * Math.Pow(_lambda, k) / Factorial(k);
}
public double Cdf(long k)
{
long i = 0;
var sum = 0.0;
var infinityIsFound = false;
var eLambda = Math.Pow(Math.E, -_lambda);
var logPiDivTwo = Math.Log(Math.PI) / 2;
while (i <= k)
{
double n;
if (infinityIsFound)
{
var log6ThTail = Math.Log(i * (1 + 4 * i * (1 + 2 * i))) / 6;
var lnN = i * Math.Log(_lambda) - (i * Math.Log(i) - i +
log6ThTail + logPiDivTwo);
n = Math.Pow(Math.E, lnN - _lambda);
}
else
{
if (i > 170 || double.IsInfinity(Math.Pow(_lambda, i)))
{
infinityIsFound = true;
var log6ThTail = Math.Log
(i * (1 + 4 * i * (1 + 2 * i))) / 6;
var lnN = i * Math.Log(_lambda) -
(i * Math.Log(i) - i +
log6ThTail + logPiDivTwo);
n = Math.Pow(Math.E, lnN - _lambda);
}
else
{
n = eLambda * Math.Pow(_lambda, i) / Factorial(i);
}
}
sum += n;
i++;
}
return (sum > 1) ? 1.0 : sum;
}
public double Factorial(long k)
{
long count = k;
double factorial = 1;
while (count >= 1)
{
factorial = factorial * count;
count--;
}
return factorial;
}
}