poj2796--Feel Good(单调栈求区间问题)
题意:区间内数的总和 乘上 区间内的最小值 为心情值,求心情值的最大值
思路:虽然知道是单调栈但是想了好久都没想出来怎么用到单调栈,后来终于给我推出来了,我用图解的形式一步步告诉你
讲解之前先放上单调栈的概念,已经知道的可以忽略~
单调栈指栈中的元素从上往下看都是按一定的大小排下来的。所以一个元素进栈时要先让一些元素出栈才能再进站。
这里我用单调递增栈做个例子,即从栈顶往下看是越来越大的。
有一群数字2,9,4,7,3,10
栈为空,2进栈、
9要进栈,但是2比9小,故2先出栈,9再进栈。
4进栈,没问题,9比4大。
7要进栈,但是4比7小,故4出栈,9比7大,不必出栈,故7进栈。
3比7小,进栈
10要进栈,故3、7、9出栈,10进栈。
整个栈的变化为NULL->2->9->9,4->9,7->9,7,3->10
首先,对于这题,最重要的一点是用最小值表示区间,而不是用区间表示区间。
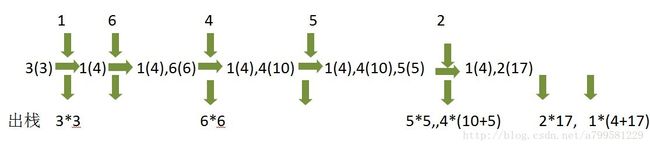
就拿3,1,6,4,5,2这个例子来讲,先放上图,在配上说明
3首先入栈,以3(3)表示,意为 当前以3为最小值的区间中的总和为3
随后要放入1,1比3要小,那么也就意味着 以3为最小值的区间已经结束了,因为3的左右都是比它要小的数字,所以无法再扩展出去,所以3要出栈,出栈时计算3*3,更新max,同时1入栈,表示为1(4),即以1为最小值的区间中的数的和为4.
然后再要放入6,6比1大,故直接放入,栈中表示为1(4),6(6),6(6)指以6为最小值的区间中的总和为6.
然后再放入4,因为6的左边是1,6又比4大,所以以6为最小值的区间已经结束,故6出栈,出栈时计算6*6,更新max,4入栈,为4(10)。
5入栈,栈中为1(4),4(10),5(5)。
再放入2,因为2比5小,5的区间已结束,5出栈,计算5*5. 5出栈后还有个4,4的区间范围是包括5那部分的,所以4出栈时要计算4*(10+5)。
现在所有数字都已经放过了。栈中还剩下1(4)和2(17)。这两个区间的好心情值还没算过,依次出栈,计算2*17,
然后1出栈,因为1是包括2的那部分的,所以计算1*(4+17)。
最终得知答案为4*(10+5)=60那次
#include
#include
#include
#define M 100005
using namespace std;
int a[M];
struct stack
{
int top,num[M],l[M]; //num指数字,l指它的最左端,sum指已经覆盖的值的总和
long long sum[M];
};
stack s;
int main()
{
int n,i,j,ll;
long long k;
cin>>n;
s.top=0; //初始化栈
long long max=-1,
int ansl,ansr; //作为答案的左端和右端
for(i=1;i<=n;i++)
{
scanf("%d",&a[i]);
k=0;
ll=i; //最左端暂定为它自己
while(s.top!=0&&s.num[s.top]>=a[i]) //如果非空并且栈顶端的值比它大,出栈
{
k+=s.sum[s.top]; //k保存出栈的sum的总和
ll=s.l[s.top]; //最左端变小(向左移动了)
if(k*s.num[s.top]>max) { max=k*s.num[s.top];ansl=s.l[s.top];ansr=i-1;} //最大值更新
s.top--;
}
s.sum[++s.top]=k+a[i]; //入栈
s.num[s.top]=a[i];
s.l[s.top]=ll;
}
//所有入栈操作已经完结,但是单调栈内元素的还未进行过与最大值的比较,一个个出栈
k=0;
while(s.top!=0)
{
k+=s.sum[s.top];
if(s.num[s.top]*k>max)
{
max=s.num[s.top]*k;
ansl=s.l[s.top];
ansr=n;
}
s.top--;
}
printf("%lld\n%d %d\n",ans,ansl,ansr); //记住lld
}