图的深度与广度遍历及最小生成树

上一篇文章讲了图的有关概念以及图的两种存储方式， 点击打开链接

接下来我们一起学习图的两种遍历及最小生成树的实现。

一、图的遍历

1、广度优先遍历（Breadth First Search, BFS）

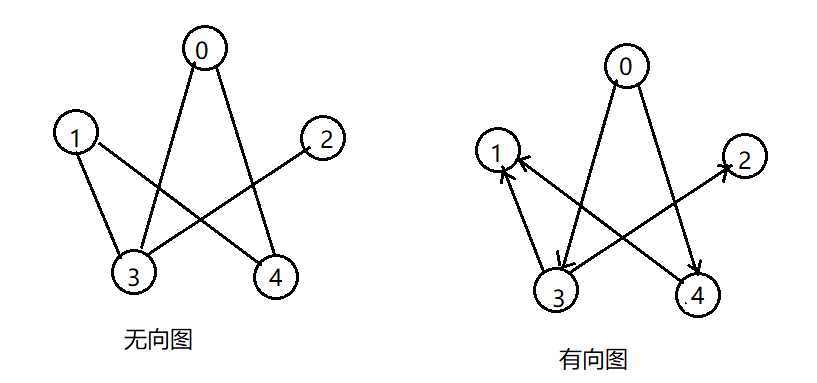
广度优先搜索类似于树的层序遍历，看一个例子：

假设我们都从节点0开始遍历，无向图遍历顺序为0,3,4,1,2,，有向图遍历顺序为0,3,4,1,2。

下面是实现的代码，需要借助队列来完成：

// 图的广度优先遍历 
	void BFS(const V& v)
	{
		queue q;
		//标记是否已经遍历，遍历过为true
		vector visited(_v.size(), false);
		size_t index = GetIndexOfV(v);
		q.push(index);
		_BFS(q, visited);

		//避免漏掉与其他顶点无关的点
		for (size_t i = 0; i < _v.size(); i++)
		{
			if (visited[i] == false)
			{
				q.push(i);
				_BFS(q, visited);
			}
		}
		cout << endl;
	}
       void _BFS(queue& q, vector& visited)
	{
		while (!q.empty())
		{
			size_t index = q.front();
			q.pop();
			if (visited[index] == true)
				continue;
			visited[index] = true;
			cout << _v[index] << " ";

			pNode pCur = _linkEdges[index];
			while (pCur)
			{
				if (visited[pCur->_dst] == false)
					q.push(pCur->_dst);
				pCur = pCur->_pNext;
			}
		}
	}

2、深度优先遍历

深度优先遍历相当于一条路走到黑的道理，还是上面的例子：

假设我们都从节点0开始遍历，无向图遍历顺序为0,3,1,4,2，有向图遍历顺序为0,3,1,2,4。

代码如下：

// 图的深度优先遍历 
	void DFS(const V& v)
	{
		size_t index = GetDevOfV(v);
		vector visited(_v.size(), false);
		_DFS(index, visited);

		for (size_t i = 0; i < _v.size(); i++)
		{
			if (visited[i] == false)
				_DFS(i, visited);
		}
		cout << endl;
	}
        void _DFS(int index, vector& visited)
	{
		cout << _v[index] << " ";
		visited[index] = true;

		pNode pCur = _linkEdges[index];
		while (pCur)
		{
			if (visited[pCur->_dst] == false)
				_DFS(pCur->_dst, visited);
			pCur = pCur->_pNext;
		}
	}

二、最小生成树

连通图中的每一棵生成树，都是原图的一个极大无环子图，即：从其中删去任何一条边，生成树就不在连通；反之，在其中引入任何一条新边，都会形成一条回路。
若连通图由n个顶点组成，则其生成树必含n个顶点和n-1条边。因此构造最小生成树的准则有三 条：
（1）. 只能使用图中的边来构造最小生成树

（2）. 只能使用恰好n-1条边来连接图中的n个顶点

（3）. 选用的n-1条边不能构成回路
构造最小生成树的方法：Kruskal算法和Prim算法。这两个算法都采用了逐步求解的贪心策略。
注：贪心算法：是指在问题求解时，总是做出当前看起来最好的选择。也就是说贪心算法做出的不是整体最优的的选择，而是某种意义上的局部最优解。贪心算法不是对所有的问题都能得到整体最优解。

我们了解一下两种算法。

1、Kruskal算法

 任给一个有n个顶点的连通网络N={V, E}，首先构造一个由这n个顶点组成、不含任何边的图G= {V, NU LL }，其中每个顶点自成一个连通分量，不断从E中取出权值最小的一条边(若有多条任取其一) ，若该边的两个顶点来自不同的连通分量，则将此边加入到G中。如此重复，直到所有顶点在同一个连通分量上为止。

核心：每次迭代时，选出一条具有最小权值，且两端点不在同一连通分量上的边，加入生成树。

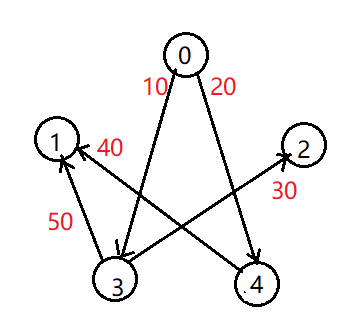
举例说明一下：

步骤如下：

（1）新建一个图，只有图的顶点，没有边，且 我们有5个顶点，因此需要4（n-1)条边

（2）将原图中边的权值，从小到大排序

（3）利用之前写过的 并查集，如果需要连接的顶点不在已经连通的集合里，那么将该边加到新图中；

       否则，继续看下一条边。 

可以参考之前文章的并查集。

具体实现：

// 最小生成树---克鲁斯卡尔算法；
	typedef Graph Self;
	typedef Node LinkEdge;
	Self Kruskal()
	{
		Self g;  //新建一个图
		g._v = _v; //
		g._linkEdges.resize(_v.size());
		vector edges;

		for (size_t i = 0; i > _v.size(); i++)
		{
			LinkEdge* pCur = _linkEdges[i];
			while (pCur)
			{
				if (IsDirect || (!IsDirect&&pCur->_src < pCur->_dst))  //保存边的权值
					edges.push_back(pCur);
				pCur = pCur->_pNext;
			}
		}
		class Compare
		{
		public:
			bool operator()(const LinkEdge* left, const LinkEdge* right)
			{
				return left->_weight < right->_weight;
			}
		};

		sort(edges.begin(), edges.end(), Compare());

		size_t count = _v.size() - 1;//从前往后取n-1条边
		UnionFind u(_v.size());
		for (size_t i = 0; i < edges.size(); i++)
		{
			LinkEdge* pCur = edges[i];
			size_t srcRoot = u.FindRoot(pCur->_src);
			size_t dstRoot = u.FindRoot(pCur->_dst);
			if (srcRoot != dstRoot)  //两个节点不在一个集合，加边
			{
				g.AddEdge(pCur->_src, pCur->_dst, pCur->_weight);
				if (!IsDirect)        //有向图
					g.AddEdge(pCur->_dst, pCur->_src, pCur->_weight);

				u.Union(pCur->_src, pCur->_dst);//合并
				count--;

				if (count == 0)
					break;
			}
		}
		if (count > 0)
			cout << "最小生成树非法" << endl;
		return g;
	}

2、Prim算法

普里姆算法 （Prim算法），图论中的一种算法，可在加权连通图里搜索 最小生成树 。

即由此算法搜索到的边子集所构成的树中，不但包括了连通图里的所有顶点，且其所有边的权值之和亦为最小。该算法于1930年由捷克数学家沃伊捷赫·亚尔尼克（英语：Vojtěch Jarník）发现；并在1957年由美国计算机科学家罗伯特·普里姆（英语：Robert C. Prim）独立发现；1959年， 艾兹格·迪科斯彻 再次发现了该算法。因此，在某些场合，普里姆算法又被称为DJP算法、亚尔尼克算法或普里姆－亚尔尼克算法。

1).输入：一个加权连通图，其中顶点集合为V，边集合为E；

2).初始化：V _new = {x}，其中x为集合V中的任一节点（起始点），E _new = {},为空；

3).重复下列操作，直到V _new = V。

   a.在集合E中选取权值最小的边，其中u为集合V _new中的元素，而v不在V _new 集合当中，并且v∈V（如果存在有多条满足前  述条件即具有相同权值的边，则可任意选取其中之一）；

    b.将v加入集合V _new中，将边加入集合E _new中；

4).输出：使用集合V _new和E _new来描述所得到的 最小生成树。