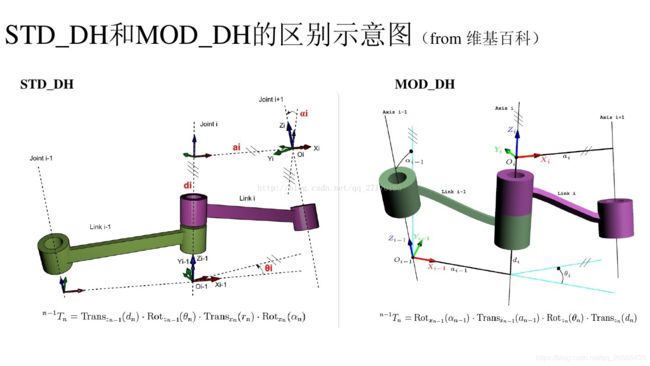
机器人学回炉重造（1）：正运动学、标准D-H法与改进D-H法的区别与应用（附ABB机械臂运动学建模matlab代码）
写在前面
书读百遍，其义自见。
要想当一名合格的机器人工程师，机器人学就是base_link，看多少遍都不为过。现在回炉重造一下，记录一下学习笔记（以照片形式，打公式太费劲了），防止以后笔记本不见了。
正运动学
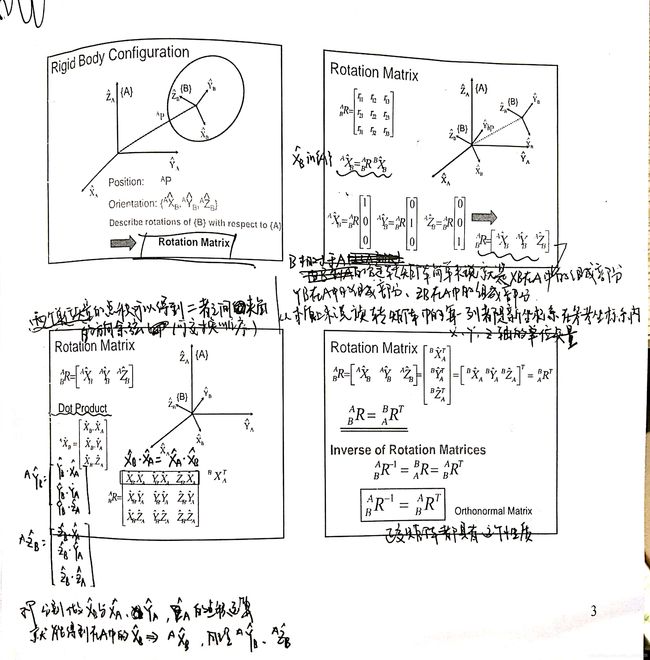
首先是旋转矩阵的理解。
在理解旋转矩阵的基础之上，理解一些姿态的表现方式，例如欧拉角等。
然后进入最基本的工作，计算正运动学。正运动学就是根据关节角度，计算机器人工具坐标系（末端执行器end_effector）在机器人基座标系（base_link）下的位姿。
D-H建模方法
我这里只介绍一种，Modified D-H法，即改进D-H参数法，另外还有标准D-H参数法，我就不做笔记了。
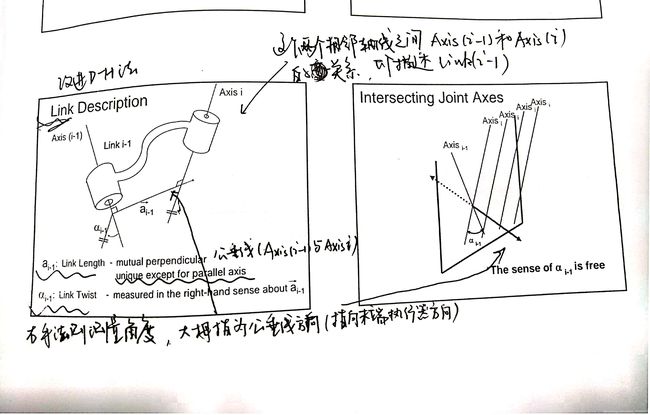
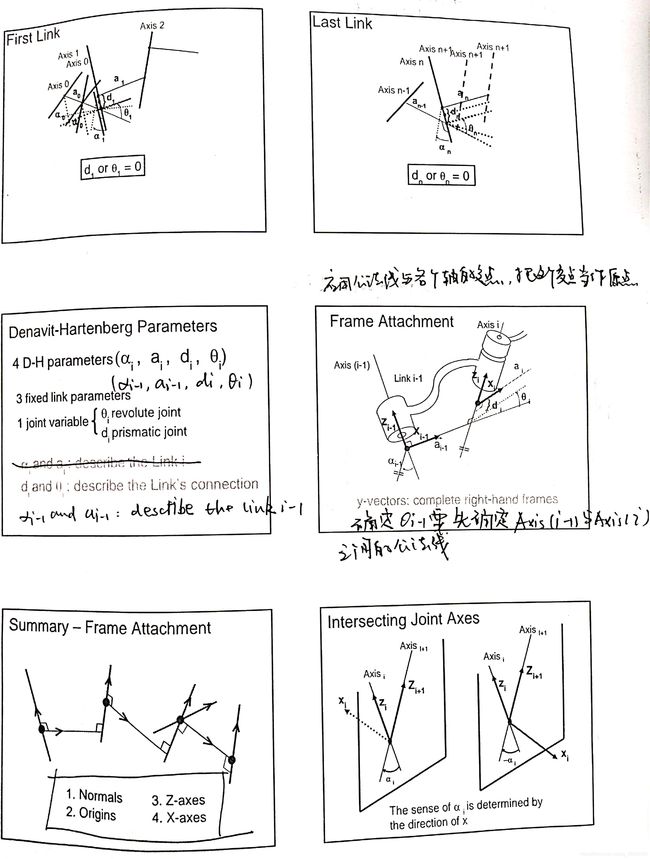
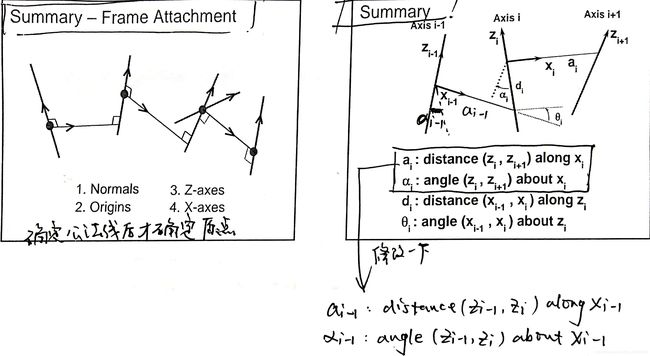
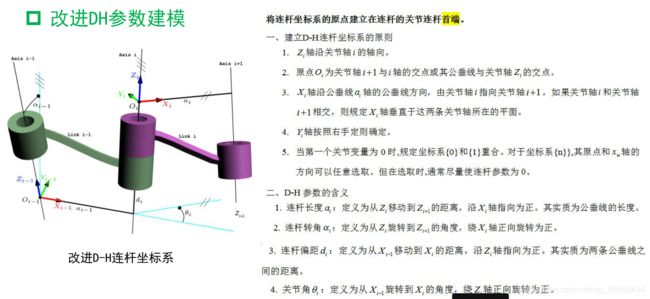
总结改进D-H参数法建立的基本顺序及四个参数的具体定义。
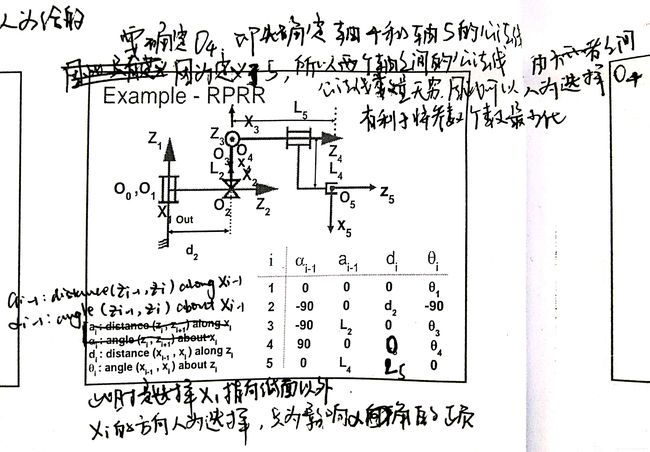
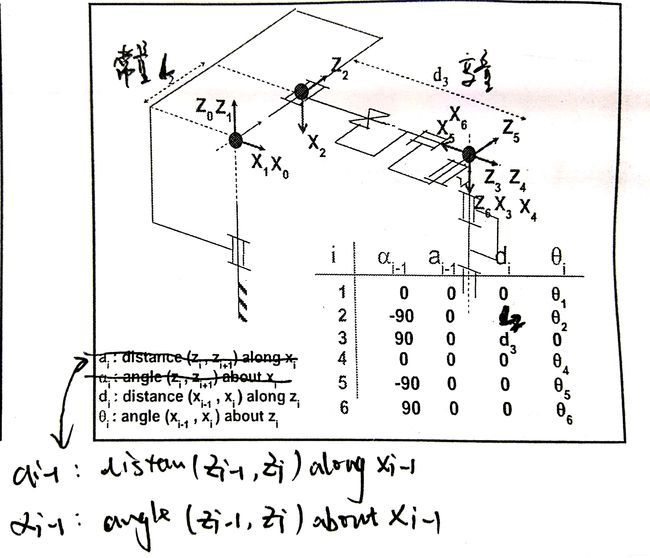
两个简单的例子。Xi在Zi-1和Zi的公法线上，方向人为选择，最终只会影响α角的正负。
实例
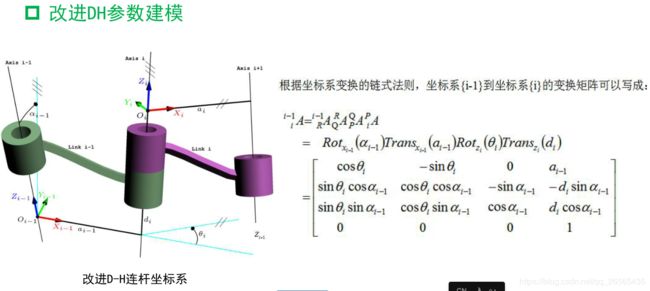
建立改进D-H坐标系
以ABB一款机械臂为例，采用改进D-H参数法。该机械臂6个关节都是转动关节，前3个关节确定手腕参考点的位置，后3个关节确定手腕的方位。和大多数工业机器人一样，后3个关节轴线交于一点，因此将该点作为手腕的参考点，也选作为连杆坐标系{4},{5}和{6}的原点。在改进D-H坐标系中，{0}和{1}一般重合，O1为轴1和轴2公法线在轴1上的交点，此时关节1和关节2在z方向上的偏置没有体现出来，对于整个机械臂各关节的相对运动来说并没有影响。
先建立改进D-H坐标系如下
改进D-H参数表
根据坐标系和上文提到的各个参数量的具体定义，填写D-H参数表如下
| i | αi-1 | ai-1 | di | θi |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | θ1 |
| 2 | pi/2 | L1=320 | 0 | θ2 |
| 3 | 0 | L3=975 | 0 | θ3 |
| 4 | pi/2 | L5=200 | L6=887 | θ4 |
| 5 | -pi/2 | 0 | 0 | θ5 |
| 6 | pi/2 | 0 | 0 | θ6 |
Matlab仿真程序（Modified DH）
% Modified DH
% ABB robot
clear;
clc;
th(1) = 0; d(1) = 0; a(1) = 0; alp(1) = 0;
th(2) = 0; d(2) = 0; a(2) = 0.320; alp(2) = pi/2;
th(3) = 0; d(3) = 0; a(3) = 0.975; alp(3) = 0;
th(4) = 0; d(4) = 0.887; a(4) = 0.2; alp(4) = pi/2;
th(5) = 0; d(5) = 0; a(5) = 0; alp(5) = -pi/2;
th(6) = 0; d(6) = 0; a(6) = 0; alp(6) = pi/2;
% DH parameters th d a alpha sigma
L1 = Link([th(1), d(1), a(1), alp(1), 0], 'modified');
L2 = Link([th(2), d(2), a(2), alp(2), 0], 'modified');
L3 = Link([th(3), d(3), a(3), alp(3), 0], 'modified');
L4 = Link([th(4), d(4), a(4), alp(4), 0], 'modified');
L5 = Link([th(5), d(5), a(5), alp(5), 0], 'modified');
L6 = Link([th(6), d(6), a(6), alp(6), 0], 'modified');
robot = SerialLink([L1, L2, L3, L4, L5, L6]);
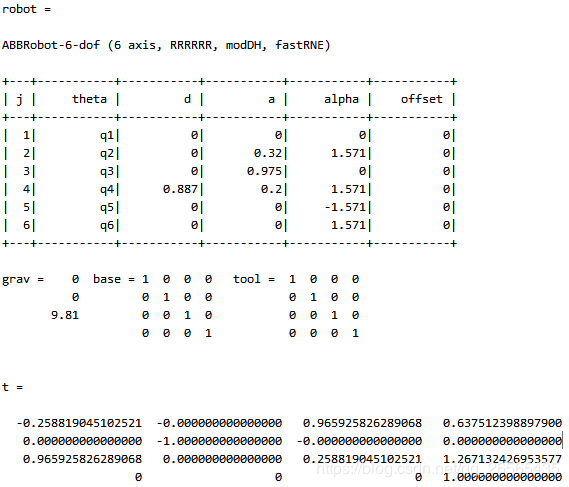
robot.name='ABBRobot-6-dof';
robot.display()
% Forward Pose Kinematics
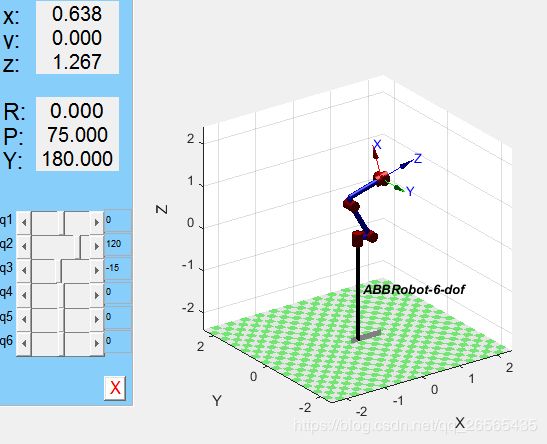
theta = [0, 120, -15, 0, 0, 0]*pi/180;
robot.teach();
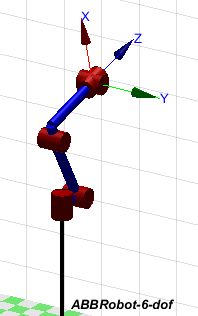
robot.plot(theta);
t0 = robot.fkine(theta) %末端执行器位姿
运行结果
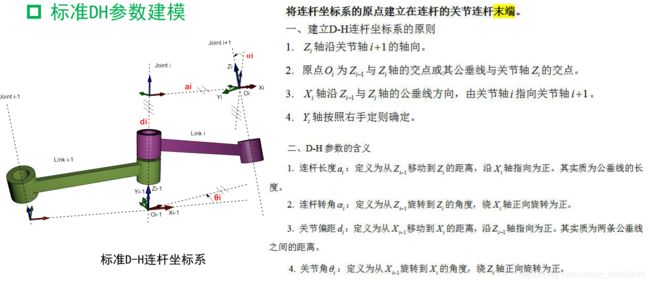
建立标准D-H坐标系
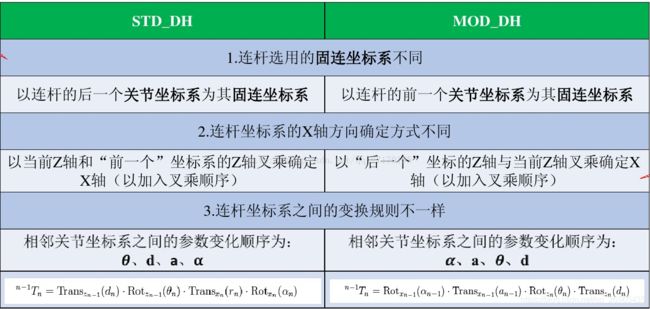
和改进D-H参数法不同的是：
- 改进D-H参数法α和a的下标均为i-1，而标准D-H中两个参数的下标均为i；
- 改进D-H中Xi是Zi和Zi+1的公垂线，而在标准D-H中Xi是Zi-1和Zi的公垂线；
- 在使用两种方法时，一般先使各θi角为0进行建模；
- 标准D-H中各参数定义如下：
- αi angle(Zi-1, Zi)about Xi
- ai distance ({i-1}, {i} origin) along Xi-1
- di distance (Xi-1, Xi) along Zi-1
- θi angle (Xi-1, Xi) about Zi-1
建立标准D-H坐标系如下
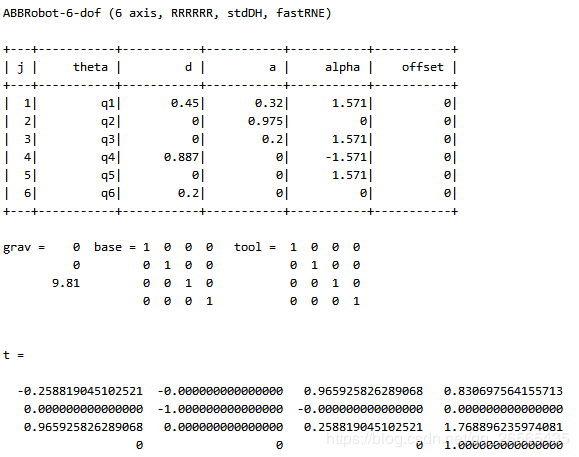
标准D-H参数表
| i | αi | ai | di | θi |
|---|---|---|---|---|
| 1 | pi/2 | 0.320 | 0.450 | θ1 |
| 2 | 0 | 0.975 | 0 | θ2 |
| 3 | pi/2 | 0.200 | 0 | θ3 |
| 4 | -pi/2 | 0 | 0.887 | θ4 |
| 5 | pi/2 | 0 | 0 | θ5 |
| 6 | 0 | 0 | 0.200 | θ6 |
Matlab仿真程序（Standard D-H）
% Standard DH
% ABB robot
clear;
clc;
th(1) = 0; d(1) = 0.450; a(1) = 0.320; alp(1) = pi/2;
th(2) = 0; d(2) = 0; a(2) = 0.975; alp(2) = 0;
th(3) = 0; d(3) = 0; a(3) = 0.200; alp(3) = pi/2;
th(4) = 0; d(4) = 0.887; a(4) = 0; alp(4) = -pi/2;
th(5) = 0; d(5) = 0; a(5) = 0; alp(5) = pi/2;
th(6) = 0; d(6) = 0.200; a(6) = 0; alp(6) = 0;
% DH parameters th d a alpha sigma
L1 = Link([th(1), d(1), a(1), alp(1), 0]);
L2 = Link([th(2), d(2), a(2), alp(2), 0]);
L3 = Link([th(3), d(3), a(3), alp(3), 0]);
L4 = Link([th(4), d(4), a(4), alp(4), 0]);
L5 = Link([th(5), d(5), a(5), alp(5), 0]);
L6 = Link([th(6), d(6), a(6), alp(6), 0]);
robot = SerialLink([L1, L2, L3, L4, L5, L6]);
robot.name='ABBRobot-6-dof';
robot.display()
theta = [0, 120, -15, 0, 0, 0]*pi/180;
robot.teach();
robot.plot(theta);
t = robot.fkine(theta) %末端执行器位姿
运行结果
从两个方法的末端姿态计算结果可以看出，不完全一致，这是因为两个方法的基座标位置不一样，并且改进dh法建模坐标系{6}没有建到工具坐标系上，而是在手腕位置，而标准dh法则是建到了末端工具坐标系上，这也就直接导致在[0 0 0 0 0 0]末端姿态的pz不一样，转换关系为0.887-0.45+0.2=0.637。
