数据结构(六)——图之最小生成树Prim和Kruskal算法
代码中所用到的结构体
typedef struct arcnode
{
int weight;//边的权重
int adjvex;//指向的下一个顶点
struct arcnode *next;//指向这个点的另一条边
}Arcnode,*pArcnode;
typedef struct vnode
{
pArcnode firstarc;//点所指向的第一条边
}Vnode,AdjList[30];
typedef struct graph
{
int Vnum,Arcnum;//点的数目,边的数目
AdjList vertice;
}Graph,*pGraph;
typedef struct edges
{
int begin;//边的一个端点
int end;//边的另一个端点
int weight;//边的权重
}Edges;
typedef struct closedge
{
int adjvex;//最小边的起始点
int lowcost;//最小边的权重
}Closedge[50];
构造无向图
void CreateGraph(pGraph G,Edges E[])//构造无向图
{
int i;
int node1,node2,weight;//暂时存储数据
pArcnode p1,p2;//两个有向边组成一个无向边
printf("请输入无向图的总点数:\n");
scanf("%d",&G->Vnum);
getchar();
for(i=0;i<G->Vnum;i++)//给每个结点的第一个后继边初始化
{
G->vertice[i].firstarc=NULL;
}
printf("请输入无向图的总边数:\n");
scanf("%d",&G->Arcnum);
getchar();
printf("请输入点和点之间的连接及其权重:(例:1 5 10)\n");
for(i=0;i<G->Arcnum;i++)//循环输入边的信息
{
scanf("%d %d %d",&node1,&node2,&weight);
getchar();
E[i].begin=node1;
E[i].end=node2;
E[i].weight=weight;
p1=(pArcnode)malloc(sizeof(Arcnode));
p2=(pArcnode)malloc(sizeof(Arcnode));
p1->adjvex=node1;//构造连接,即两个有向边组成一个无向边
p1->weight=weight;
p1->next=NULL;
p2->adjvex=node2;
p2->weight=weight;
p2->next=NULL;
if(G->vertice[node1].firstarc==NULL&&G->vertice[node1].firstarc==NULL)//还未有邻接点时
{
G->vertice[node2].firstarc=p1;
G->vertice[node1].firstarc=p2;
}
else//已有邻接点时
{
p1->next=G->vertice[node2].firstarc;
G->vertice[node2].firstarc=p1;
p2->next=G->vertice[node1].firstarc;
G->vertice[node1].firstarc=p2;
}
}
}
Prim算法
算法思想
- 在无向图中选取一个点 pos
- 遍历 pos 点的所有邻接边
- 将该点加入集合U(即标记该点遍历过),在其所有邻接边中选取最小的那条边,将 pos 的值改为该边指向的那个点的位置,并打印第一条边。
- 重复第二个操作和第三个操作,直到所有点都并入生成树。
代码中的重要参数 - min:记录U到U-V之间最小边的权值
- minid:记录最小边的终点,即在U-V集合的点
- pos:记录刚刚进入U集合的新点的位置
- C:记录最短边的结构体数组,记录了最短边的起始点(即在U中的点),最小边的权重。
void Prim(pGraph G)//构造最小生成树
{
int i,j;
int min=MAX,minid=0,pos;//min,minid为记录U和V-U之间的最短边的大小及其终点,pos用于记录进入U的新点的位置
Closedge C;//最短边集合
Arcnode *p;
for(i=0;i<G->Vnum;i++)//对最短边数组初始化
{
C[i].lowcost=MAX;//不连通时赋值为MAX
C[i].adjvex=0;
}
pos=0;//假设均是从pos==0处开始构造图的
C[pos].lowcost=0;//lowcost==0表示该点已经并入U集合
for(i=1;i<G->Vnum;i++)//构造最小生成树需要进行n-1次循环
{
p=G->vertice[pos].firstarc;//得到当前点的第一条边
while(p!=NULL)//遍历完该点连接的所有边
{
if(C[p->adjvex].lowcost>p->weight)//当该点连接的边的边的权重小于已有的记录,进行数据更新
{
C[p->adjvex].lowcost=p->weight;//更新U到V-U的最短距离
C[p->adjvex].adjvex=pos;//更新最短点的起始点
}
p=p->next;
}
for(j=0;j<G->Vnum;j++)//寻找lowcost中最小的边
{
if(min>C[j].lowcost&&C[j].lowcost!=0)//判断是否为最小边
{
min=C[j].lowcost;
minid=j;
}
}
printf("%d-%d:%d\n",C[minid].adjvex,minid,min);//打印最小生成树中的一边
C[minid].lowcost=0;//将该点并入U
pos=minid;//更新下一个要作为源点进行更新的点
min=MAX;//初始化min
}
}
Kruskal算法
算法思想
- 和Prim算法不同,Prim算法是以点为基础,来构造最小生成树,而Kruskal算法是以边为基础来构造最小生成树。
- 首先选取当前图中权值最小的边,判断其并入生成树后是否会构成回路,若不会,则将其并入回路;否则,将其寻找下一个次小的。
- 重复第二个步骤,直到图生成了最小生成树。
Findroot函数 - 重要参数:parent【】存储当前结点在生成树中的父亲节点。
- 返回值为树根。
- 目的:为后面判断加入改边是否构成回路做铺垫。
int Findroot(int parent[],int m)
{
while(parent[m]>=0)
{
m=parent[m];
}
return m;
}
Kruskal函数
- 重要参数:parent【】,用于存储每个点在生成树中的父亲结点;Edges【】,存储边的两个端点,权重;
void Kruskal(pGraph G,Edges E[])//寻找最小生成树
{
int parent[G->Vnum];//用于存储每个点在生成树中的父亲结点
int n,m;
int i,j;
for(i=0;i<G->Vnum;i++)//初始化
{
parent[i]=-1;
}
for(i=0;i<G->Arcnum;i++)//两个for循环实现对边的权重的冒泡排序
{
for(j=0;j<G->Arcnum-1;j++)
{
if(E[j].weight>E[j+1].weight)
{
swap(&E[j].begin,&E[j+1].begin);
swap(&E[j].end,&E[j+1].end);
swap(&E[j].weight,&E[j+1].weight);
}
}
}
for(i=0;i<G->Arcnum;i++)//判断加入该边是否构成环
{
n=Findroot(parent,E[i].begin);//获得树根
m=Findroot(parent,E[i].end);//获得树根
if(n!=m)//判断树根是否相等,若相等,则加入该边一定会构成环
{
parent[n]=m;
printf("%d-%d:%d\n",E[i].begin,E[i].end,E[i].weight);
}
}
}
源代码
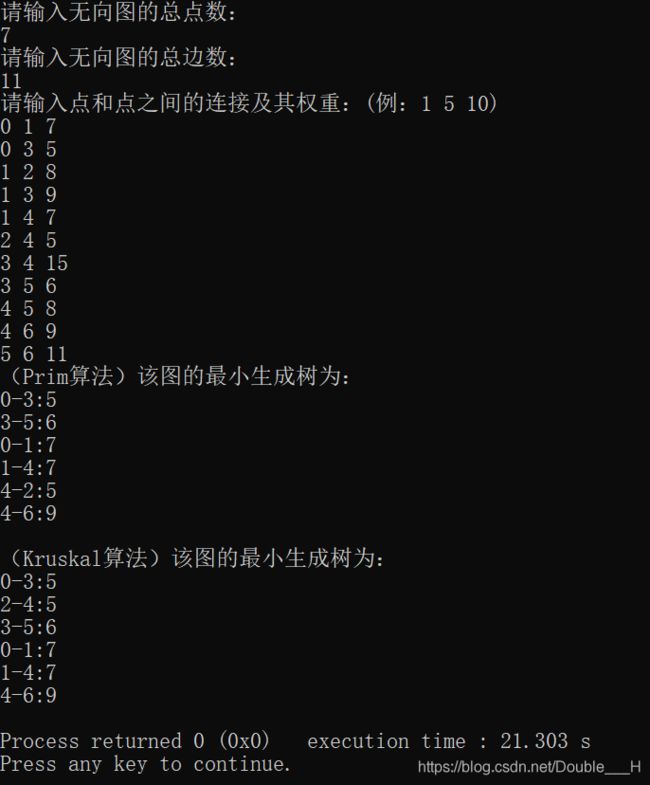
#include 测试样例:
7
11
0 1 7
0 3 5
1 2 8
1 3 9
1 4 7
2 4 5
3 4 15
3 5 6
4 5 8
4 6 9
5 6 11
结果截图